Martin Wainwright
SAFFRON: an adaptive algorithm for online control of the false discovery rate
Feb 25, 2018



Abstract:In the online false discovery rate (FDR) problem, one observes a possibly infinite sequence of $p$-values $P_1,P_2,\dots$, each testing a different null hypothesis, and an algorithm must pick a sequence of rejection thresholds $\alpha_1,\alpha_2,\dots$ in an online fashion, effectively rejecting the $k$-th null hypothesis whenever $P_k \leq \alpha_k$. Importantly, $\alpha_k$ must be a function of the past, and cannot depend on $P_k$ or any of the later unseen $p$-values, and must be chosen to guarantee that for any time $t$, the FDR up to time $t$ is less than some pre-determined quantity $\alpha \in (0,1)$. In this work, we present a powerful new framework for online FDR control that we refer to as SAFFRON. Like older alpha-investing (AI) algorithms, SAFFRON starts off with an error budget, called alpha-wealth, that it intelligently allocates to different tests over time, earning back some wealth on making a new discovery. However, unlike older methods, SAFFRON's threshold sequence is based on a novel estimate of the alpha fraction that it allocates to true null hypotheses. In the offline setting, algorithms that employ an estimate of the proportion of true nulls are called adaptive methods, and SAFFRON can be seen as an online analogue of the famous offline Storey-BH adaptive procedure. Just as Storey-BH is typically more powerful than the Benjamini-Hochberg (BH) procedure under independence, we demonstrate that SAFFRON is also more powerful than its non-adaptive counterparts, such as LORD and other generalized alpha-investing algorithms. Further, a monotone version of the original AI algorithm is recovered as a special case of SAFFRON, that is often more stable and powerful than the original. Lastly, the derivation of SAFFRON provides a novel template for deriving new online FDR rules.
When is it Better to Compare than to Score?
Jun 25, 2014


Abstract:When eliciting judgements from humans for an unknown quantity, one often has the choice of making direct-scoring (cardinal) or comparative (ordinal) measurements. In this paper we study the relative merits of either choice, providing empirical and theoretical guidelines for the selection of a measurement scheme. We provide empirical evidence based on experiments on Amazon Mechanical Turk that in a variety of tasks, (pairwise-comparative) ordinal measurements have lower per sample noise and are typically faster to elicit than cardinal ones. Ordinal measurements however typically provide less information. We then consider the popular Thurstone and Bradley-Terry-Luce (BTL) models for ordinal measurements and characterize the minimax error rates for estimating the unknown quantity. We compare these minimax error rates to those under cardinal measurement models and quantify for what noise levels ordinal measurements are better. Finally, we revisit the data collected from our experiments and show that fitting these models confirms this prediction: for tasks where the noise in ordinal measurements is sufficiently low, the ordinal approach results in smaller errors in the estimation.
Comunication-Efficient Algorithms for Statistical Optimization
Oct 11, 2013
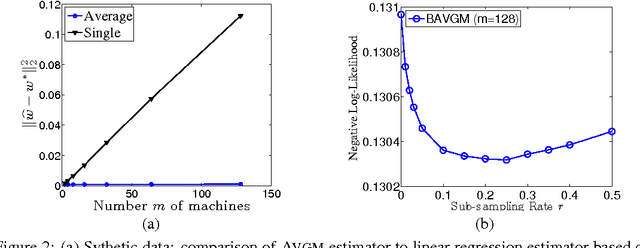

Abstract:We analyze two communication-efficient algorithms for distributed statistical optimization on large-scale data sets. The first algorithm is a standard averaging method that distributes the $N$ data samples evenly to $\nummac$ machines, performs separate minimization on each subset, and then averages the estimates. We provide a sharp analysis of this average mixture algorithm, showing that under a reasonable set of conditions, the combined parameter achieves mean-squared error that decays as $\order(N^{-1}+(N/m)^{-2})$. Whenever $m \le \sqrt{N}$, this guarantee matches the best possible rate achievable by a centralized algorithm having access to all $\totalnumobs$ samples. The second algorithm is a novel method, based on an appropriate form of bootstrap subsampling. Requiring only a single round of communication, it has mean-squared error that decays as $\order(N^{-1} + (N/m)^{-3})$, and so is more robust to the amount of parallelization. In addition, we show that a stochastic gradient-based method attains mean-squared error decaying as $O(N^{-1} + (N/ m)^{-3/2})$, easing computation at the expense of penalties in the rate of convergence. We also provide experimental evaluation of our methods, investigating their performance both on simulated data and on a large-scale regression problem from the internet search domain. In particular, we show that our methods can be used to efficiently solve an advertisement prediction problem from the Chinese SoSo Search Engine, which involves logistic regression with $N \approx 2.4 \times 10^8$ samples and $d \approx 740,000$ covariates.
A New Class of Upper Bounds on the Log Partition Function
Dec 12, 2012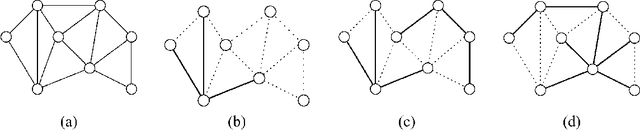


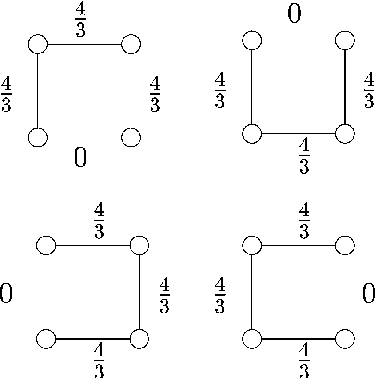
Abstract:Bounds on the log partition function are important in a variety of contexts, including approximate inference, model fitting, decision theory, and large deviations analysis. We introduce a new class of upper bounds on the log partition function, based on convex combinations of distributions in the exponential domain, that is applicable to an arbitrary undirected graphical model. In the special case of convex combinations of tree-structured distributions, we obtain a family of variational problems, similar to the Bethe free energy, but distinguished by the following desirable properties: i. they are cnvex, and have a unique global minimum; and ii. the global minimum gives an upper bound on the log partition function. The global minimum is defined by stationary conditions very similar to those defining fixed points of belief propagation or tree-based reparameterization Wainwright et al., 2001. As with BP fixed points, the elements of the minimizing argument can be used as approximations to the marginals of the original model. The analysis described here can be extended to structures of higher treewidth e.g., hypertrees, thereby making connections with more advanced approximations e.g., Kikuchi and variants Yedidia et al., 2001; Minka, 2001.
On the optimality of tree-reweighted max-product message-passing
Jul 04, 2012

Abstract:Tree-reweighted max-product (TRW) message passing is a modified form of the ordinary max-product algorithm for attempting to find minimal energy configurations in Markov random field with cycles. For a TRW fixed point satisfying the strong tree agreement condition, the algorithm outputs a configuration that is provably optimal. In this paper, we focus on the case of binary variables with pairwise couplings, and establish stronger properties of TRW fixed points that satisfy only the milder condition of weak tree agreement (WTA). First, we demonstrate how it is possible to identify part of the optimal solution|i.e., a provably optimal solution for a subset of nodes| without knowing a complete solution. Second, we show that for submodular functions, a WTA fixed point always yields a globally optimal solution. We establish that for binary variables, any WTA fixed point always achieves the global maximum of the linear programming relaxation underlying the TRW method.
Dual Averaging for Distributed Optimization: Convergence Analysis and Network Scaling
Apr 10, 2011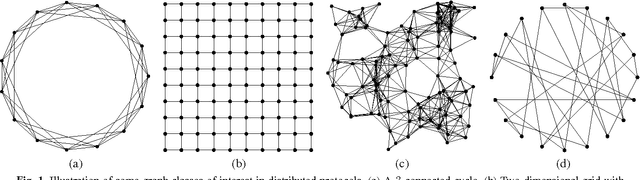
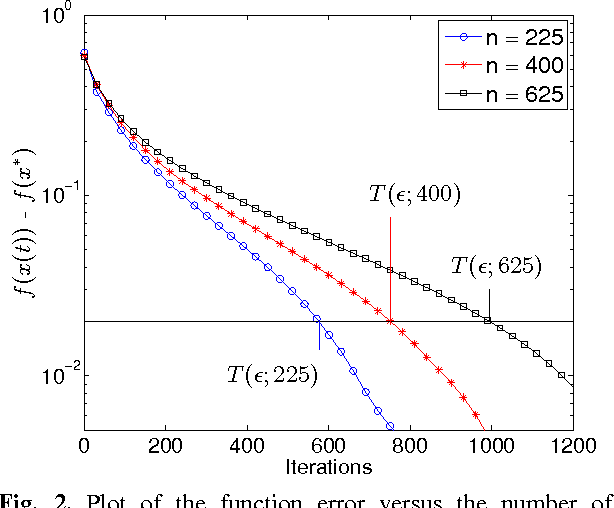
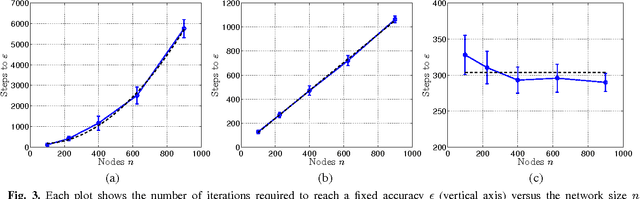

Abstract:The goal of decentralized optimization over a network is to optimize a global objective formed by a sum of local (possibly nonsmooth) convex functions using only local computation and communication. It arises in various application domains, including distributed tracking and localization, multi-agent co-ordination, estimation in sensor networks, and large-scale optimization in machine learning. We develop and analyze distributed algorithms based on dual averaging of subgradients, and we provide sharp bounds on their convergence rates as a function of the network size and topology. Our method of analysis allows for a clear separation between the convergence of the optimization algorithm itself and the effects of communication constraints arising from the network structure. In particular, we show that the number of iterations required by our algorithm scales inversely in the spectral gap of the network. The sharpness of this prediction is confirmed both by theoretical lower bounds and simulations for various networks. Our approach includes both the cases of deterministic optimization and communication, as well as problems with stochastic optimization and/or communication.
* 40 pages, 4 figures
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge