SAFFRON: an adaptive algorithm for online control of the false discovery rate
Paper and Code
Feb 25, 2018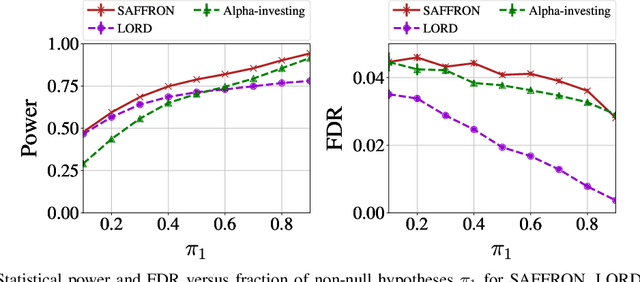
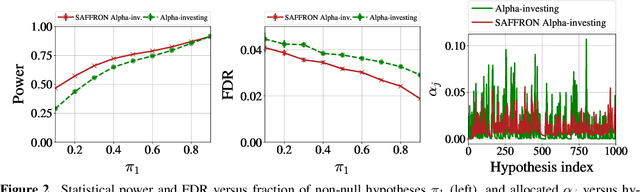
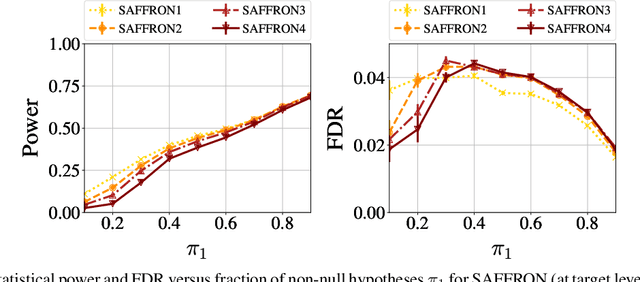
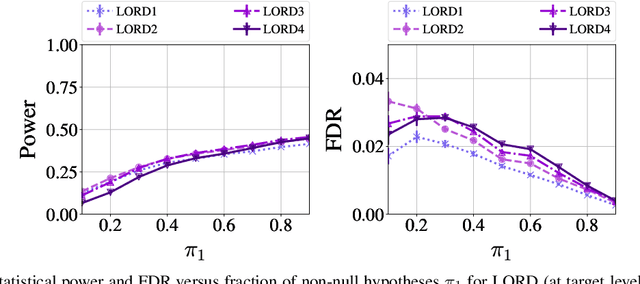
In the online false discovery rate (FDR) problem, one observes a possibly infinite sequence of $p$-values $P_1,P_2,\dots$, each testing a different null hypothesis, and an algorithm must pick a sequence of rejection thresholds $\alpha_1,\alpha_2,\dots$ in an online fashion, effectively rejecting the $k$-th null hypothesis whenever $P_k \leq \alpha_k$. Importantly, $\alpha_k$ must be a function of the past, and cannot depend on $P_k$ or any of the later unseen $p$-values, and must be chosen to guarantee that for any time $t$, the FDR up to time $t$ is less than some pre-determined quantity $\alpha \in (0,1)$. In this work, we present a powerful new framework for online FDR control that we refer to as SAFFRON. Like older alpha-investing (AI) algorithms, SAFFRON starts off with an error budget, called alpha-wealth, that it intelligently allocates to different tests over time, earning back some wealth on making a new discovery. However, unlike older methods, SAFFRON's threshold sequence is based on a novel estimate of the alpha fraction that it allocates to true null hypotheses. In the offline setting, algorithms that employ an estimate of the proportion of true nulls are called adaptive methods, and SAFFRON can be seen as an online analogue of the famous offline Storey-BH adaptive procedure. Just as Storey-BH is typically more powerful than the Benjamini-Hochberg (BH) procedure under independence, we demonstrate that SAFFRON is also more powerful than its non-adaptive counterparts, such as LORD and other generalized alpha-investing algorithms. Further, a monotone version of the original AI algorithm is recovered as a special case of SAFFRON, that is often more stable and powerful than the original. Lastly, the derivation of SAFFRON provides a novel template for deriving new online FDR rules.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge