A Compositional Kernel Model for Feature Learning

We study a compositional variant of kernel ridge regression in which the predictor is applied to a coordinate-wise reweighting of the inputs. Formulated as a variational problem, this model provides a simple testbed for feature learning in compositional architectures. From the perspective of variable selection, we show how relevant variables are recovered while noise variables are eliminated. We establish guarantees showing that both global minimizers and stationary points discard noise coordinates when the noise variables are Gaussian distributed. A central finding is that $\ell_1$-type kernels, such as the Laplace kernel, succeed in recovering features contributing to nonlinear effects at stationary points, whereas Gaussian kernels recover only linear ones.

Learning Variational Inequalities from Data: Fast Generalization Rates under Strong Monotonicity

Variational inequalities (VIs) are a broad class of optimization problems encompassing machine learning problems ranging from standard convex minimization to more complex scenarios like min-max optimization and computing the equilibria of multi-player games. In convex optimization, strong convexity allows for fast statistical learning rates requiring only $\Theta(1/\epsilon)$ stochastic first-order oracle calls to find an $\epsilon$-optimal solution, rather than the standard $\Theta(1/\epsilon^2)$ calls. In this paper, we explain how one can similarly obtain fast $\Theta(1/\epsilon)$ rates for learning VIs that satisfy strong monotonicity, a generalization of strong convexity. Specifically, we demonstrate that standard stability-based generalization arguments for convex minimization extend directly to VIs when the domain admits a small covering, or when the operator is integrable and suboptimality is measured by potential functions; such as when finding equilibria in multi-player games.

Data Acquisition via Experimental Design for Decentralized Data Markets

Acquiring high-quality training data is essential for current machine learning models. Data markets provide a way to increase the supply of data, particularly in data-scarce domains such as healthcare, by incentivizing potential data sellers to join the market. A major challenge for a data buyer in such a market is selecting the most valuable data points from a data seller. Unlike prior work in data valuation, which assumes centralized data access, we propose a federated approach to the data selection problem that is inspired by linear experimental design. Our proposed data selection method achieves lower prediction error without requiring labeled validation data and can be optimized in a fast and federated procedure. The key insight of our work is that a method that directly estimates the benefit of acquiring data for test set prediction is particularly compatible with a decentralized market setting.

Chatbot Arena: An Open Platform for Evaluating LLMs by Human Preference

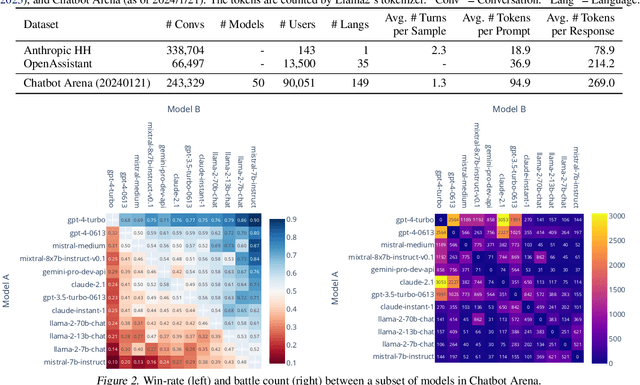
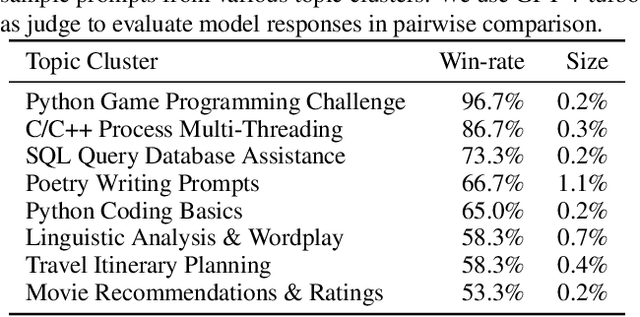
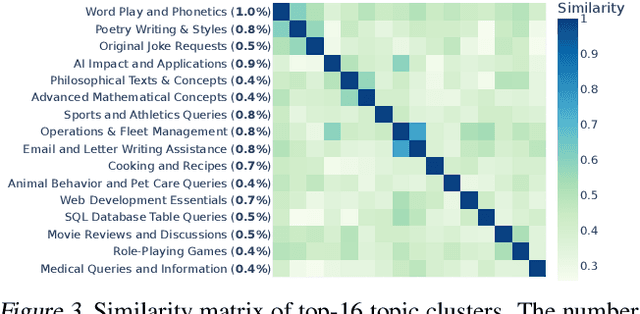
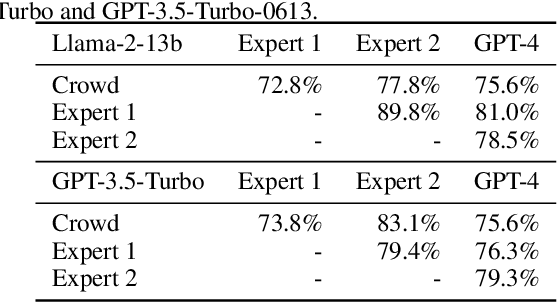
Large Language Models (LLMs) have unlocked new capabilities and applications; however, evaluating the alignment with human preferences still poses significant challenges. To address this issue, we introduce Chatbot Arena, an open platform for evaluating LLMs based on human preferences. Our methodology employs a pairwise comparison approach and leverages input from a diverse user base through crowdsourcing. The platform has been operational for several months, amassing over 240K votes. This paper describes the platform, analyzes the data we have collected so far, and explains the tried-and-true statistical methods we are using for efficient and accurate evaluation and ranking of models. We confirm that the crowdsourced questions are sufficiently diverse and discriminating and that the crowdsourced human votes are in good agreement with those of expert raters. These analyses collectively establish a robust foundation for the credibility of Chatbot Arena. Because of its unique value and openness, Chatbot Arena has emerged as one of the most referenced LLM leaderboards, widely cited by leading LLM developers and companies. Our demo is publicly available at \url{https://chat.lmsys.org}.

Classifier Calibration with ROC-Regularized Isotonic Regression

Calibration of machine learning classifiers is necessary to obtain reliable and interpretable predictions, bridging the gap between model confidence and actual probabilities. One prominent technique, isotonic regression (IR), aims at calibrating binary classifiers by minimizing the cross entropy on a calibration set via monotone transformations. IR acts as an adaptive binning procedure, which allows achieving a calibration error of zero, but leaves open the issue of the effect on performance. In this paper, we first prove that IR preserves the convex hull of the ROC curve -- an essential performance metric for binary classifiers. This ensures that a classifier is calibrated while controlling for overfitting of the calibration set. We then present a novel generalization of isotonic regression to accommodate classifiers with K classes. Our method constructs a multidimensional adaptive binning scheme on the probability simplex, again achieving a multi-class calibration error equal to zero. We regularize this algorithm by imposing a form of monotony that preserves the K-dimensional ROC surface of the classifier. We show empirically that this general monotony criterion is effective in striking a balance between reducing cross entropy loss and avoiding overfitting of the calibration set.

Provably Personalized and Robust Federated Learning

Clustering clients with similar objectives and learning a model per cluster is an intuitive and interpretable approach to personalization in federated learning. However, doing so with provable and optimal guarantees has remained an open challenge. In this work, we formalize personalized federated learning as a stochastic optimization problem where the stochastic gradients on a client may correspond to one of $K$ distributions. In such a setting, we show that using i) a simple thresholding-based clustering algorithm, and ii) local client gradients obtains optimal convergence guarantees. In fact, our rates asymptotically match those obtained if we knew the true underlying clustering of the clients. Furthermore, our algorithms are provably robust in the Byzantine setting where some fraction of the gradients are corrupted.

Doubly Robust Self-Training

Self-training is an important technique for solving semi-supervised learning problems. It leverages unlabeled data by generating pseudo-labels and combining them with a limited labeled dataset for training. The effectiveness of self-training heavily relies on the accuracy of these pseudo-labels. In this paper, we introduce doubly robust self-training, a novel semi-supervised algorithm that provably balances between two extremes. When the pseudo-labels are entirely incorrect, our method reduces to a training process solely using labeled data. Conversely, when the pseudo-labels are completely accurate, our method transforms into a training process utilizing all pseudo-labeled data and labeled data, thus increasing the effective sample size. Through empirical evaluations on both the ImageNet dataset for image classification and the nuScenes autonomous driving dataset for 3D object detection, we demonstrate the superiority of the doubly robust loss over the standard self-training baseline.

On Learning Necessary and Sufficient Causal Graphs

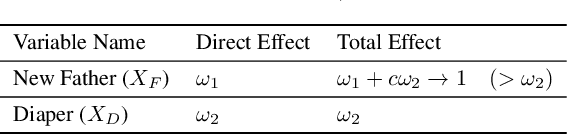
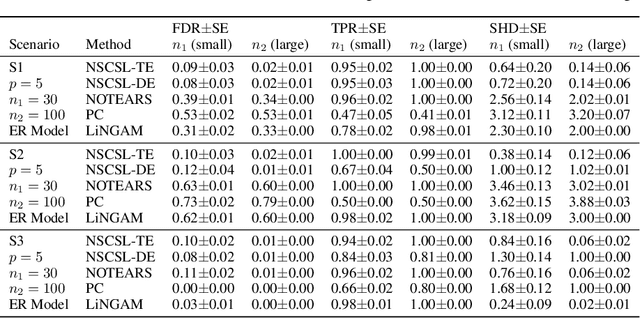
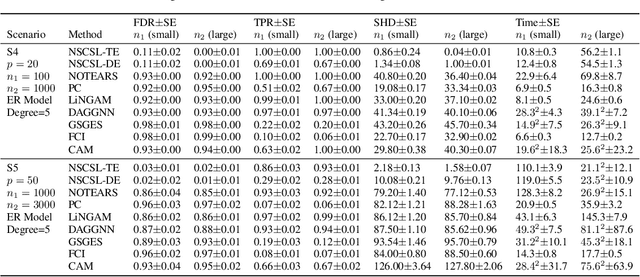
The causal revolution has spurred interest in understanding complex relationships in various fields. Most existing methods aim to discover causal relationships among all variables in a large-scale complex graph. However, in practice, only a small number of variables in the graph are relevant for the outcomes of interest. As a result, causal estimation with the full causal graph -- especially given limited data -- could lead to many falsely discovered, spurious variables that may be highly correlated with but have no causal impact on the target outcome. In this paper, we propose to learn a class of necessary and sufficient causal graphs (NSCG) that only contains causally relevant variables for an outcome of interest, which we term causal features. The key idea is to utilize probabilities of causation to systematically evaluate the importance of features in the causal graph, allowing us to identify a subgraph that is relevant to the outcome of interest. To learn NSCG from data, we develop a score-based necessary and sufficient causal structural learning (NSCSL) algorithm, by establishing theoretical relationships between probabilities of causation and causal effects of features. Across empirical studies of simulated and real data, we show that the proposed NSCSL algorithm outperforms existing algorithms and can reveal important yeast genes for target heritable traits of interest.

Neural Dependencies Emerging from Learning Massive Categories

This work presents two astonishing findings on neural networks learned for large-scale image classification. 1) Given a well-trained model, the logits predicted for some category can be directly obtained by linearly combining the predictions of a few other categories, which we call \textbf{neural dependency}. 2) Neural dependencies exist not only within a single model, but even between two independently learned models, regardless of their architectures. Towards a theoretical analysis of such phenomena, we demonstrate that identifying neural dependencies is equivalent to solving the Covariance Lasso (CovLasso) regression problem proposed in this paper. Through investigating the properties of the problem solution, we confirm that neural dependency is guaranteed by a redundant logit covariance matrix, which condition is easily met given massive categories, and that neural dependency is highly sparse, implying that one category correlates to only a few others. We further empirically show the potential of neural dependencies in understanding internal data correlations, generalizing models to unseen categories, and improving model robustness with a dependency-derived regularizer. Code for this work will be made publicly available.

Rank Diminishing in Deep Neural Networks

The rank of neural networks measures information flowing across layers. It is an instance of a key structural condition that applies across broad domains of machine learning. In particular, the assumption of low-rank feature representations leads to algorithmic developments in many architectures. For neural networks, however, the intrinsic mechanism that yields low-rank structures remains vague and unclear. To fill this gap, we perform a rigorous study on the behavior of network rank, focusing particularly on the notion of rank deficiency. We theoretically establish a universal monotonic decreasing property of network rank from the basic rules of differential and algebraic composition, and uncover rank deficiency of network blocks and deep function coupling. By virtue of our numerical tools, we provide the first empirical analysis of the per-layer behavior of network rank in practical settings, i.e., ResNets, deep MLPs, and Transformers on ImageNet. These empirical results are in direct accord with our theory. Furthermore, we reveal a novel phenomenon of independence deficit caused by the rank deficiency of deep networks, where classification confidence of a given category can be linearly decided by the confidence of a handful of other categories. The theoretical results of this work, together with the empirical findings, may advance understanding of the inherent principles of deep neural networks.