Panprediction: Optimal Predictions for Any Downstream Task and Loss

Supervised learning is classically formulated as training a model to minimize a fixed loss function over a fixed distribution, or task. However, an emerging paradigm instead views model training as extracting enough information from data so that the model can be used to minimize many losses on many downstream tasks. We formalize a mathematical framework for this paradigm, which we call panprediction, and study its statistical complexity. Formally, panprediction generalizes omniprediction and sits upstream from multi-group learning, which respectively focus on predictions that generalize to many downstream losses or many downstream tasks, but not both. Concretely, we design algorithms that learn deterministic and randomized panpredictors with $\tilde{O}(1/\varepsilon^3)$ and $\tilde{O}(1/\varepsilon^2)$ samples, respectively. Our results demonstrate that under mild assumptions, simultaneously minimizing infinitely many losses on infinitely many tasks can be as statistically easy as minimizing one loss on one task. Along the way, we improve the best known sample complexity guarantee of deterministic omniprediction by a factor of $1/\varepsilon$, and match all other known sample complexity guarantees of omniprediction and multi-group learning. Our key technical ingredient is a nearly lossless reduction from panprediction to a statistically efficient notion of calibration, called step calibration.

The Limits of Preference Data for Post-Training

Recent progress in strengthening the capabilities of large language models has stemmed from applying reinforcement learning to domains with automatically verifiable outcomes. A key question is whether we can similarly use RL to optimize for outcomes in domains where evaluating outcomes inherently requires human feedback; for example, in tasks like deep research and trip planning, outcome evaluation is qualitative and there are many possible degrees of success. One attractive and scalable modality for collecting human feedback is preference data: ordinal rankings (pairwise or $k$-wise) that indicate, for $k$ given outcomes, which one is preferred. In this work, we study a critical roadblock: preference data fundamentally and significantly limits outcome-based optimization. Even with idealized preference data (infinite, noiseless, and online), the use of ordinal feedback can prevent obtaining even approximately optimal solutions. We formalize this impossibility using voting theory, drawing an analogy between how a model chooses to answer a query with how voters choose a candidate to elect. This indicates that grounded human scoring and algorithmic innovations are necessary for extending the success of RL post-training to domains demanding human feedback. We also explore why these limitations have disproportionately impacted RLHF when it comes to eliciting reasoning behaviors (e.g., backtracking) versus situations where RLHF has been historically successful (e.g., instruction-tuning and safety training), finding that the limitations of preference data primarily suppress RLHF's ability to elicit robust strategies -- a class that encompasses most reasoning behaviors.

From Style to Facts: Mapping the Boundaries of Knowledge Injection with Finetuning

Finetuning provides a scalable and cost-effective means of customizing language models for specific tasks or response styles, with greater reliability than prompting or in-context learning. In contrast, the conventional wisdom is that injecting knowledge via finetuning results in brittle performance and poor generalization. We argue that the dichotomy of "task customization" (e.g., instruction tuning) and "knowledge injection" (e.g., teaching new facts) is a distinction without a difference. We instead identify concrete factors that explain the heterogeneous effectiveness observed with finetuning. To this end, we conduct a large-scale experimental study of finetuning the frontier Gemini v1.5 model family on a spectrum of datasets that are artificially engineered to interpolate between the strengths and failure modes of finetuning. Our findings indicate that question-answer training data formats provide much stronger knowledge generalization than document/article-style training data, numerical information can be harder for finetuning to retain than categorical information, and models struggle to apply finetuned knowledge during multi-step reasoning even when trained on similar examples -- all factors that render "knowledge injection" to be especially difficult, even after controlling for considerations like data augmentation and information volume. On the other hand, our findings also indicate that it is not fundamentally more difficult to finetune information about a real-world event than information about what a model's writing style should be.

Truthfulness of Decision-Theoretic Calibration Measures

Calibration measures quantify how much a forecaster's predictions violates calibration, which requires that forecasts are unbiased conditioning on the forecasted probabilities. Two important desiderata for a calibration measure are its decision-theoretic implications (i.e., downstream decision-makers that best-respond to the forecasts are always no-regret) and its truthfulness (i.e., a forecaster approximately minimizes error by always reporting the true probabilities). Existing measures satisfy at most one of the properties, but not both. We introduce a new calibration measure termed subsampled step calibration, $\mathsf{StepCE}^{\textsf{sub}}$, that is both decision-theoretic and truthful. In particular, on any product distribution, $\mathsf{StepCE}^{\textsf{sub}}$ is truthful up to an $O(1)$ factor whereas prior decision-theoretic calibration measures suffer from an $e^{-\Omega(T)}$-$\Omega(\sqrt{T})$ truthfulness gap. Moreover, in any smoothed setting where the conditional probability of each event is perturbed by a noise of magnitude $c > 0$, $\mathsf{StepCE}^{\textsf{sub}}$ is truthful up to an $O(\sqrt{\log(1/c)})$ factor, while prior decision-theoretic measures have an $e^{-\Omega(T)}$-$\Omega(T^{1/3})$ truthfulness gap. We also prove a general impossibility result for truthful decision-theoretic forecasting: any complete and decision-theoretic calibration measure must be discontinuous and non-truthful in the non-smoothed setting.

Sample, Scrutinize and Scale: Effective Inference-Time Search by Scaling Verification

Sampling-based search, a simple paradigm for utilizing test-time compute, involves generating multiple candidate responses and selecting the best one -- typically by verifying each response for correctness. In this paper, we study the scaling trends governing sampling-based search. Among our findings is that simply scaling up a minimalist implementation that uses only random sampling and direct self-verification results in sustained performance improvements that, for example, elevate the Gemini v1.5 Pro model's reasoning capabilities past that of o1-Preview on popular benchmarks. We partially attribute the scalability of sampling-based search to a phenomenon of implicit scaling, where sampling a larger pool of responses in turn improves verification accuracy. We further identify two useful principles for improving self-verification capabilities with test-time compute: (1) comparing across responses provides helpful signals about the locations of errors and hallucinations, and (2) different model output styles are useful for different contexts -- chains of thought are useful for reasoning but harder to verify. We also find that, though accurate verification can be elicited, frontier models demonstrate remarkably weak out-of-box verification capabilities and introduce a benchmark to measure progress on these deficiencies.

Relational Programming with Foundation Models

Foundation models have vast potential to enable diverse AI applications. The powerful yet incomplete nature of these models has spurred a wide range of mechanisms to augment them with capabilities such as in-context learning, information retrieval, and code interpreting. We propose Vieira, a declarative framework that unifies these mechanisms in a general solution for programming with foundation models. Vieira follows a probabilistic relational paradigm and treats foundation models as stateless functions with relational inputs and outputs. It supports neuro-symbolic applications by enabling the seamless combination of such models with logic programs, as well as complex, multi-modal applications by streamlining the composition of diverse sub-models. We implement Vieira by extending the Scallop compiler with a foreign interface that supports foundation models as plugins. We implement plugins for 12 foundation models including GPT, CLIP, and SAM. We evaluate Vieira on 9 challenging tasks that span language, vision, and structured and vector databases. Our evaluation shows that programs in Vieira are concise, can incorporate modern foundation models, and have comparable or better accuracy than competitive baselines.

Learning Variational Inequalities from Data: Fast Generalization Rates under Strong Monotonicity

Variational inequalities (VIs) are a broad class of optimization problems encompassing machine learning problems ranging from standard convex minimization to more complex scenarios like min-max optimization and computing the equilibria of multi-player games. In convex optimization, strong convexity allows for fast statistical learning rates requiring only $\Theta(1/\epsilon)$ stochastic first-order oracle calls to find an $\epsilon$-optimal solution, rather than the standard $\Theta(1/\epsilon^2)$ calls. In this paper, we explain how one can similarly obtain fast $\Theta(1/\epsilon)$ rates for learning VIs that satisfy strong monotonicity, a generalization of strong convexity. Specifically, we demonstrate that standard stability-based generalization arguments for convex minimization extend directly to VIs when the domain admits a small covering, or when the operator is integrable and suboptimality is measured by potential functions; such as when finding equilibria in multi-player games.

Learning With Multi-Group Guarantees For Clusterable Subpopulations

A canonical desideratum for prediction problems is that performance guarantees should hold not just on average over the population, but also for meaningful subpopulations within the overall population. But what constitutes a meaningful subpopulation? In this work, we take the perspective that relevant subpopulations should be defined with respect to the clusters that naturally emerge from the distribution of individuals for which predictions are being made. In this view, a population refers to a mixture model whose components constitute the relevant subpopulations. We suggest two formalisms for capturing per-subgroup guarantees: first, by attributing each individual to the component from which they were most likely drawn, given their features; and second, by attributing each individual to all components in proportion to their relative likelihood of having been drawn from each component. Using online calibration as a case study, we study a \variational algorithm that provides guarantees for each of these formalisms by handling all plausible underlying subpopulation structures simultaneously, and achieve an $O(T^{1/2})$ rate even when the subpopulations are not well-separated. In comparison, the more natural cluster-then-predict approach that first recovers the structure of the subpopulations and then makes predictions suffers from a $O(T^{2/3})$ rate and requires the subpopulations to be separable. Along the way, we prove that providing per-subgroup calibration guarantees for underlying clusters can be easier than learning the clusters: separation between median subgroup features is required for the latter but not the former.

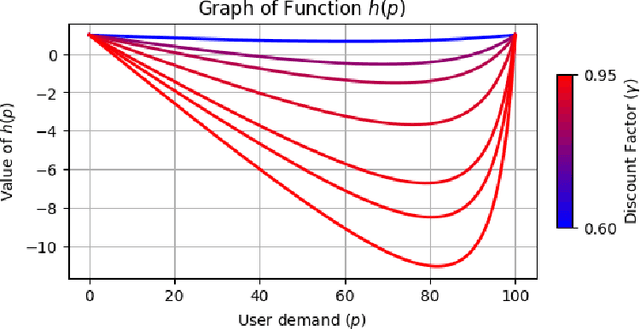
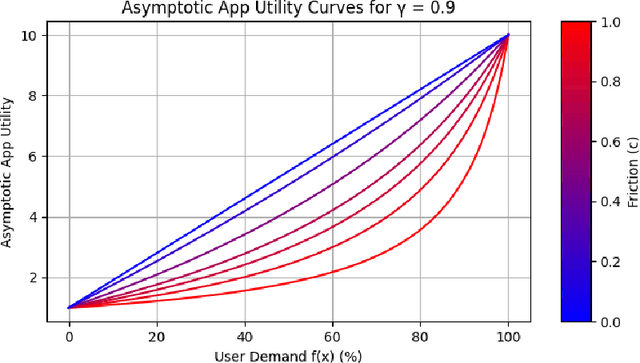
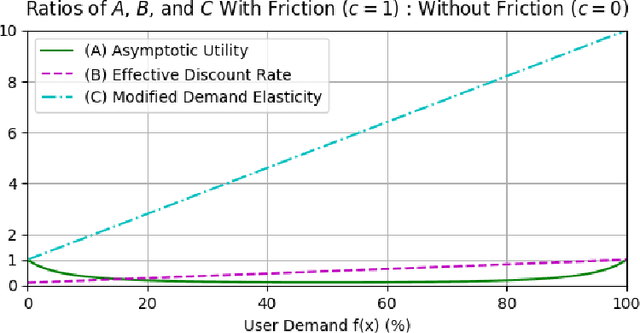
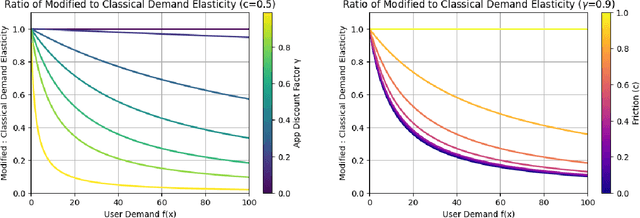
Algorithmic Content Selection and the Impact of User Disengagement

The content selection problem of digital services is often modeled as a decision-process where a service chooses, over multiple rounds, an arm to pull from a set of arms that each return a certain reward. This classical model does not account for the possibility that users disengage when dissatisfied and thus fails to capture an important trade-off between choosing content that promotes future engagement versus immediate reward. In this work, we introduce a model for the content selection problem where dissatisfied users may disengage and where the content that maximizes immediate reward does not necessarily maximize the odds of future user engagement. We show that when the relationship between each arm's expected reward and effect on user satisfaction are linearly related, an optimal content selection policy can be computed efficiently with dynamic programming under natural assumptions about the complexity of the users' engagement patterns. Moreover, we show that in an online learning setting where users with unknown engagement patterns arrive, there is a variant of Hedge that attains a $\tfrac 12$-competitive ratio regret bound. We also use our model to identify key primitives that determine how digital services should weigh engagement against revenue. For example, when it is more difficult for users to rejoin a service they are disengaged from, digital services naturally see a reduced payoff but user engagement may -- counterintuitively -- increase.

Truthfulness of Calibration Measures

We initiate the study of the truthfulness of calibration measures in sequential prediction. A calibration measure is said to be truthful if the forecaster (approximately) minimizes the expected penalty by predicting the conditional expectation of the next outcome, given the prior distribution of outcomes. Truthfulness is an important property of calibration measures, ensuring that the forecaster is not incentivized to exploit the system with deliberate poor forecasts. This makes it an essential desideratum for calibration measures, alongside typical requirements, such as soundness and completeness. We conduct a taxonomy of existing calibration measures and their truthfulness. Perhaps surprisingly, we find that all of them are far from being truthful. That is, under existing calibration measures, there are simple distributions on which a polylogarithmic (or even zero) penalty is achievable, while truthful prediction leads to a polynomial penalty. Our main contribution is the introduction of a new calibration measure termed the Subsampled Smooth Calibration Error (SSCE) under which truthful prediction is optimal up to a constant multiplicative factor.