Martin Jaggi
EPFL
Weight Decay may matter more than muP for Learning Rate Transfer in Practice
Oct 21, 2025Abstract:Transferring the optimal learning rate from small to large neural networks can enable efficient training at scales where hyperparameter tuning is otherwise prohibitively expensive. To this end, the Maximal Update Parameterization (muP) proposes a learning rate scaling designed to keep the update dynamics of internal representations stable across different model widths. However, the scaling rules of muP rely on strong assumptions, particularly about the geometric alignment of a layer's inputs with both its weights and gradient updates. In this large-scale empirical investigation, we show that these assumptions hold only briefly at the start of training in the practical setups where learning rate transfer is most valuable, such as LLM training. For the remainder of training it is weight decay rather than muP that correctly stabilizes the update dynamics of internal representations across widths, facilitating learning rate transfer. This suggests muP's scaling primarily acts as a form of implicit learning rate warmup, allowing us to largely replace it with modified warmup schedules. Together these findings fundamentally challenge prevailing beliefs about learning rate transfer and can explain empirical practice such as why muP requires the independent weight decay variant for successful transfer.
Apertus: Democratizing Open and Compliant LLMs for Global Language Environments
Sep 17, 2025
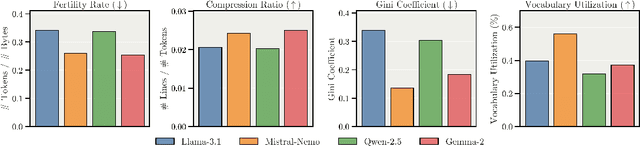

Abstract:We present Apertus, a fully open suite of large language models (LLMs) designed to address two systemic shortcomings in today's open model ecosystem: data compliance and multilingual representation. Unlike many prior models that release weights without reproducible data pipelines or regard for content-owner rights, Apertus models are pretrained exclusively on openly available data, retroactively respecting robots.txt exclusions and filtering for non-permissive, toxic, and personally identifiable content. To mitigate risks of memorization, we adopt the Goldfish objective during pretraining, strongly suppressing verbatim recall of data while retaining downstream task performance. The Apertus models also expand multilingual coverage, training on 15T tokens from over 1800 languages, with ~40% of pretraining data allocated to non-English content. Released at 8B and 70B scales, Apertus approaches state-of-the-art results among fully open models on multilingual benchmarks, rivalling or surpassing open-weight counterparts. Beyond model weights, we release all scientific artifacts from our development cycle with a permissive license, including data preparation scripts, checkpoints, evaluation suites, and training code, enabling transparent audit and extension.
TiMoE: Time-Aware Mixture of Language Experts
Aug 12, 2025



Abstract:Large language models (LLMs) are typically trained on fixed snapshots of the web, which means that their knowledge becomes stale and their predictions risk temporal leakage: relying on information that lies in the future relative to a query. We tackle this problem by pre-training from scratch a set of GPT-style experts on disjoint two-year slices of a 2013-2024 corpus and combining them through TiMoE, a Time-aware Mixture of Language Experts. At inference time, TiMoE masks all experts whose training window ends after the query timestamp and merges the remaining log-probabilities in a shared space, guaranteeing strict causal validity while retaining the breadth of multi-period knowledge. We also release TSQA, a 10k-question benchmark whose alternatives are explicitly labelled as past, future or irrelevant, allowing fine-grained measurement of temporal hallucinations. Experiments on eight standard NLP tasks plus TSQA show that a co-adapted TiMoE variant matches or exceeds the best single-period expert and cuts future-knowledge errors by up to 15%. Our results demonstrate that modular, time-segmented pre-training paired with causal routing is a simple yet effective path toward LLMs that stay chronologically grounded without sacrificing general performance much. We open source our code at TiMoE (Github): https://github.com/epfml/TiMoE
FineWeb2: One Pipeline to Scale Them All -- Adapting Pre-Training Data Processing to Every Language
Jun 26, 2025Abstract:Pre-training state-of-the-art large language models (LLMs) requires vast amounts of clean and diverse text data. While the open development of large high-quality English pre-training datasets has seen substantial recent progress, training performant multilingual LLMs remains a challenge, in large part due to the inherent difficulty of tailoring filtering and deduplication pipelines to a large number of languages. In this work, we introduce a new pre-training dataset curation pipeline based on FineWeb that can be automatically adapted to support any language. We extensively ablate our pipeline design choices on a set of nine diverse languages, guided by a set of meaningful and informative evaluation tasks that were chosen through a novel selection process based on measurable criteria. Ultimately, we show that our pipeline can be used to create non-English corpora that produce more performant models than prior datasets. We additionally introduce a straightforward and principled approach to rebalance datasets that takes into consideration both duplication count and quality, providing an additional performance uplift. Finally, we scale our pipeline to over 1000 languages using almost 100 Common Crawl snapshots to produce FineWeb2, a new 20 terabyte (5 billion document) multilingual dataset which we release along with our pipeline, training, and evaluation codebases.
Gradient-Normalized Smoothness for Optimization with Approximate Hessians
Jun 16, 2025



Abstract:In this work, we develop new optimization algorithms that use approximate second-order information combined with the gradient regularization technique to achieve fast global convergence rates for both convex and non-convex objectives. The key innovation of our analysis is a novel notion called Gradient-Normalized Smoothness, which characterizes the maximum radius of a ball around the current point that yields a good relative approximation of the gradient field. Our theory establishes a natural intrinsic connection between Hessian approximation and the linearization of the gradient. Importantly, Gradient-Normalized Smoothness does not depend on the specific problem class of the objective functions, while effectively translating local information about the gradient field and Hessian approximation into the global behavior of the method. This new concept equips approximate second-order algorithms with universal global convergence guarantees, recovering state-of-the-art rates for functions with H\"older-continuous Hessians and third derivatives, quasi-self-concordant functions, as well as smooth classes in first-order optimization. These rates are achieved automatically and extend to broader classes, such as generalized self-concordant functions. We demonstrate direct applications of our results for global linear rates in logistic regression and softmax problems with approximate Hessians, as well as in non-convex optimization using Fisher and Gauss-Newton approximations.
Towards Fully FP8 GEMM LLM Training at Scale
May 26, 2025Abstract:Despite the significant potential of FP8 data formats for large language model (LLM) pre-training, their adoption has been limited due to challenges in maintaining stability at scale. Existing approaches often rely on suboptimal fine-grained FP8 kernels or fall back to higher-precision matrix multiplications (GEMMs) in sensitive components, such as attention projections, compromising potential throughput gains. We introduce a new class of LLM architectures that, for the first time, support FP8 computation for all GEMMs within transformer blocks during both forward and backward passes. This enables unprecedented throughput gains, particularly at scale, while matching the downstream performance of standard BF16 training. Our architecture design reduces large outlier activations, promoting stable long-term FP8 training. In addition, we identify key metrics to monitor low-precision training and predict potential future divergences.
GRAPE: Optimize Data Mixture for Group Robust Multi-target Adaptive Pretraining
May 26, 2025



Abstract:The performance of large language models (LLMs) across diverse downstream applications is fundamentally governed by the quality and composition of their pretraining corpora. Existing domain reweighting algorithms primarily optimize data mixtures for a single target task, thereby resulting in models that overfit to specialized objectives while exhibiting substantial performance degradation on other benchmarks. This paper introduces Group Robust Multi-target Adaptive PrEtraining (GRAPE), a novel multi-source-multi-target domain reweighting framework designed to calibrate pretraining data mixtures for robust performance across multiple target tasks simultaneously. GRAPE dynamically adjusts sampling weights across source domains (domain weights) while concurrently modulating task weights that quantify the relative importance of each individual target task. This adaptive process prioritizes tasks based on their learning difficulty throughout training. We formulate this interleaved reweighting mechanism as a minimax optimization problem: The inner maximization adjusts task weights leveraging group distributed-robust-optimization (DRO), where those tasks demonstrating the least improvement under the current data mixture are prioritized with higher weights; The outer minimization then optimizes domain weights to maximize loss reduction on the prioritized tasks. Experiments on ClimbLab and SlimPajama datasets demonstrate that GRAPE consistently outperforms baseline methods in terms of reasoning performance across 6 benchmarks. Furthermore, when applied to multilingual targets, GRAPE effectively identifies optimal training mixtures from mainstream languages, achieving superior language modeling capabilities across 8 low-resource target languages.
URLs Help, Topics Guide: Understanding Metadata Utility in LLM Training
May 22, 2025Abstract:Large Language Models (LLMs) are commonly pretrained on vast corpora of text without utilizing contextual metadata such as source, quality, or topic, leading to a context-free learning paradigm. While recent studies suggest that adding metadata like URL information as context (i.e., auxiliary inputs not used in the loss calculation) can improve training efficiency and downstream performance, they offer limited understanding of which types of metadata are truly effective and under what conditions. In this work, we conduct a systematic evaluation and find that not all metadata types contribute equally. Only URL context speeds up training, whereas quality scores and topic/format domain information offer no clear benefit. Furthermore, the improved downstream performances of URL conditioning emerge only when longer prompts are used at inference time. In addition, we demonstrate that context-aware pretraining enables more controllable generation than context-free pretraining, in a classifier-free guidance fashion. Although topic and format metadata do not accelerate training, they are effective for steering outputs, offering human-interpretable control over generation.
NeuralGrok: Accelerate Grokking by Neural Gradient Transformation
Apr 24, 2025Abstract:Grokking is proposed and widely studied as an intricate phenomenon in which generalization is achieved after a long-lasting period of overfitting. In this work, we propose NeuralGrok, a novel gradient-based approach that learns an optimal gradient transformation to accelerate the generalization of transformers in arithmetic tasks. Specifically, NeuralGrok trains an auxiliary module (e.g., an MLP block) in conjunction with the base model. This module dynamically modulates the influence of individual gradient components based on their contribution to generalization, guided by a bilevel optimization algorithm. Our extensive experiments demonstrate that NeuralGrok significantly accelerates generalization, particularly in challenging arithmetic tasks. We also show that NeuralGrok promotes a more stable training paradigm, constantly reducing the model's complexity, while traditional regularization methods, such as weight decay, can introduce substantial instability and impede generalization. We further investigate the intrinsic model complexity leveraging a novel Absolute Gradient Entropy (AGE) metric, which explains that NeuralGrok effectively facilitates generalization by reducing the model complexity. We offer valuable insights on the grokking phenomenon of Transformer models, which encourages a deeper understanding of the fundamental principles governing generalization ability.
Can Performant LLMs Be Ethical? Quantifying the Impact of Web Crawling Opt-Outs
Apr 08, 2025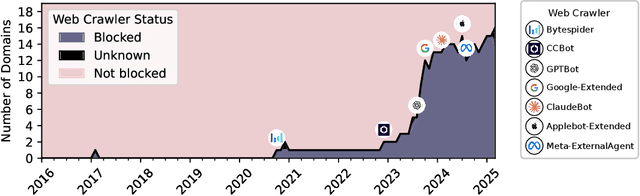



Abstract:The increasing adoption of web crawling opt-outs by copyright holders of online content raises critical questions about the impact of data compliance on large language model (LLM) performance. However, little is known about how these restrictions (and the resultant filtering of pretraining datasets) affect the capabilities of models trained using these corpora. In this work, we conceptualize this effect as the $\textit{data compliance gap}$ (DCG), which quantifies the performance difference between models trained on datasets that comply with web crawling opt-outs, and those that do not. We measure the data compliance gap in two settings: pretraining models from scratch and continual pretraining from existing compliant models (simulating a setting where copyrighted data could be integrated later in pretraining). Our experiments with 1.5B models show that, as of January 2025, compliance with web data opt-outs does not degrade general knowledge acquisition (close to 0\% DCG). However, in specialized domains such as biomedical research, excluding major publishers leads to performance declines. These findings suggest that while general-purpose LLMs can be trained to perform equally well using fully open data, performance in specialized domains may benefit from access to high-quality copyrighted sources later in training. Our study provides empirical insights into the long-debated trade-off between data compliance and downstream model performance, informing future discussions on AI training practices and policy decisions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge