Laminating Representation Autoencoders for Efficient Diffusion

Recent work has shown that diffusion models can generate high-quality images by operating directly on SSL patch features rather than pixel-space latents. However, the dense patch grids from encoders like DINOv2 contain significant redundancy, making diffusion needlessly expensive. We introduce FlatDINO, a variational autoencoder that compresses this representation into a one-dimensional sequence of just 32 continuous tokens -an 8x reduction in sequence length and 48x compression in total dimensionality. On ImageNet 256x256, a DiT-XL trained on FlatDINO latents achieves a gFID of 1.80 with classifier-free guidance while requiring 8x fewer FLOPs per forward pass and up to 4.5x fewer FLOPs per training step compared to diffusion on uncompressed DINOv2 features. These are preliminary results and this work is in progress.

Thinking Slow, Fast: Scaling Inference Compute with Distilled Reasoners

Recent advancements have demonstrated that the performance of large language models (LLMs) can be significantly enhanced by scaling computational resources at test time. A common strategy involves generating multiple Chain-of-Thought (CoT) trajectories and aggregating their outputs through various selection mechanisms. This raises a fundamental question: can models with lower complexity leverage their superior generation throughput to outperform similarly sized Transformers for a fixed computational budget? To address this question and overcome the lack of strong subquadratic reasoners, we distill pure and hybrid Mamba models from pretrained Transformers. Trained on only 8 billion tokens, our distilled models show strong performance and scaling on mathematical reasoning datasets while being much faster at inference for large batches and long sequences. Despite the zero-shot performance hit due to distillation, both pure and hybrid Mamba models can scale their coverage and accuracy performance past their Transformer teacher models under fixed time budgets, opening a new direction for scaling inference compute.

Leveraging the true depth of LLMs

Large Language Models demonstrate remarkable capabilities at the cost of high compute requirements. While recent research has shown that intermediate layers can be removed or have their order shuffled without impacting performance significantly, these findings have not been employed to reduce the computational cost of inference. We investigate several potential ways to reduce the depth of pre-trained LLMs without significantly affecting performance. Leveraging our insights, we present a novel approach that exploits this decoupling between layers by grouping some of them into pairs that can be evaluated in parallel. This modification of the computational graph -- through better parallelism -- results in an average improvement of around 1.20x on the number of tokens generated per second, without re-training nor fine-tuning, while retaining 95%-99% of the original accuracy. Empirical evaluation demonstrates that this approach significantly improves serving efficiency while maintaining model performance, offering a practical improvement for large-scale LLM deployment.

Solvation Free Energies from Neural Thermodynamic Integration

We propose to compute solvation free energies via thermodynamic integration along a neural-network potential interpolating between two target Hamiltonians. We use a stochastic interpolant to define an interpolation between the distributions at the level of samples and optimize a neural network potential to match the corresponding equilibrium potential at every intermediate time-step. Once the alignment between the interpolating samples and the interpolating potentials is sufficiently accurate, the free-energy difference between the two Hamiltonians can be estimated using (neural) thermodynamic integration. We validate our method to compute solvation free energies on several benchmark systems: a Lennard-Jones particle in a Lennard-Jones fluid, as well as the insertion of both water and methane solutes in a water solvent at atomistic resolution.

Efficient World Models with Context-Aware Tokenization

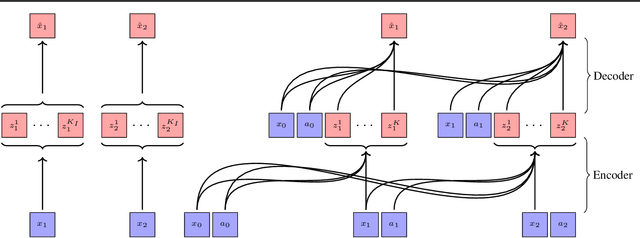
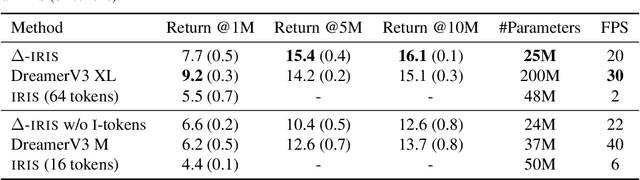
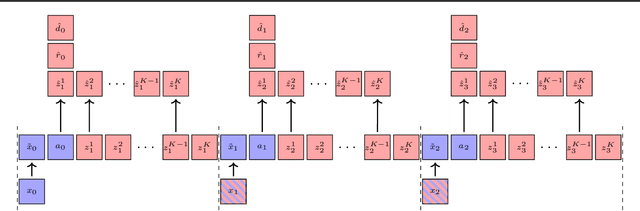
Scaling up deep Reinforcement Learning (RL) methods presents a significant challenge. Following developments in generative modelling, model-based RL positions itself as a strong contender. Recent advances in sequence modelling have led to effective transformer-based world models, albeit at the price of heavy computations due to the long sequences of tokens required to accurately simulate environments. In this work, we propose $\Delta$-IRIS, a new agent with a world model architecture composed of a discrete autoencoder that encodes stochastic deltas between time steps and an autoregressive transformer that predicts future deltas by summarizing the current state of the world with continuous tokens. In the Crafter benchmark, $\Delta$-IRIS sets a new state of the art at multiple frame budgets, while being an order of magnitude faster to train than previous attention-based approaches. We release our code and models at https://github.com/vmicheli/delta-iris.

Neural Thermodynamic Integration: Free Energies from Energy-based Diffusion Models

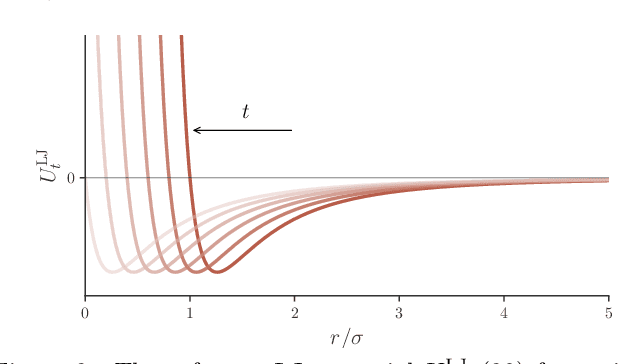
Thermodynamic integration (TI) offers a rigorous method for estimating free-energy differences by integrating over a sequence of interpolating conformational ensembles. However, TI calculations are computationally expensive and typically limited to coupling a small number of degrees of freedom due to the need to sample numerous intermediate ensembles with sufficient conformational-space overlap. In this work, we propose to perform TI along an alchemical pathway represented by a trainable neural network, which we term Neural TI. Critically, we parametrize a time-dependent Hamiltonian interpolating between the interacting and non-interacting systems, and optimize its gradient using a denoising-diffusion objective. The ability of the resulting energy-based diffusion model to sample all intermediate ensembles, allows us to perform TI from a single reference calculation. We apply our method to Lennard-Jones fluids, where we report accurate calculations of the excess chemical potential, demonstrating that Neural TI is capable of coupling hundreds of degrees of freedom at once.

Diffusion for World Modeling: Visual Details Matter in Atari

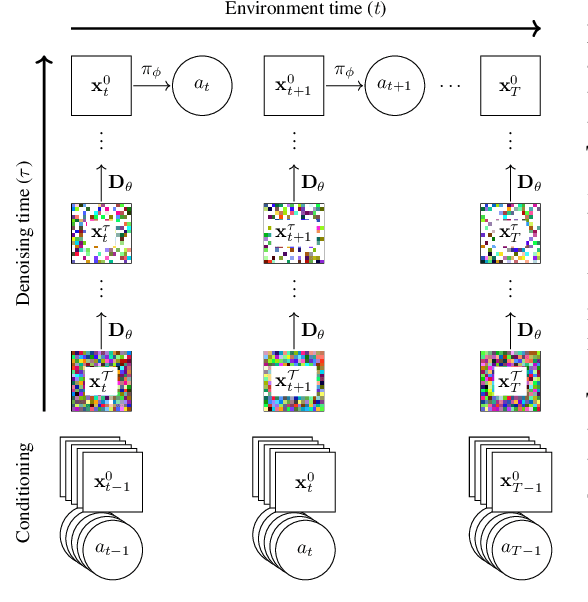
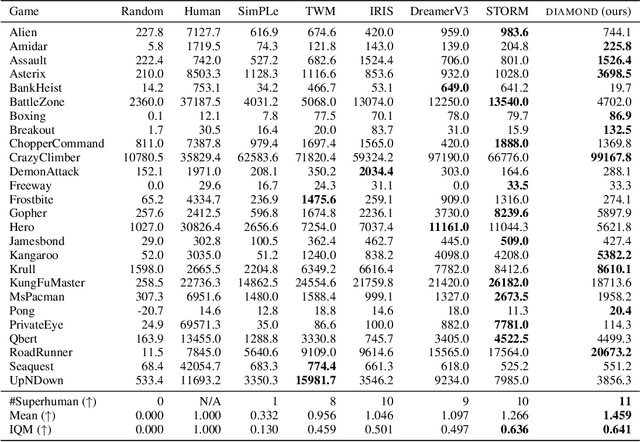
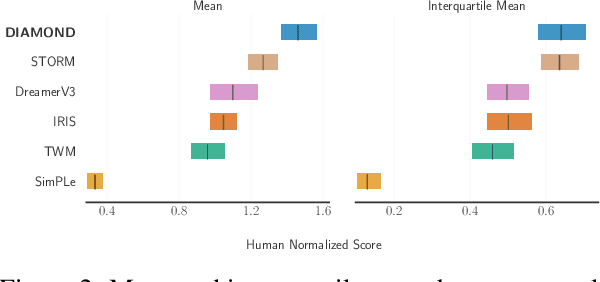
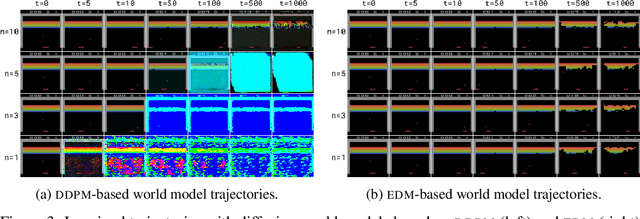
World models constitute a promising approach for training reinforcement learning agents in a safe and sample-efficient manner. Recent world models predominantly operate on sequences of discrete latent variables to model environment dynamics. However, this compression into a compact discrete representation may ignore visual details that are important for reinforcement learning. Concurrently, diffusion models have become a dominant approach for image generation, challenging well-established methods modeling discrete latents. Motivated by this paradigm shift, we introduce DIAMOND (DIffusion As a Model Of eNvironment Dreams), a reinforcement learning agent trained in a diffusion world model. We analyze the key design choices that are required to make diffusion suitable for world modeling, and demonstrate how improved visual details can lead to improved agent performance. DIAMOND achieves a mean human normalized score of 1.46 on the competitive Atari 100k benchmark; a new best for agents trained entirely within a world model. To foster future research on diffusion for world modeling, we release our code, agents and playable world models at https://github.com/eloialonso/diamond.

Localizing Task Information for Improved Model Merging and Compression

Model merging and task arithmetic have emerged as promising scalable approaches to merge multiple single-task checkpoints to one multi-task model, but their applicability is reduced by significant performance loss. Previous works have linked these drops to interference in the weight space and erasure of important task-specific features. Instead, in this work we show that the information required to solve each task is still preserved after merging as different tasks mostly use non-overlapping sets of weights. We propose TALL-masks, a method to identify these task supports given a collection of task vectors and show that one can retrieve >99% of the single task accuracy by applying our masks to the multi-task vector, effectively compressing the individual checkpoints. We study the statistics of intersections among constructed masks and reveal the existence of selfish and catastrophic weights, i.e., parameters that are important exclusively to one task and irrelevant to all tasks but detrimental to multi-task fusion. For this reason, we propose Consensus Merging, an algorithm that eliminates such weights and improves the general performance of existing model merging approaches. Our experiments in vision and NLP benchmarks with up to 20 tasks, show that Consensus Merging consistently improves existing approaches. Furthermore, our proposed compression scheme reduces storage from 57Gb to 8.2Gb while retaining 99.7% of original performance.

σ-GPTs: A New Approach to Autoregressive Models

Autoregressive models, such as the GPT family, use a fixed order, usually left-to-right, to generate sequences. However, this is not a necessity. In this paper, we challenge this assumption and show that by simply adding a positional encoding for the output, this order can be modulated on-the-fly per-sample which offers key advantageous properties. It allows for the sampling of and conditioning on arbitrary subsets of tokens, and it also allows sampling in one shot multiple tokens dynamically according to a rejection strategy, leading to a sub-linear number of model evaluations. We evaluate our method across various domains, including language modeling, path-solving, and aircraft vertical rate prediction, decreasing the number of steps required for generation by an order of magnitude.

Multi-Lattice Sampling of Quantum Field Theories via Neural Operator-based Flows

We consider the problem of sampling discrete field configurations $\phi$ from the Boltzmann distribution $[d\phi] Z^{-1} e^{-S[\phi]}$, where $S$ is the lattice-discretization of the continuous Euclidean action $\mathcal S$ of some quantum field theory. Since such densities arise as the approximation of the underlying functional density $[\mathcal D\phi(x)] \mathcal Z^{-1} e^{-\mathcal S[\phi(x)]}$, we frame the task as an instance of operator learning. In particular, we propose to approximate a time-dependent operator $\mathcal V_t$ whose time integral provides a mapping between the functional distributions of the free theory $[\mathcal D\phi(x)] \mathcal Z_0^{-1} e^{-\mathcal S_{0}[\phi(x)]}$ and of the target theory $[\mathcal D\phi(x)]\mathcal Z^{-1}e^{-\mathcal S[\phi(x)]}$. Whenever a particular lattice is chosen, the operator $\mathcal V_t$ can be discretized to a finite dimensional, time-dependent vector field $V_t$ which in turn induces a continuous normalizing flow between finite dimensional distributions over the chosen lattice. This flow can then be trained to be a diffeormorphism between the discretized free and target theories $[d\phi] Z_0^{-1} e^{-S_{0}[\phi]}$, $[d\phi] Z^{-1}e^{-S[\phi]}$. We run experiments on the $\phi^4$-theory to explore to what extent such operator-based flow architectures generalize to lattice sizes they were not trained on and show that pretraining on smaller lattices can lead to speedup over training only a target lattice size.