Solvation Free Energies from Neural Thermodynamic Integration

We propose to compute solvation free energies via thermodynamic integration along a neural-network potential interpolating between two target Hamiltonians. We use a stochastic interpolant to define an interpolation between the distributions at the level of samples and optimize a neural network potential to match the corresponding equilibrium potential at every intermediate time-step. Once the alignment between the interpolating samples and the interpolating potentials is sufficiently accurate, the free-energy difference between the two Hamiltonians can be estimated using (neural) thermodynamic integration. We validate our method to compute solvation free energies on several benchmark systems: a Lennard-Jones particle in a Lennard-Jones fluid, as well as the insertion of both water and methane solutes in a water solvent at atomistic resolution.

Neural Thermodynamic Integration: Free Energies from Energy-based Diffusion Models

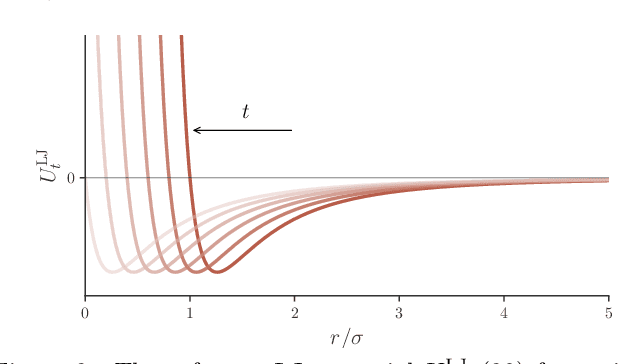
Thermodynamic integration (TI) offers a rigorous method for estimating free-energy differences by integrating over a sequence of interpolating conformational ensembles. However, TI calculations are computationally expensive and typically limited to coupling a small number of degrees of freedom due to the need to sample numerous intermediate ensembles with sufficient conformational-space overlap. In this work, we propose to perform TI along an alchemical pathway represented by a trainable neural network, which we term Neural TI. Critically, we parametrize a time-dependent Hamiltonian interpolating between the interacting and non-interacting systems, and optimize its gradient using a denoising-diffusion objective. The ability of the resulting energy-based diffusion model to sample all intermediate ensembles, allows us to perform TI from a single reference calculation. We apply our method to Lennard-Jones fluids, where we report accurate calculations of the excess chemical potential, demonstrating that Neural TI is capable of coupling hundreds of degrees of freedom at once.

Multi-Lattice Sampling of Quantum Field Theories via Neural Operator-based Flows

We consider the problem of sampling discrete field configurations $\phi$ from the Boltzmann distribution $[d\phi] Z^{-1} e^{-S[\phi]}$, where $S$ is the lattice-discretization of the continuous Euclidean action $\mathcal S$ of some quantum field theory. Since such densities arise as the approximation of the underlying functional density $[\mathcal D\phi(x)] \mathcal Z^{-1} e^{-\mathcal S[\phi(x)]}$, we frame the task as an instance of operator learning. In particular, we propose to approximate a time-dependent operator $\mathcal V_t$ whose time integral provides a mapping between the functional distributions of the free theory $[\mathcal D\phi(x)] \mathcal Z_0^{-1} e^{-\mathcal S_{0}[\phi(x)]}$ and of the target theory $[\mathcal D\phi(x)]\mathcal Z^{-1}e^{-\mathcal S[\phi(x)]}$. Whenever a particular lattice is chosen, the operator $\mathcal V_t$ can be discretized to a finite dimensional, time-dependent vector field $V_t$ which in turn induces a continuous normalizing flow between finite dimensional distributions over the chosen lattice. This flow can then be trained to be a diffeormorphism between the discretized free and target theories $[d\phi] Z_0^{-1} e^{-S_{0}[\phi]}$, $[d\phi] Z^{-1}e^{-S[\phi]}$. We run experiments on the $\phi^4$-theory to explore to what extent such operator-based flow architectures generalize to lattice sizes they were not trained on and show that pretraining on smaller lattices can lead to speedup over training only a target lattice size.

Graph Neural Networks Go Forward-Forward

We present the Graph Forward-Forward (GFF) algorithm, an extension of the Forward-Forward procedure to graphs, able to handle features distributed over a graph's nodes. This allows training graph neural networks with forward passes only, without backpropagation. Our method is agnostic to the message-passing scheme, and provides a more biologically plausible learning scheme than backpropagation, while also carrying computational advantages. With GFF, graph neural networks are trained greedily layer by layer, using both positive and negative samples. We run experiments on 11 standard graph property prediction tasks, showing how GFF provides an effective alternative to backpropagation for training graph neural networks. This shows in particular that this procedure is remarkably efficient in spite of combining the per-layer training with the locality of the processing in a GNN.

Learning Deformation Trajectories of Boltzmann Densities

We introduce a training objective for continuous normalizing flows that can be used in the absence of samples but in the presence of an energy function. Our method relies on either a prescribed or a learnt interpolation $f_t$ of energy functions between the target energy $f_1$ and the energy function of a generalized Gaussian $f_0(x) = (|x|/\sigma)^p$. This then induces an interpolation of Boltzmann densities $p_t \propto e^{-f_t}$ and we aim to find a time-dependent vector field $V_t$ that transports samples along this family of densities. Concretely, this condition can be translated to a PDE between $V_t$ and $f_t$ and we minimize the amount by which this PDE fails to hold. We compare this objective to the reverse KL-divergence on Gaussian mixtures and on the $\phi^4$ lattice field theory on a circle.

Deformation Theory of Boltzmann Distributions

Consider a one-parameter family of Boltzmann distributions $p_t(x) = \tfrac{1}{Z_t}e^{-S_t(x)}$. We study the problem of sampling from $p_{t_0}$ by first sampling from $p_{t_1}$ and then applying a transformation $\Psi_{t_1}^{t_0}$ to the samples so that to they follow $p_{t_0}$. We derive an equation relating $\Psi$ and the corresponding family of unnormalized log-likelihoods $S_t$. We demonstrate the utility of this idea on the $\phi^4$ lattice field theory by extending its defining action $S_0$ to a family of actions $S_t$ and finding a $\tau$ such that normalizing flows perform better at learning the Boltzmann distribution $p_\tau$ than at learning $p_0$.

Flowification: Everything is a Normalizing Flow

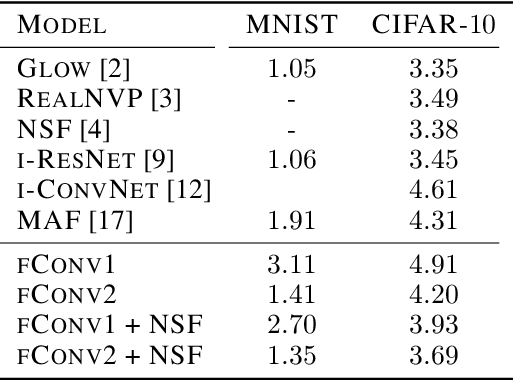
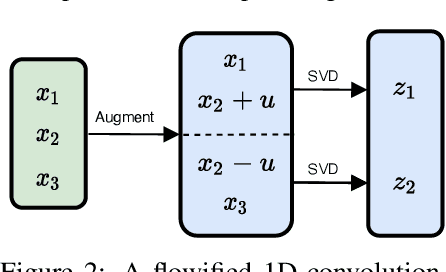
We develop a method that can be used to turn any multi-layer perceptron or convolutional network into a normalizing flow. In some cases this requires the addition of uncorrelated noise to the model but in the simplest case no additional parameters. The technique we develop can be applied to a broad range of architectures, allowing them to be used for a wide range of tasks. Our models also allow existing density estimation techniques to be combined with high performance feature extractors. In contrast to standard density estimation techniques that require specific architectures and specialized knowledge, our approach can leverage design knowledge from other domains and is a step closer to the realization of general purpose architectures. We investigate the efficacy of linear and convolutional layers for the task of density estimation on standard datasets. Our results suggest standard layers lack something fundamental in comparison to other normalizing flows.

Beyond Ansätze: Learning Quantum Circuits as Unitary Operators

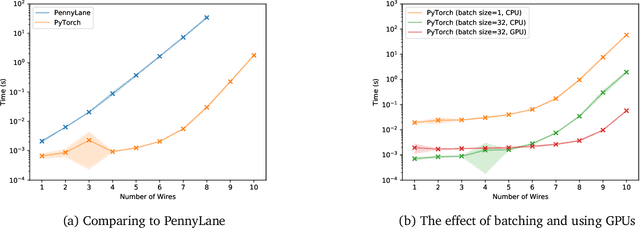
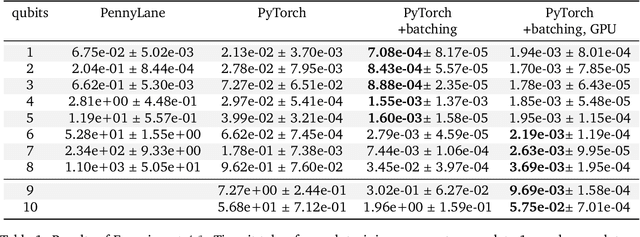
This paper explores the advantages of optimizing quantum circuits on $N$ wires as operators in the unitary group $U(2^N)$. We run gradient-based optimization in the Lie algebra $\mathfrak u(2^N)$ and use the exponential map to parametrize unitary matrices. We argue that $U(2^N)$ is not only more general than the search space induced by an ansatz, but in ways easier to work with on classical computers. The resulting approach is quick, ansatz-free and provides an upper bound on performance over all ans\"atze on $N$ wires.

SUPA: A Lightweight Diagnostic Simulator for Machine Learning in Particle Physics

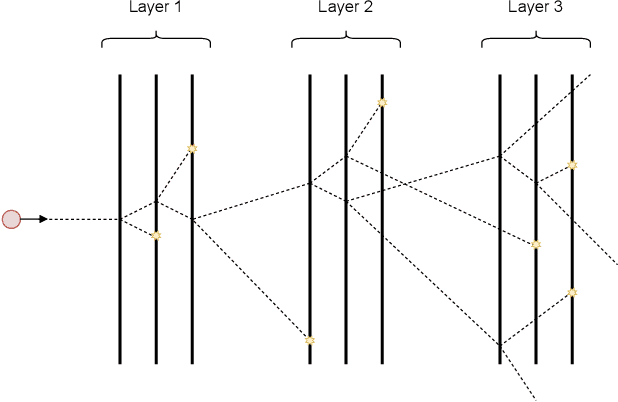
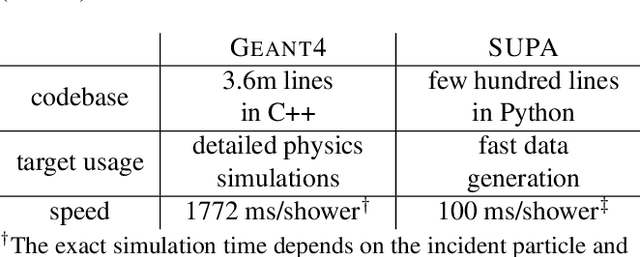
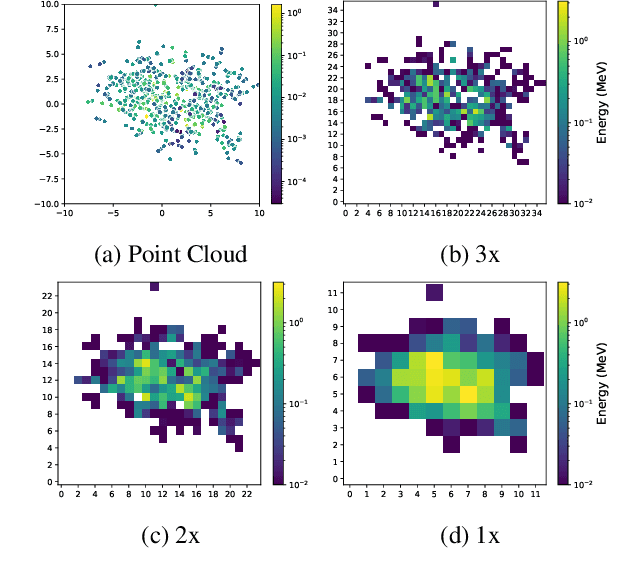
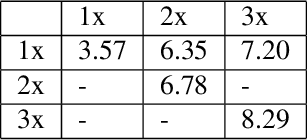
Deep learning methods have gained popularity in high energy physics for fast modeling of particle showers in detectors. Detailed simulation frameworks such as the gold standard Geant4 are computationally intensive, and current deep generative architectures work on discretized, lower resolution versions of the detailed simulation. The development of models that work at higher spatial resolutions is currently hindered by the complexity of the full simulation data, and by the lack of simpler, more interpretable benchmarks. Our contribution is SUPA, the SUrrogate PArticle propagation simulator, an algorithm and software package for generating data by simulating simplified particle propagation, scattering and shower development in matter. The generation is extremely fast and easy to use compared to Geant4, but still exhibits the key characteristics and challenges of the detailed simulation. We support this claim experimentally by showing that performance of generative models on data from our simulator reflects the performance on a dataset generated with Geant4. The proposed simulator generates thousands of particle showers per second on a desktop machine, a speed up of up to 6 orders of magnitudes over Geant4, and stores detailed geometric information about the shower propagation. SUPA provides much greater flexibility for setting initial conditions and defining multiple benchmarks for the development of models. Moreover, interpreting particle showers as point clouds creates a connection to geometric machine learning and provides challenging and fundamentally new datasets for the field. The code for SUPA is available at https://github.com/itsdaniele/SUPA.

Priming PCA with EigenGame

We introduce primed-PCA (pPCA), an extension of the recently proposed EigenGame algorithm for computing principal components in a large-scale setup. Our algorithm first runs EigenGame to get an approximation of the principal components, and then applies an exact PCA in the subspace they span. Since this subspace is of small dimension in any practical use of EigenGame, this second step is extremely cheap computationally. Nonetheless, it improves accuracy significantly for a given computational budget across datasets. In this setup, the purpose of EigenGame is to narrow down the search space, and prepare the data for the second step, an exact calculation. We show formally that pPCA improves upon EigenGame under very mild conditions, and we provide experimental validation on both synthetic and real large-scale datasets showing that it systematically translates to improved performance. In our experiments we achieve improvements in convergence speed by factors of 5-25 on the datasets of the original EigenGame paper.