Strategic White Paper on AI Infrastructure for Particle, Nuclear, and Astroparticle Physics: Insights from JENA and EuCAIF

Artificial intelligence (AI) is transforming scientific research, with deep learning methods playing a central role in data analysis, simulations, and signal detection across particle, nuclear, and astroparticle physics. Within the JENA communities-ECFA, NuPECC, and APPEC-and as part of the EuCAIF initiative, AI integration is advancing steadily. However, broader adoption remains constrained by challenges such as limited computational resources, a lack of expertise, and difficulties in transitioning from research and development (R&D) to production. This white paper provides a strategic roadmap, informed by a community survey, to address these barriers. It outlines critical infrastructure requirements, prioritizes training initiatives, and proposes funding strategies to scale AI capabilities across fundamental physics over the next five years.

End-to-End Optimal Detector Design with Mutual Information Surrogates

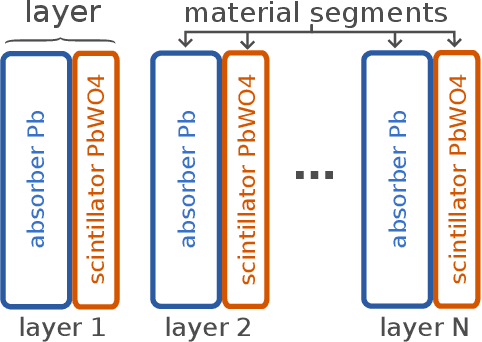
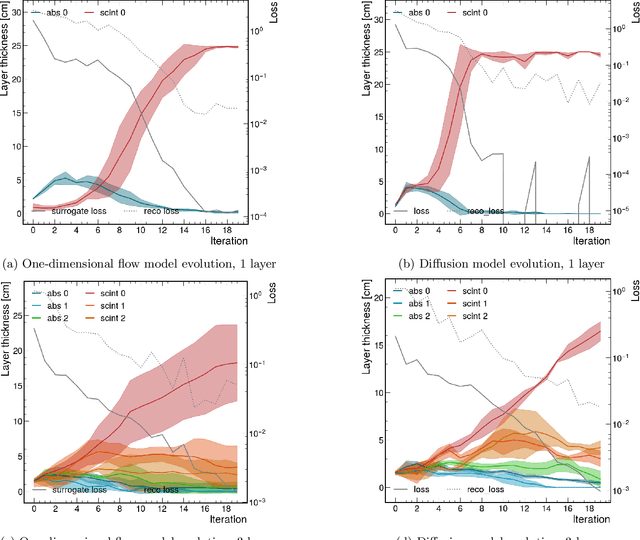
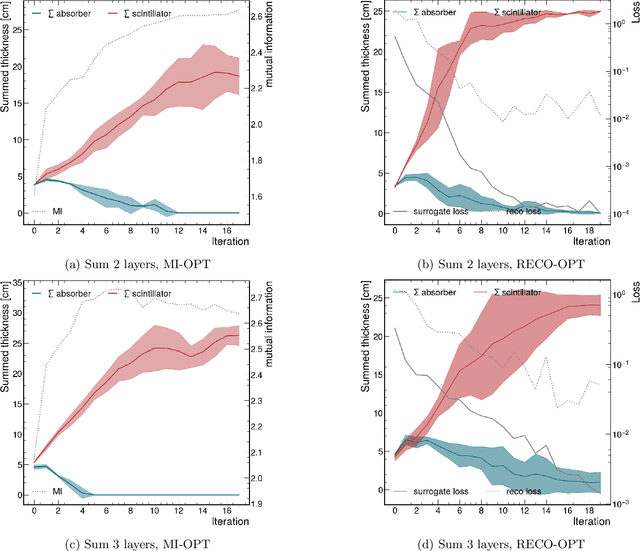
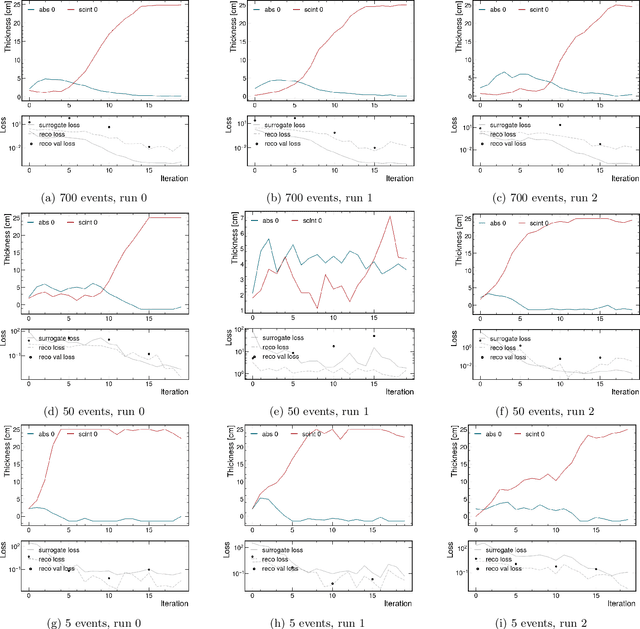
We introduce a novel approach for end-to-end black-box optimization of high energy physics (HEP) detectors using local deep learning (DL) surrogates. These surrogates approximate a scalar objective function that encapsulates the complex interplay of particle-matter interactions and physics analysis goals. In addition to a standard reconstruction-based metric commonly used in the field, we investigate the information-theoretic metric of mutual information. Unlike traditional methods, mutual information is inherently task-agnostic, offering a broader optimization paradigm that is less constrained by predefined targets. We demonstrate the effectiveness of our method in a realistic physics analysis scenario: optimizing the thicknesses of calorimeter detector layers based on simulated particle interactions. The surrogate model learns to approximate objective gradients, enabling efficient optimization with respect to energy resolution. Our findings reveal three key insights: (1) end-to-end black-box optimization using local surrogates is a practical and compelling approach for detector design, providing direct optimization of detector parameters in alignment with physics analysis goals; (2) mutual information-based optimization yields design choices that closely match those from state-of-the-art physics-informed methods, indicating that these approaches operate near optimality and reinforcing their reliability in HEP detector design; and (3) information-theoretic methods provide a powerful, generalizable framework for optimizing scientific instruments. By reframing the optimization process through an information-theoretic lens rather than domain-specific heuristics, mutual information enables the exploration of new avenues for discovery beyond conventional approaches.

TRANSIT your events into a new mass: Fast background interpolation for weakly-supervised anomaly searches

We introduce a new model for conditional and continuous data morphing called TRansport Adversarial Network for Smooth InTerpolation (TRANSIT). We apply it to create a background data template for weakly-supervised searches at the LHC. The method smoothly transforms sideband events to match signal region mass distributions. We demonstrate the performance of TRANSIT using the LHC Olympics R\&D dataset. The model captures non-linear mass correlations of features and produces a template that offers a competitive anomaly sensitivity compared to state-of-the-art transport-based template generators. Moreover, the computational training time required for TRANSIT is an order of magnitude lower than that of competing deep learning methods. This makes it ideal for analyses that iterate over many signal regions and signal models. Unlike generative models, which must learn a full probability density distribution, i.e., the correlations between all the variables, the proposed transport model only has to learn a smooth conditional shift of the distribution. This allows for a simpler, more efficient residual architecture, enabling mass uncorrelated features to pass the network unchanged while the mass correlated features are adjusted accordingly. Furthermore, we show that the latent space of the model provides a set of mass decorrelated features useful for anomaly detection without background sculpting.

Large Physics Models: Towards a collaborative approach with Large Language Models and Foundation Models

This paper explores ideas and provides a potential roadmap for the development and evaluation of physics-specific large-scale AI models, which we call Large Physics Models (LPMs). These models, based on foundation models such as Large Language Models (LLMs) - trained on broad data - are tailored to address the demands of physics research. LPMs can function independently or as part of an integrated framework. This framework can incorporate specialized tools, including symbolic reasoning modules for mathematical manipulations, frameworks to analyse specific experimental and simulated data, and mechanisms for synthesizing theories and scientific literature. We begin by examining whether the physics community should actively develop and refine dedicated models, rather than relying solely on commercial LLMs. We then outline how LPMs can be realized through interdisciplinary collaboration among experts in physics, computer science, and philosophy of science. To integrate these models effectively, we identify three key pillars: Development, Evaluation, and Philosophical Reflection. Development focuses on constructing models capable of processing physics texts, mathematical formulations, and diverse physical data. Evaluation assesses accuracy and reliability by testing and benchmarking. Finally, Philosophical Reflection encompasses the analysis of broader implications of LLMs in physics, including their potential to generate new scientific understanding and what novel collaboration dynamics might arise in research. Inspired by the organizational structure of experimental collaborations in particle physics, we propose a similarly interdisciplinary and collaborative approach to building and refining Large Physics Models. This roadmap provides specific objectives, defines pathways to achieve them, and identifies challenges that must be addressed to realise physics-specific large scale AI models.

Enhancing generalization in high energy physics using white-box adversarial attacks

Machine learning is becoming increasingly popular in the context of particle physics. Supervised learning, which uses labeled Monte Carlo (MC) simulations, remains one of the most widely used methods for discriminating signals beyond the Standard Model. However, this paper suggests that supervised models may depend excessively on artifacts and approximations from Monte Carlo simulations, potentially limiting their ability to generalize well to real data. This study aims to enhance the generalization properties of supervised models by reducing the sharpness of local minima. It reviews the application of four distinct white-box adversarial attacks in the context of classifying Higgs boson decay signals. The attacks are divided into weight space attacks, and feature space attacks. To study and quantify the sharpness of different local minima this paper presents two analysis methods: gradient ascent and reduced Hessian eigenvalue analysis. The results show that white-box adversarial attacks significantly improve generalization performance, albeit with increased computational complexity.

Variational inference for pile-up removal at hadron colliders with diffusion models

In this paper, we present a novel method for pile-up removal of pp interactions using variational inference with diffusion models, called Vipr. Instead of using classification methods to identify which particles are from the primary collision, a generative model is trained to predict the constituents of the hard-scatter particle jets with pile-up removed. This results in an estimate of the full posterior over hard-scatter jet constituents, which has not yet been explored in the context of pile-up removal. We evaluate the performance of Vipr in a sample of jets from simulated $t\bar{t}$ events overlain with pile-up contamination. Vipr outperforms SoftDrop in predicting the substructure of the hard-scatter jets over a wide range of pile-up scenarios.

PIPPIN: Generating variable length full events from partons

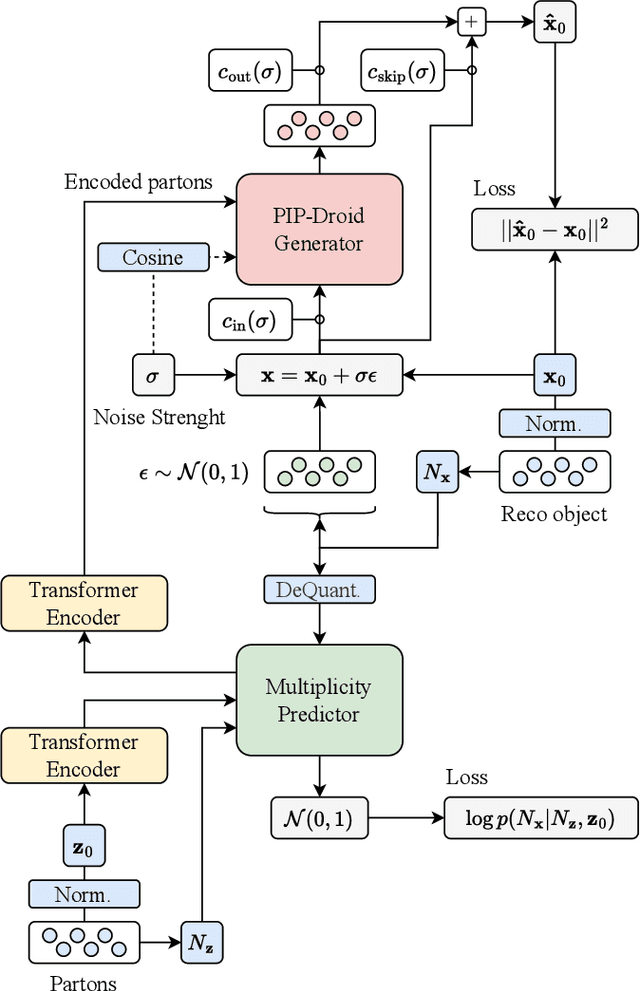
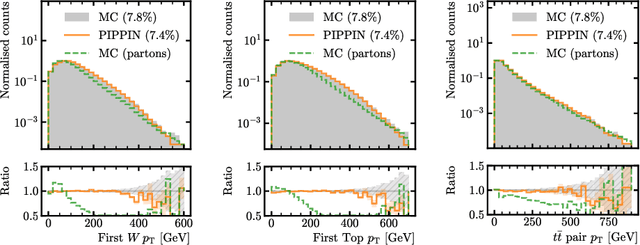
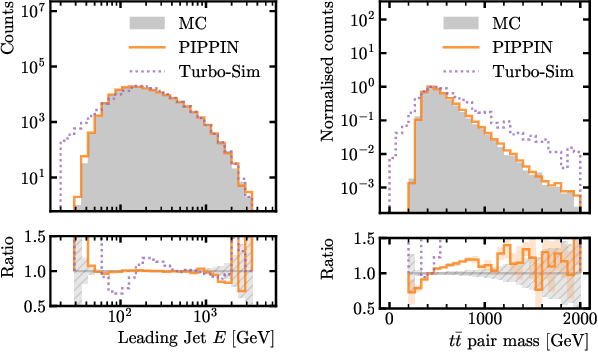
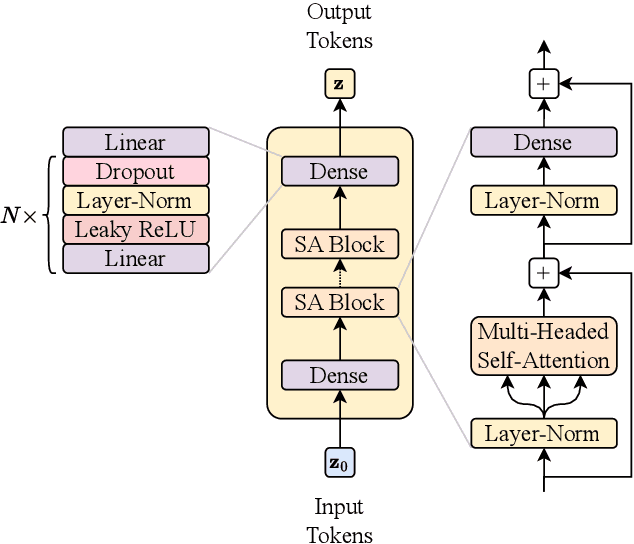
This paper presents a novel approach for directly generating full events at detector-level from parton-level information, leveraging cutting-edge machine learning techniques. To address the challenge of multiplicity variations between parton and reconstructed object spaces, we employ transformers, score-based models and normalizing flows. Our method tackles the inherent complexities of the stochastic transition between these two spaces and achieves remarkably accurate results. The combination of innovative techniques and the achieved accuracy demonstrates the potential of our approach in advancing the field and opens avenues for further exploration. This research contributes to the ongoing efforts in high-energy physics and generative modelling, providing a promising direction for enhanced precision in fast detector simulation.

Masked Particle Modeling on Sets: Towards Self-Supervised High Energy Physics Foundation Models

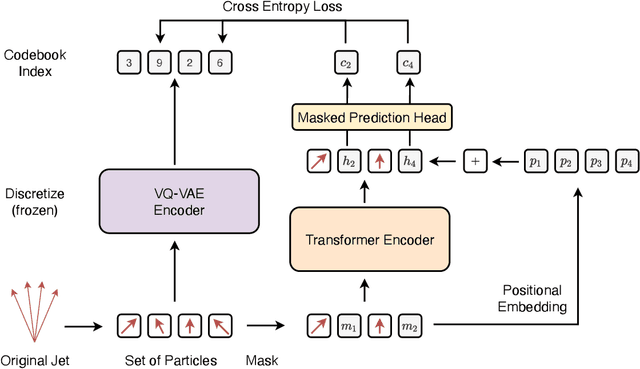
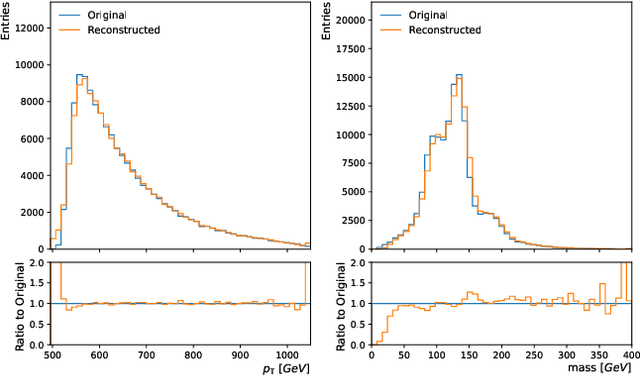
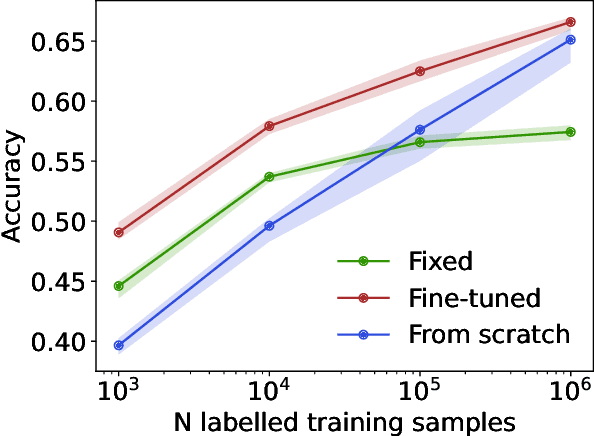
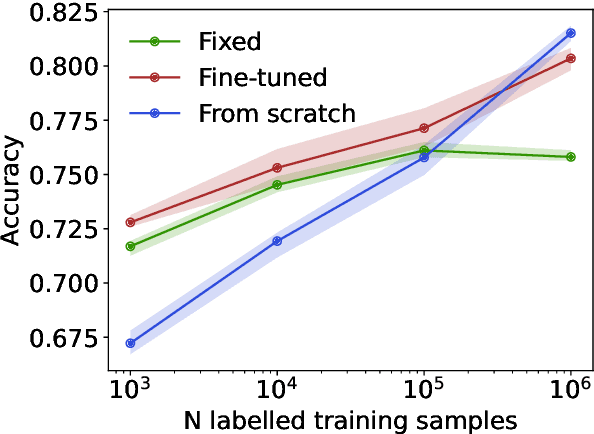
We propose masked particle modeling (MPM) as a self-supervised method for learning generic, transferable, and reusable representations on unordered sets of inputs for use in high energy physics (HEP) scientific data. This work provides a novel scheme to perform masked modeling based pre-training to learn permutation invariant functions on sets. More generally, this work provides a step towards building large foundation models for HEP that can be generically pre-trained with self-supervised learning and later fine-tuned for a variety of down-stream tasks. In MPM, particles in a set are masked and the training objective is to recover their identity, as defined by a discretized token representation of a pre-trained vector quantized variational autoencoder. We study the efficacy of the method in samples of high energy jets at collider physics experiments, including studies on the impact of discretization, permutation invariance, and ordering. We also study the fine-tuning capability of the model, showing that it can be adapted to tasks such as supervised and weakly supervised jet classification, and that the model can transfer efficiently with small fine-tuning data sets to new classes and new data domains.

Improving new physics searches with diffusion models for event observables and jet constituents

We introduce a new technique called Drapes to enhance the sensitivity in searches for new physics at the LHC. By training diffusion models on side-band data, we show how background templates for the signal region can be generated either directly from noise, or by partially applying the diffusion process to existing data. In the partial diffusion case, data can be drawn from side-band regions, with the inverse diffusion performed for new target conditional values, or from the signal region, preserving the distribution over the conditional property that defines the signal region. We apply this technique to the hunt for resonances using the LHCO di-jet dataset, and achieve state-of-the-art performance for background template generation using high level input features. We also show how Drapes can be applied to low level inputs with jet constituents, reducing the model dependence on the choice of input observables. Using jet constituents we can further improve sensitivity to the signal process, but observe a loss in performance where the signal significance before applying any selection is below 4$\sigma$.

EPiC-ly Fast Particle Cloud Generation with Flow-Matching and Diffusion

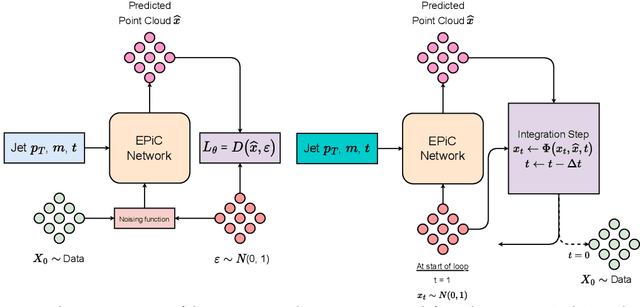
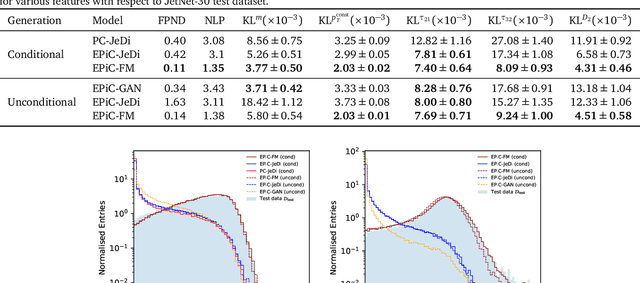
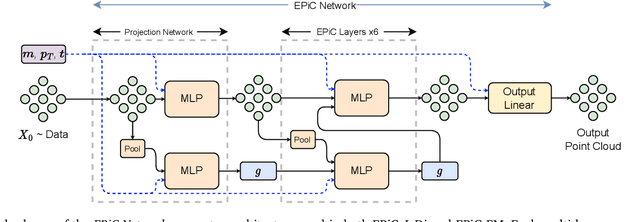
Jets at the LHC, typically consisting of a large number of highly correlated particles, are a fascinating laboratory for deep generative modeling. In this paper, we present two novel methods that generate LHC jets as point clouds efficiently and accurately. We introduce \epcjedi, which combines score-matching diffusion models with the Equivariant Point Cloud (EPiC) architecture based on the deep sets framework. This model offers a much faster alternative to previous transformer-based diffusion models without reducing the quality of the generated jets. In addition, we introduce \epcfm, the first permutation equivariant continuous normalizing flow (CNF) for particle cloud generation. This model is trained with {\it flow-matching}, a scalable and easy-to-train objective based on optimal transport that directly regresses the vector fields connecting the Gaussian noise prior to the data distribution. Our experiments demonstrate that \epcjedi and \epcfm both achieve state-of-the-art performance on the top-quark JetNet datasets whilst maintaining fast generation speed. Most notably, we find that the \epcfm model consistently outperforms all the other generative models considered here across every metric. Finally, we also introduce two new particle cloud performance metrics: the first based on the Kullback-Leibler divergence between feature distributions, the second is the negative log-posterior of a multi-model ParticleNet classifier.