Neuromorphic Readout for Hadron Calorimeters

We simulate hadrons impinging on a homogeneous lead-tungstate (PbWO4) calorimeter to investigate how the resulting light yield and its temporal structure, as detected by an array of light-sensitive sensors, can be processed by a neuromorphic computing system. Our model encodes temporal photon distributions as spike trains and employs a fully connected spiking neural network to estimate the total deposited energy, as well as the position and spatial distribution of the light emissions within the sensitive material. The extracted primitives offer valuable topological information about the shower development in the material, achieved without requiring a segmentation of the active medium. A potential nanophotonic implementation using III-V semiconductor nanowires is discussed. It can be both fast and energy efficient.

Unsupervised Particle Tracking with Neuromorphic Computing

We study the application of a neural network architecture for identifying charged particle trajectories via unsupervised learning of delays and synaptic weights using a spike-time-dependent plasticity rule. In the considered model, the neurons receive time-encoded information on the position of particle hits in a tracking detector for a particle collider, modeled according to the geometry of the Compact Muon Solenoid Phase II detector. We show how a spiking neural network is capable of successfully identifying in a completely unsupervised way the signal left by charged particles in the presence of conspicuous noise from accidental or combinatorial hits. These results open the way to applications of neuromorphic computing to particle tracking, motivating further studies into its potential for real-time, low-power particle tracking in future high-energy physics experiments.

Classification under Nuisance Parameters and Generalized Label Shift in Likelihood-Free Inference

An open scientific challenge is how to classify events with reliable measures of uncertainty, when we have a mechanistic model of the data-generating process but the distribution over both labels and latent nuisance parameters is different between train and target data. We refer to this type of distributional shift as generalized label shift (GLS). Direct classification using observed data $\mathbf{X}$ as covariates leads to biased predictions and invalid uncertainty estimates of labels $Y$. We overcome these biases by proposing a new method for robust uncertainty quantification that casts classification as a hypothesis testing problem under nuisance parameters. The key idea is to estimate the classifier's receiver operating characteristic (ROC) across the entire nuisance parameter space, which allows us to devise cutoffs that are invariant under GLS. Our method effectively endows a pre-trained classifier with domain adaptation capabilities and returns valid prediction sets while maintaining high power. We demonstrate its performance on two challenging scientific problems in biology and astroparticle physics with data from realistic mechanistic models.

TomOpt: Differential optimisation for task- and constraint-aware design of particle detectors in the context of muon tomography

We describe a software package, TomOpt, developed to optimise the geometrical layout and specifications of detectors designed for tomography by scattering of cosmic-ray muons. The software exploits differentiable programming for the modeling of muon interactions with detectors and scanned volumes, the inference of volume properties, and the optimisation cycle performing the loss minimisation. In doing so, we provide the first demonstration of end-to-end-differentiable and inference-aware optimisation of particle physics instruments. We study the performance of the software on a relevant benchmark scenarios and discuss its potential applications.

Simulation-Based Inference with WALDO: Perfectly Calibrated Confidence Regions Using Any Prediction or Posterior Estimation Algorithm

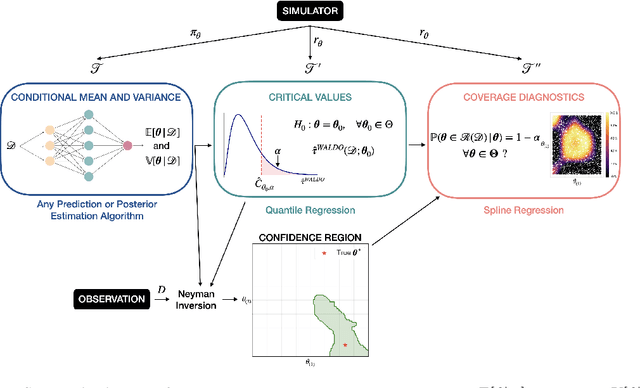
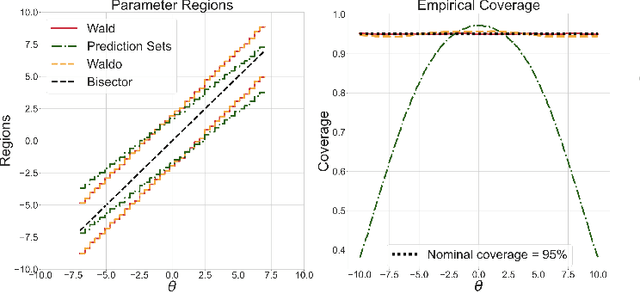
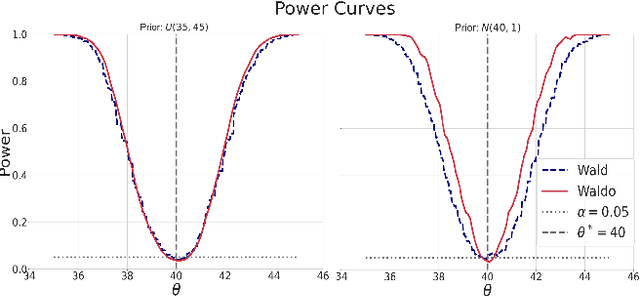
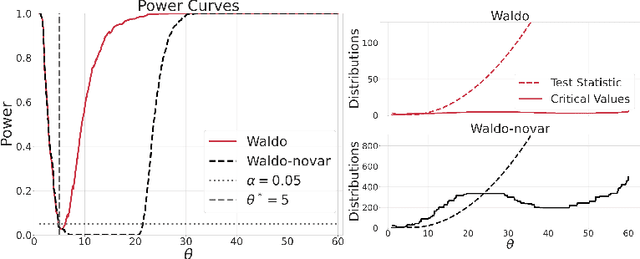
The vast majority of modern machine learning targets prediction problems, with algorithms such as Deep Neural Networks revolutionizing the accuracy of point predictions for high-dimensional complex data. Predictive approaches are now used in many domain sciences to directly estimate internal parameters of interest in theoretical simulator-based models. In parallel, common alternatives focus on estimating the full posterior using modern neural density estimators such as normalizing flows. However, an open problem in simulation-based inference (SBI) is how to construct properly calibrated confidence regions for internal parameters with nominal conditional coverage and high power. Many SBI methods are indeed known to produce overly confident posterior approximations, yielding misleading uncertainty estimates. Similarly, existing approaches for uncertainty quantification in deep learning provide no guarantees on conditional coverage. In this work, we present WALDO, a novel method for constructing correctly calibrated confidence regions in SBI. WALDO reframes the well-known Wald test and uses Neyman inversion to convert point predictions and posteriors from any prediction or posterior estimation algorithm to confidence sets with correct conditional coverage, even for finite sample sizes. As a concrete example, we demonstrate how a recently proposed deep learning prediction approach for particle energies in high-energy physics can be recalibrated using WALDO to produce confidence intervals with correct coverage and high power.

Advanced Multi-Variate Analysis Methods for New Physics Searches at the Large Hadron Collider

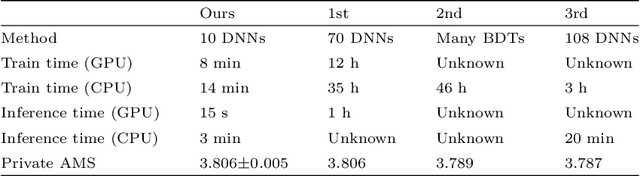
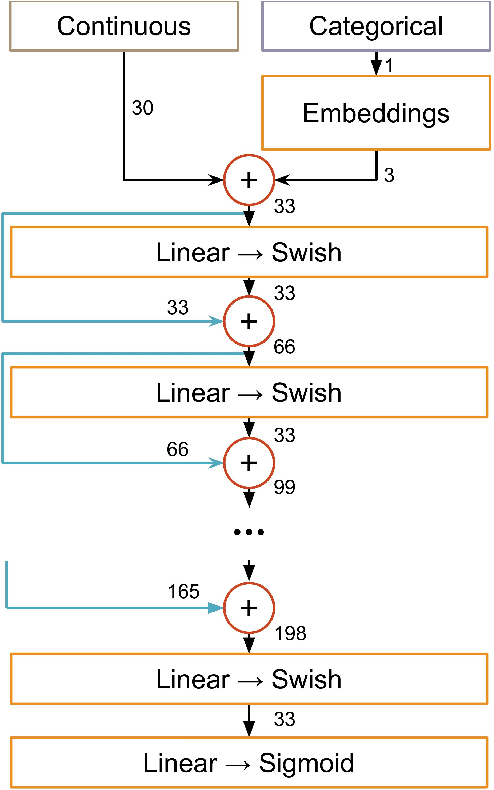
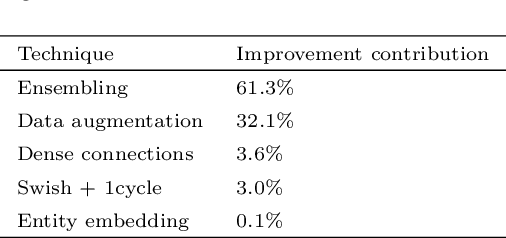
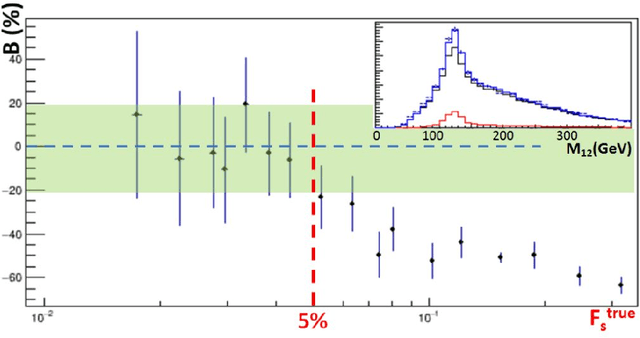
Between the years 2015 and 2019, members of the Horizon 2020-funded Innovative Training Network named "AMVA4NewPhysics" studied the customization and application of advanced multivariate analysis methods and statistical learning tools to high-energy physics problems, as well as developed entirely new ones. Many of those methods were successfully used to improve the sensitivity of data analyses performed by the ATLAS and CMS experiments at the CERN Large Hadron Collider; several others, still in the testing phase, promise to further improve the precision of measurements of fundamental physics parameters and the reach of searches for new phenomena. In this paper, the most relevant new tools, among those studied and developed, are presented along with the evaluation of their performances.

Dealing with Nuisance Parameters using Machine Learning in High Energy Physics: a Review

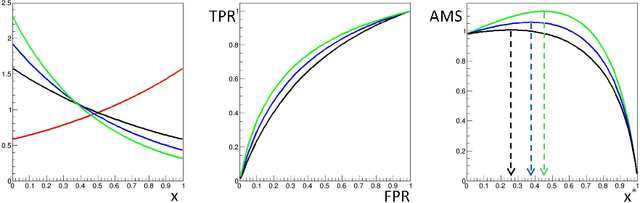
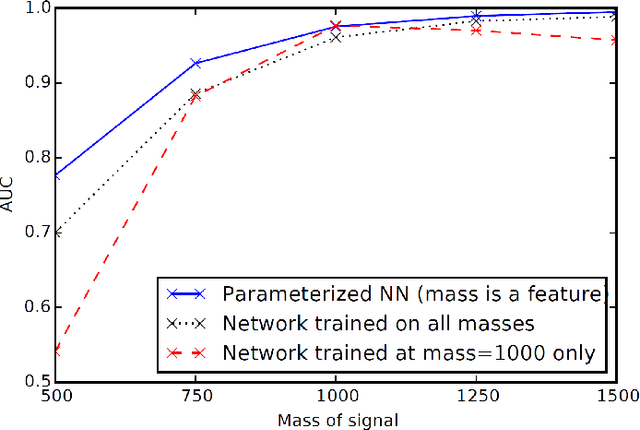
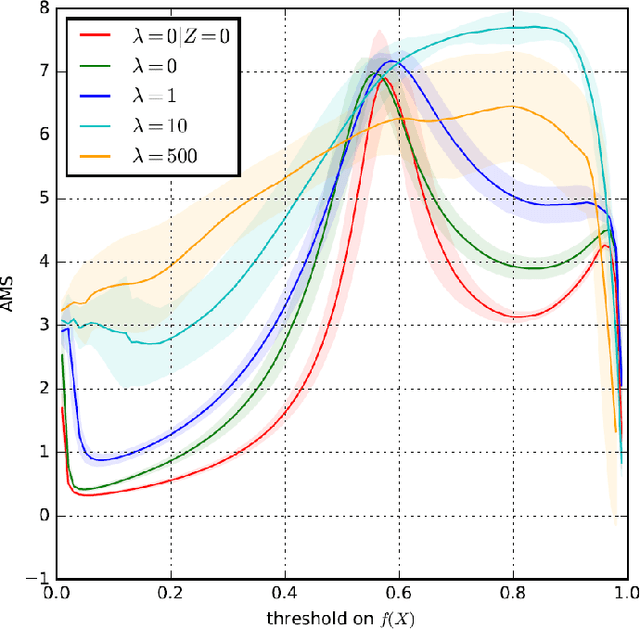
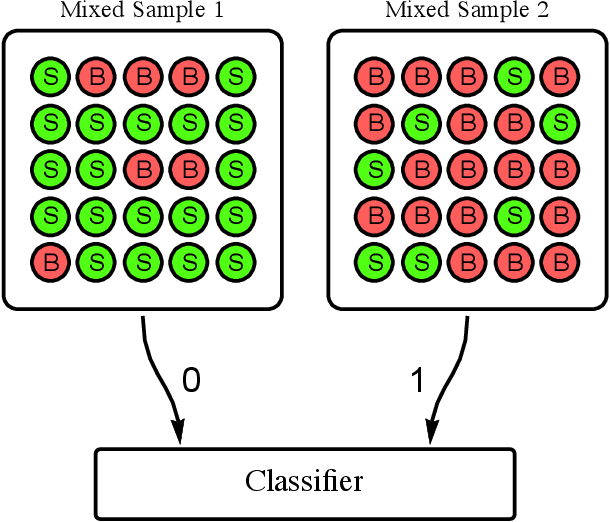
In this work we discuss the impact of nuisance parameters on the effectiveness of machine learning in high-energy physics problems, and provide a review of techniques that may reduce or remove their effect in the search for optimal selection criteria and variable transformations. Nuisance parameters often limit the usefulness of supervised learning in physical analyses due to the degradation of model performances in real data and/or the reduction of their statistical reach. The approaches discussed include nuisance-parametrized models, modified or adversary losses, semi-supervised learning approaches and inference-aware techniques.

INFERNO: Inference-Aware Neural Optimisation

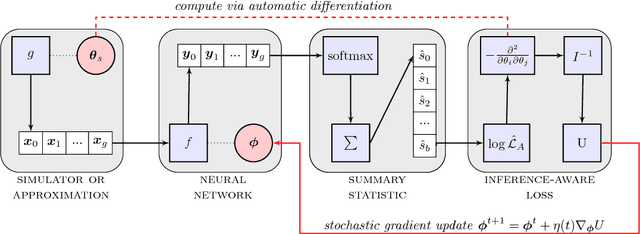
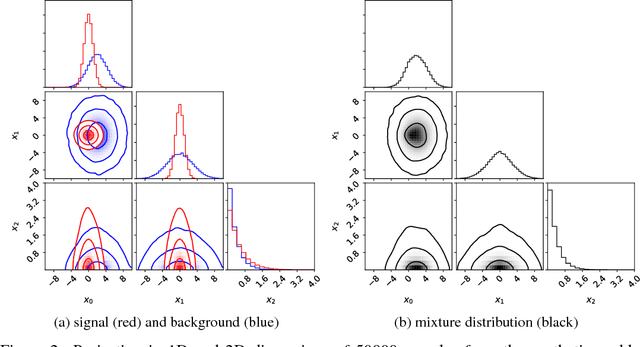
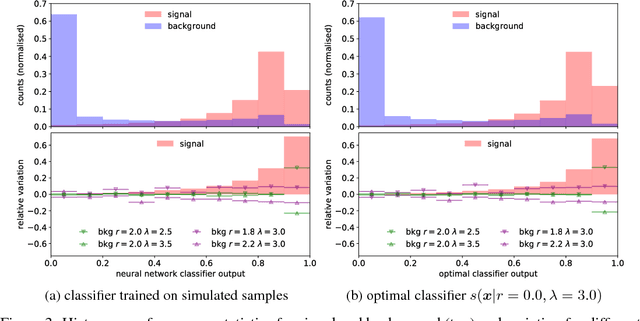
Complex computer simulations are commonly required for accurate data modelling in many scientific disciplines, making statistical inference challenging due to the intractability of the likelihood evaluation for the observed data. Furthermore, sometimes one is interested on inference drawn over a subset of the generative model parameters while taking into account model uncertainty or misspecification on the remaining nuisance parameters. In this work, we show how non-linear summary statistics can be constructed by minimising inference-motivated losses via stochastic gradient descent such they provided the smallest uncertainty for the parameters of interest. As a use case, the problem of confidence interval estimation for the mixture coefficient in a multi-dimensional two-component mixture model (i.e. signal vs background) is considered, where the proposed technique clearly outperforms summary statistics based on probabilistic classification, which are a commonly used alternative but do not account for the presence of nuisance parameters.

The Inverse Bagging Algorithm: Anomaly Detection by Inverse Bootstrap Aggregating

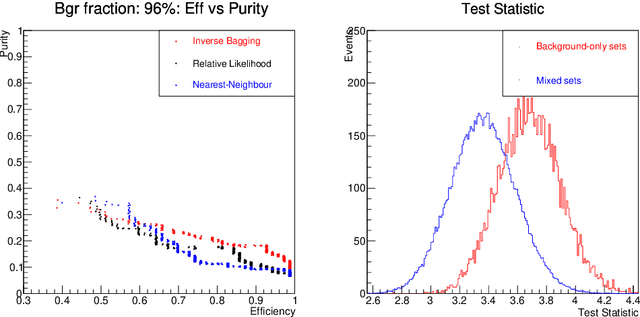
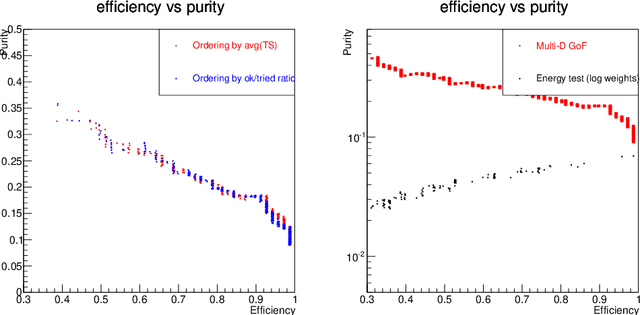
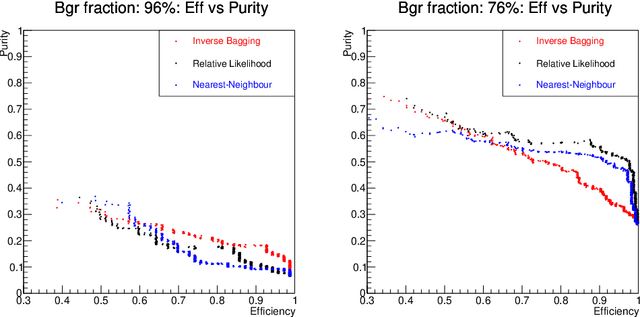
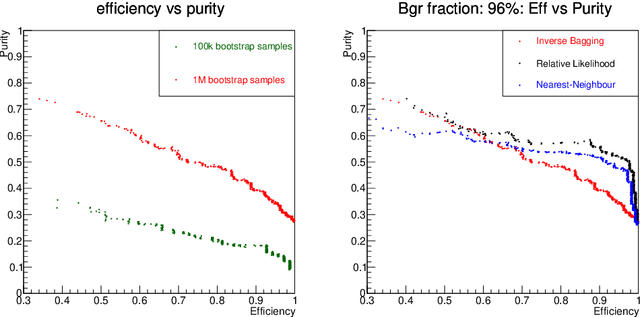
For data sets populated by a very well modeled process and by another process of unknown probability density function (PDF), a desired feature when manipulating the fraction of the unknown process (either for enhancing it or suppressing it) consists in avoiding to modify the kinematic distributions of the well modeled one. A bootstrap technique is used to identify sub-samples rich in the well modeled process, and classify each event according to the frequency of it being part of such sub-samples. Comparisons with general MVA algorithms will be shown, as well as a study of the asymptotic properties of the method, making use of a public domain data set that models a typical search for new physics as performed at hadronic colliders such as the Large Hadron Collider (LHC).