Enhancing Foundation Models for Time Series Forecasting via Wavelet-based Tokenization

How to best develop foundational models for time series forecasting remains an important open question. Tokenization is a crucial consideration in this effort: what is an effective discrete vocabulary for a real-valued sequential input? To address this question, we develop WaveToken, a wavelet-based tokenizer that allows models to learn complex representations directly in the space of time-localized frequencies. Our method first scales and decomposes the input time series, then thresholds and quantizes the wavelet coefficients, and finally pre-trains an autoregressive model to forecast coefficients for the forecast horizon. By decomposing coarse and fine structures in the inputs, wavelets provide an eloquent and compact language for time series forecasting that simplifies learning. Empirical results on a comprehensive benchmark, including 42 datasets for both in-domain and zero-shot settings, show that WaveToken: i) provides better accuracy than recently proposed foundation models for forecasting while using a much smaller vocabulary (1024 tokens), and performs on par or better than modern deep learning models trained specifically on each dataset; and ii) exhibits superior generalization capabilities, achieving the best average rank across all datasets for three complementary metrics. In addition, we show that our method can easily capture complex temporal patterns of practical relevance that are challenging for other recent pre-trained models, including trends, sparse spikes, and non-stationary time series with varying frequencies evolving over time.

Classification under Nuisance Parameters and Generalized Label Shift in Likelihood-Free Inference

An open scientific challenge is how to classify events with reliable measures of uncertainty, when we have a mechanistic model of the data-generating process but the distribution over both labels and latent nuisance parameters is different between train and target data. We refer to this type of distributional shift as generalized label shift (GLS). Direct classification using observed data $\mathbf{X}$ as covariates leads to biased predictions and invalid uncertainty estimates of labels $Y$. We overcome these biases by proposing a new method for robust uncertainty quantification that casts classification as a hypothesis testing problem under nuisance parameters. The key idea is to estimate the classifier's receiver operating characteristic (ROC) across the entire nuisance parameter space, which allows us to devise cutoffs that are invariant under GLS. Our method effectively endows a pre-trained classifier with domain adaptation capabilities and returns valid prediction sets while maintaining high power. We demonstrate its performance on two challenging scientific problems in biology and astroparticle physics with data from realistic mechanistic models.

Adaptive Sampling for Probabilistic Forecasting under Distribution Shift

The world is not static: This causes real-world time series to change over time through external, and potentially disruptive, events such as macroeconomic cycles or the COVID-19 pandemic. We present an adaptive sampling strategy that selects the part of the time series history that is relevant for forecasting. We achieve this by learning a discrete distribution over relevant time steps by Bayesian optimization. We instantiate this idea with a two-step method that is pre-trained with uniform sampling and then training a lightweight adaptive architecture with adaptive sampling. We show with synthetic and real-world experiments that this method adapts to distribution shift and significantly reduces the forecasting error of the base model for three out of five datasets.

Simulation-Based Inference with WALDO: Perfectly Calibrated Confidence Regions Using Any Prediction or Posterior Estimation Algorithm

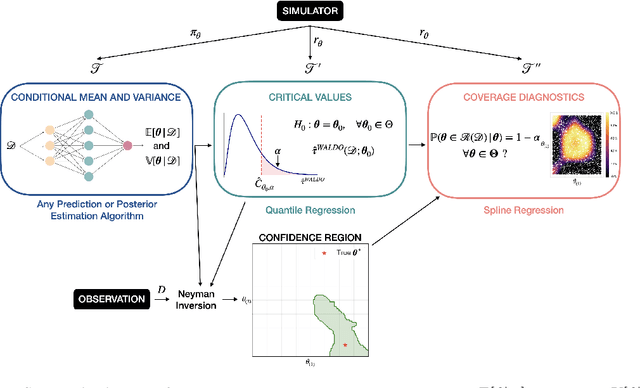
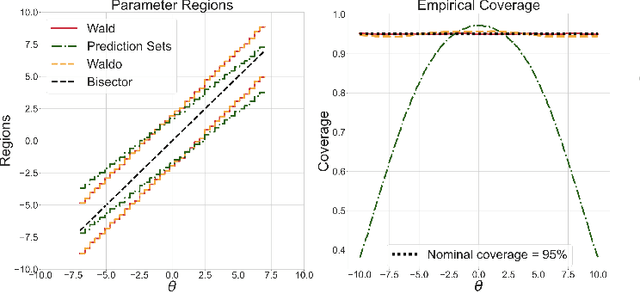
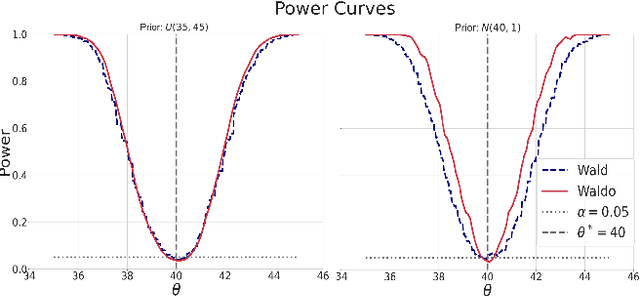
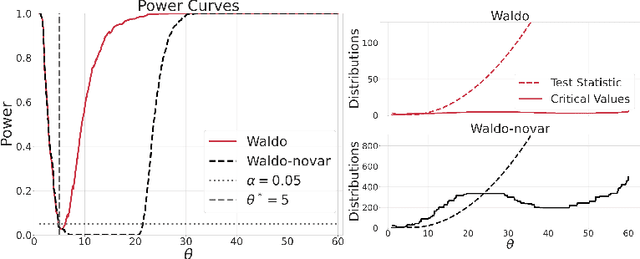
The vast majority of modern machine learning targets prediction problems, with algorithms such as Deep Neural Networks revolutionizing the accuracy of point predictions for high-dimensional complex data. Predictive approaches are now used in many domain sciences to directly estimate internal parameters of interest in theoretical simulator-based models. In parallel, common alternatives focus on estimating the full posterior using modern neural density estimators such as normalizing flows. However, an open problem in simulation-based inference (SBI) is how to construct properly calibrated confidence regions for internal parameters with nominal conditional coverage and high power. Many SBI methods are indeed known to produce overly confident posterior approximations, yielding misleading uncertainty estimates. Similarly, existing approaches for uncertainty quantification in deep learning provide no guarantees on conditional coverage. In this work, we present WALDO, a novel method for constructing correctly calibrated confidence regions in SBI. WALDO reframes the well-known Wald test and uses Neyman inversion to convert point predictions and posteriors from any prediction or posterior estimation algorithm to confidence sets with correct conditional coverage, even for finite sample sizes. As a concrete example, we demonstrate how a recently proposed deep learning prediction approach for particle energies in high-energy physics can be recalibrated using WALDO to produce confidence intervals with correct coverage and high power.