Simulation-Based Inference with WALDO: Perfectly Calibrated Confidence Regions Using Any Prediction or Posterior Estimation Algorithm

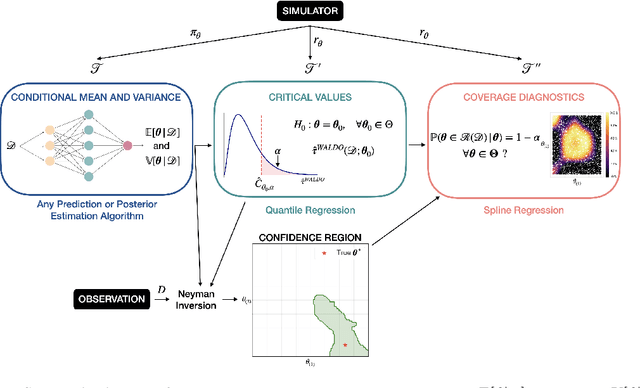
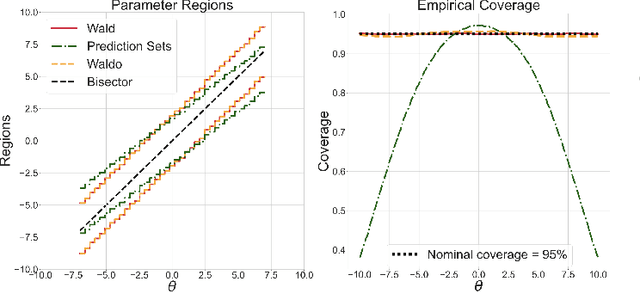
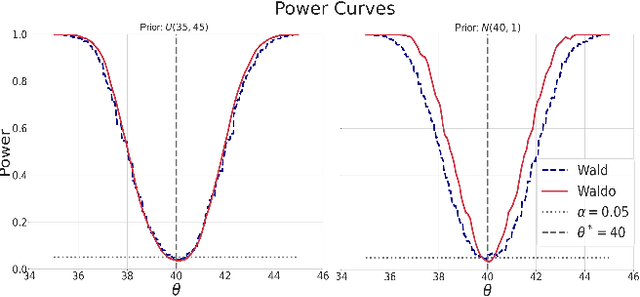
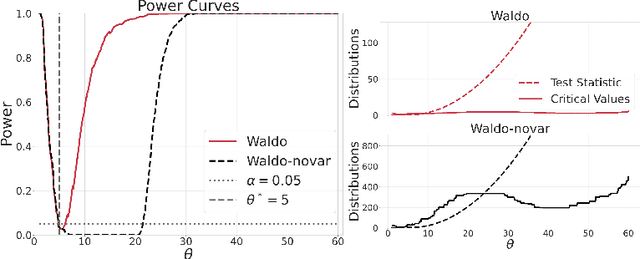
The vast majority of modern machine learning targets prediction problems, with algorithms such as Deep Neural Networks revolutionizing the accuracy of point predictions for high-dimensional complex data. Predictive approaches are now used in many domain sciences to directly estimate internal parameters of interest in theoretical simulator-based models. In parallel, common alternatives focus on estimating the full posterior using modern neural density estimators such as normalizing flows. However, an open problem in simulation-based inference (SBI) is how to construct properly calibrated confidence regions for internal parameters with nominal conditional coverage and high power. Many SBI methods are indeed known to produce overly confident posterior approximations, yielding misleading uncertainty estimates. Similarly, existing approaches for uncertainty quantification in deep learning provide no guarantees on conditional coverage. In this work, we present WALDO, a novel method for constructing correctly calibrated confidence regions in SBI. WALDO reframes the well-known Wald test and uses Neyman inversion to convert point predictions and posteriors from any prediction or posterior estimation algorithm to confidence sets with correct conditional coverage, even for finite sample sizes. As a concrete example, we demonstrate how a recently proposed deep learning prediction approach for particle energies in high-energy physics can be recalibrated using WALDO to produce confidence intervals with correct coverage and high power.