INFERNO: Inference-Aware Neural Optimisation
Paper and Code
Oct 11, 2018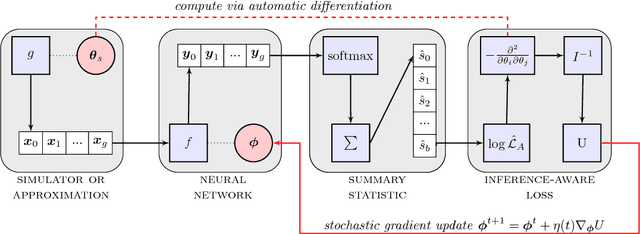

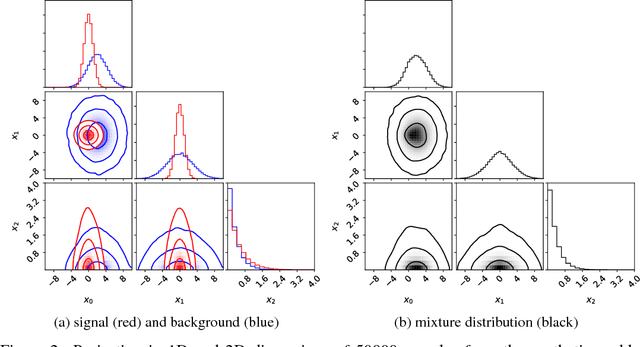
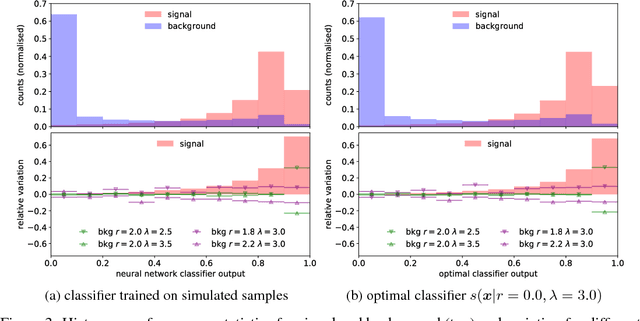
Complex computer simulations are commonly required for accurate data modelling in many scientific disciplines, making statistical inference challenging due to the intractability of the likelihood evaluation for the observed data. Furthermore, sometimes one is interested on inference drawn over a subset of the generative model parameters while taking into account model uncertainty or misspecification on the remaining nuisance parameters. In this work, we show how non-linear summary statistics can be constructed by minimising inference-motivated losses via stochastic gradient descent such they provided the smallest uncertainty for the parameters of interest. As a use case, the problem of confidence interval estimation for the mixture coefficient in a multi-dimensional two-component mixture model (i.e. signal vs background) is considered, where the proposed technique clearly outperforms summary statistics based on probabilistic classification, which are a commonly used alternative but do not account for the presence of nuisance parameters.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge