Advanced Multi-Variate Analysis Methods for New Physics Searches at the Large Hadron Collider

Between the years 2015 and 2019, members of the Horizon 2020-funded Innovative Training Network named "AMVA4NewPhysics" studied the customization and application of advanced multivariate analysis methods and statistical learning tools to high-energy physics problems, as well as developed entirely new ones. Many of those methods were successfully used to improve the sensitivity of data analyses performed by the ATLAS and CMS experiments at the CERN Large Hadron Collider; several others, still in the testing phase, promise to further improve the precision of measurements of fundamental physics parameters and the reach of searches for new phenomena. In this paper, the most relevant new tools, among those studied and developed, are presented along with the evaluation of their performances.

Dealing with Nuisance Parameters using Machine Learning in High Energy Physics: a Review

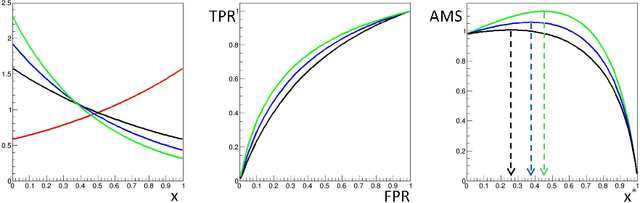
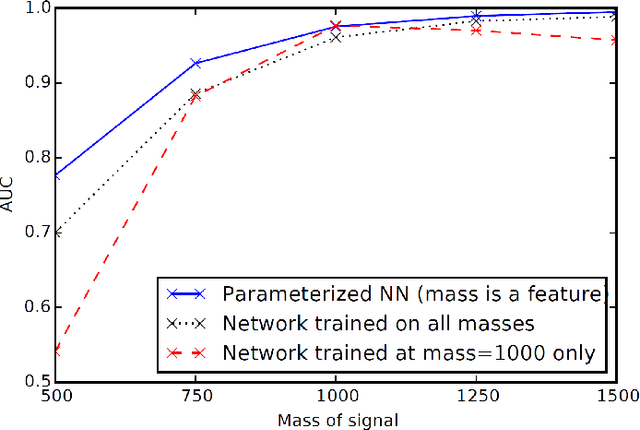
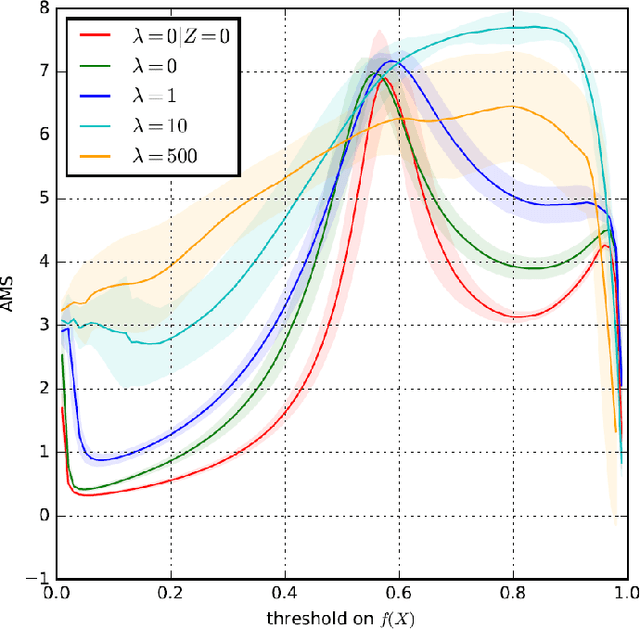
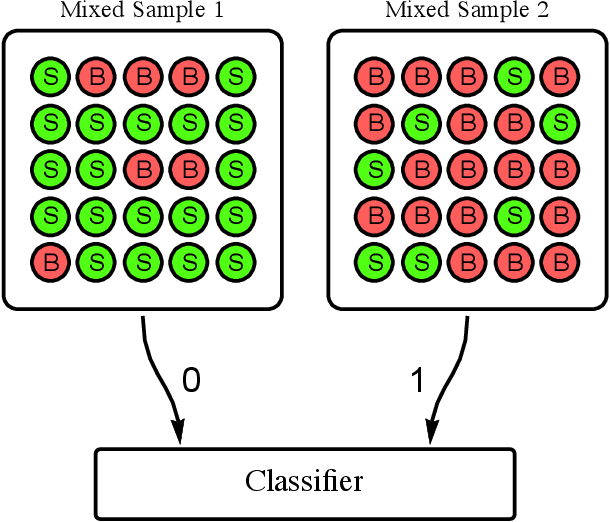
In this work we discuss the impact of nuisance parameters on the effectiveness of machine learning in high-energy physics problems, and provide a review of techniques that may reduce or remove their effect in the search for optimal selection criteria and variable transformations. Nuisance parameters often limit the usefulness of supervised learning in physical analyses due to the degradation of model performances in real data and/or the reduction of their statistical reach. The approaches discussed include nuisance-parametrized models, modified or adversary losses, semi-supervised learning approaches and inference-aware techniques.

INFERNO: Inference-Aware Neural Optimisation

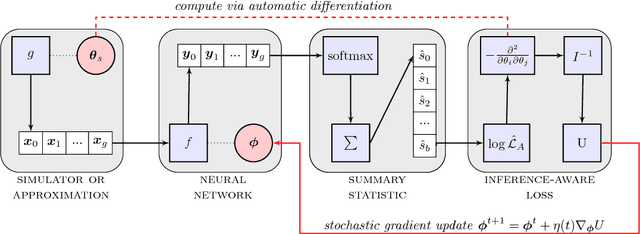
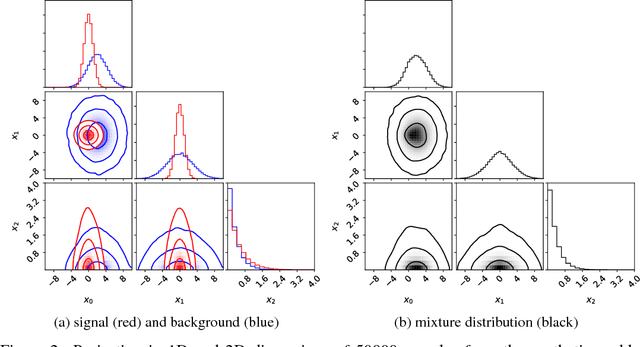
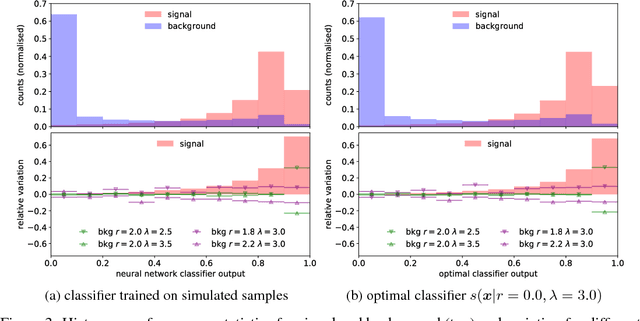
Complex computer simulations are commonly required for accurate data modelling in many scientific disciplines, making statistical inference challenging due to the intractability of the likelihood evaluation for the observed data. Furthermore, sometimes one is interested on inference drawn over a subset of the generative model parameters while taking into account model uncertainty or misspecification on the remaining nuisance parameters. In this work, we show how non-linear summary statistics can be constructed by minimising inference-motivated losses via stochastic gradient descent such they provided the smallest uncertainty for the parameters of interest. As a use case, the problem of confidence interval estimation for the mixture coefficient in a multi-dimensional two-component mixture model (i.e. signal vs background) is considered, where the proposed technique clearly outperforms summary statistics based on probabilistic classification, which are a commonly used alternative but do not account for the presence of nuisance parameters.