Beyond Ansätze: Learning Quantum Circuits as Unitary Operators

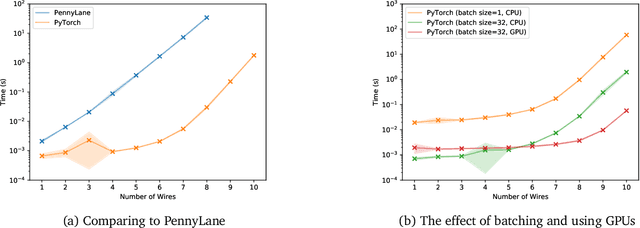
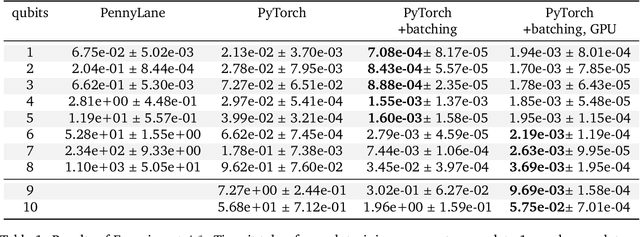
This paper explores the advantages of optimizing quantum circuits on $N$ wires as operators in the unitary group $U(2^N)$. We run gradient-based optimization in the Lie algebra $\mathfrak u(2^N)$ and use the exponential map to parametrize unitary matrices. We argue that $U(2^N)$ is not only more general than the search space induced by an ansatz, but in ways easier to work with on classical computers. The resulting approach is quick, ansatz-free and provides an upper bound on performance over all ans\"atze on $N$ wires.

Quantum versus Classical Generative Modelling in Finance

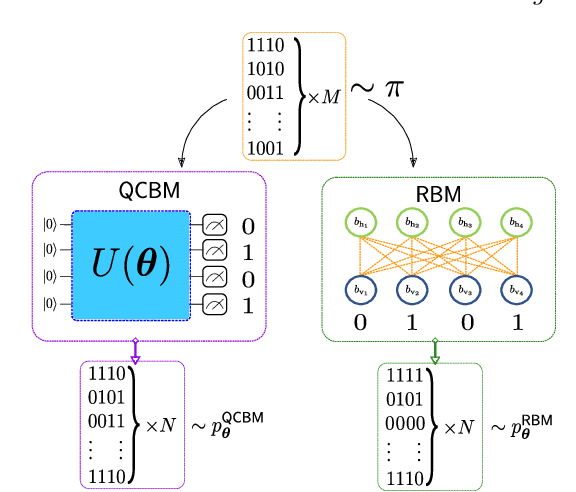
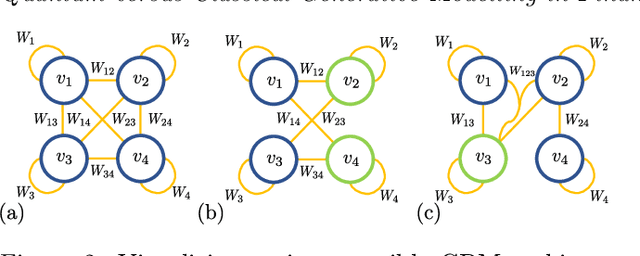
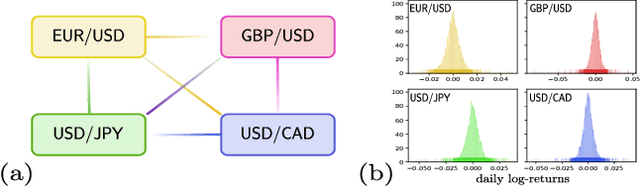
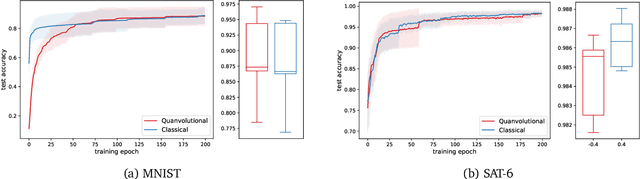
Finding a concrete use case for quantum computers in the near term is still an open question, with machine learning typically touted as one of the first fields which will be impacted by quantum technologies. In this work, we investigate and compare the capabilities of quantum versus classical models for the task of generative modelling in machine learning. We use a real world financial dataset consisting of correlated currency pairs and compare two models in their ability to learn the resulting distribution - a restricted Boltzmann machine, and a quantum circuit Born machine. We provide extensive numerical results indicating that the simulated Born machine always at least matches the performance of the Boltzmann machine in this task, and demonstrates superior performance as the model scales. We perform experiments on both simulated and physical quantum chips using the Rigetti forest platform, and also are able to partially train the largest instance to date of a quantum circuit Born machine on quantum hardware. Finally, by studying the entanglement capacity of the training Born machines, we find that entanglement typically plays a role in the problem instances which demonstrate an advantage over the Boltzmann machine.

Leveraging Adiabatic Quantum Computation for Election Forecasting

Accurate, reliable sampling from fully-connected graphs with arbitrary correlations is a difficult problem. Such sampling requires knowledge of the probabilities of observing every possible state of a graph. As graph size grows, the number of model states becomes intractably large and efficient computation requires full sampling be replaced with heuristics and algorithms that are only approximations of full sampling. This work investigates the potential impact of adiabatic quantum computation for sampling purposes, building on recent successes training Boltzmann machines using a quantum device. We investigate the use case of quantum computation to train Boltzmann machines for predicting the 2016 Presidential election.