Agnostic Process Tomography

Characterizing a quantum system by learning its state or evolution is a fundamental problem in quantum physics and learning theory with a myriad of applications. Recently, as a new approach to this problem, the task of agnostic state tomography was defined, in which one aims to approximate an arbitrary quantum state by a simpler one in a given class. Generalizing this notion to quantum processes, we initiate the study of agnostic process tomography: given query access to an unknown quantum channel $\Phi$ and a known concept class $\mathcal{C}$ of channels, output a quantum channel that approximates $\Phi$ as well as any channel in the concept class $\mathcal{C}$, up to some error. In this work, we propose several natural applications for this new task in quantum machine learning, quantum metrology, classical simulation, and error mitigation. In addition, we give efficient agnostic process tomography algorithms for a wide variety of concept classes, including Pauli strings, Pauli channels, quantum junta channels, low-degree channels, and a class of channels produced by $\mathsf{QAC}^0$ circuits. The main technical tool we use is Pauli spectrum analysis of operators and superoperators. We also prove that, using ancilla qubits, any agnostic state tomography algorithm can be extended to one solving agnostic process tomography for a compatible concept class of unitaries, immediately giving us efficient agnostic learning algorithms for Clifford circuits, Clifford circuits with few T gates, and circuits consisting of a tensor product of single-qubit gates. Together, our results provide insight into the conditions and new algorithms necessary to extend the learnability of a concept class from the standard tomographic setting to the agnostic one.

A unifying framework for differentially private quantum algorithms

Differential privacy is a widely used notion of security that enables the processing of sensitive information. In short, differentially private algorithms map "neighbouring" inputs to close output distributions. Prior work proposed several quantum extensions of differential privacy, each of them built on substantially different notions of neighbouring quantum states. In this paper, we propose a novel and general definition of neighbouring quantum states. We demonstrate that this definition captures the underlying structure of quantum encodings and can be used to provide exponentially tighter privacy guarantees for quantum measurements. Our approach combines the addition of classical and quantum noise and is motivated by the noisy nature of near-term quantum devices. Moreover, we also investigate an alternative setting where we are provided with multiple copies of the input state. In this case, differential privacy can be ensured with little loss in accuracy combining concentration of measure and noise-adding mechanisms. En route, we prove the advanced joint convexity of the quantum hockey-stick divergence and we demonstrate how this result can be applied to quantum differential privacy. Finally, we complement our theoretical findings with an empirical estimation of the certified adversarial robustness ensured by differentially private measurements.

Differential Privacy Amplification in Quantum and Quantum-inspired Algorithms

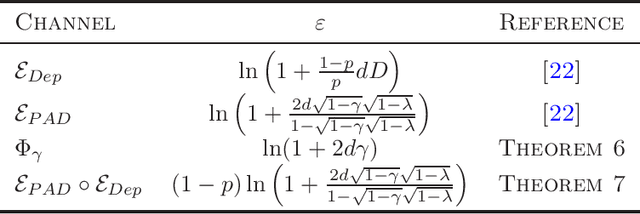
Differential privacy provides a theoretical framework for processing a dataset about $n$ users, in a way that the output reveals a minimal information about any single user. Such notion of privacy is usually ensured by noise-adding mechanisms and amplified by several processes, including subsampling, shuffling, iteration, mixing and diffusion. In this work, we provide privacy amplification bounds for quantum and quantum-inspired algorithms. In particular, we show for the first time, that algorithms running on quantum encoding of a classical dataset or the outcomes of quantum-inspired classical sampling, amplify differential privacy. Moreover, we prove that a quantum version of differential privacy is amplified by the composition of quantum channels, provided that they satisfy some mixing conditions.

Quantum Local Differential Privacy and Quantum Statistical Query Model

The problem of private learning has been extensively studied in classical computer science. Notably, a striking equivalence between local differentially private learning and statistical query learning has been shown. In addition, the statistical query model has been recently extended to quantum computation. In this work, we give a formal definition of quantum local differential privacy and we extend the aforementioned result to quantum computation.

Graph neural network initialisation of quantum approximate optimisation

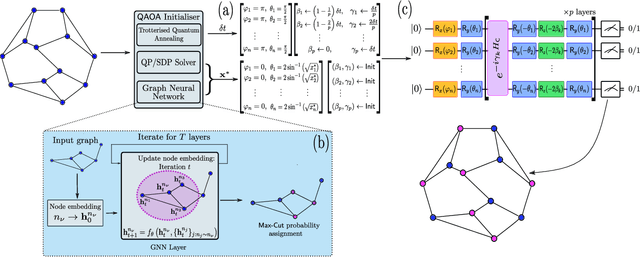
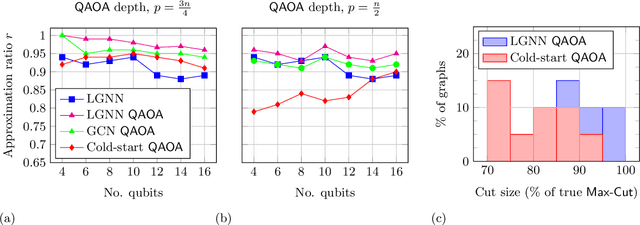
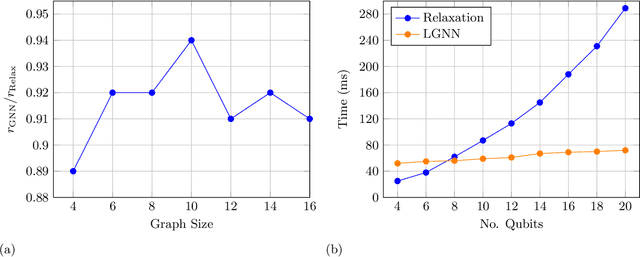
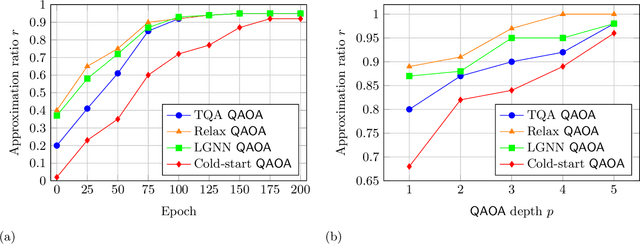
Approximate combinatorial optimisation has emerged as one of the most promising application areas for quantum computers, particularly those in the near term. In this work, we focus on the quantum approximate optimisation algorithm (QAOA) for solving the Max-Cut problem. Specifically, we address two problems in the QAOA, how to select initial parameters, and how to subsequently train the parameters to find an optimal solution. For the former, we propose graph neural networks (GNNs) as an initialisation routine for the QAOA parameters, adding to the literature on warm-starting techniques. We show the GNN approach generalises across not only graph instances, but also to increasing graph sizes, a feature not available to other warm-starting techniques. For training the QAOA, we test several optimisers for the MaxCut problem. These include quantum aware/agnostic optimisers proposed in literature and we also incorporate machine learning techniques such as reinforcement and meta-learning. With the incorporation of these initialisation and optimisation toolkits, we demonstrate how the QAOA can be trained as an end-to-end differentiable pipeline.

Variational Quantum Cloning: Improving Practicality for Quantum Cryptanalysis

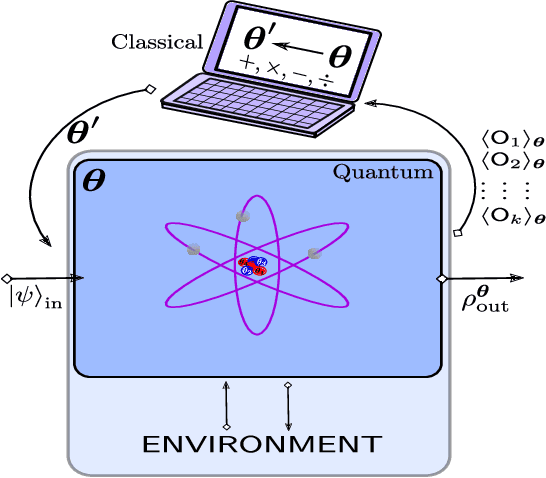
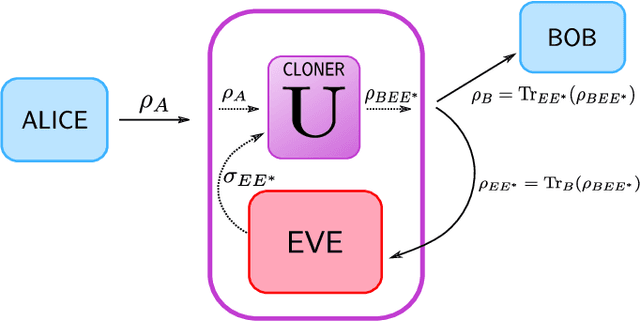
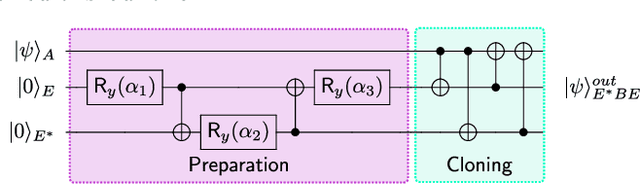
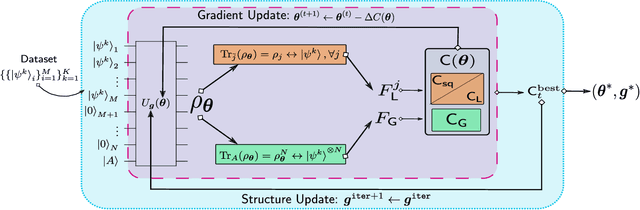
Cryptanalysis on standard quantum cryptographic systems generally involves finding optimal adversarial attack strategies on the underlying protocols. The core principle of modelling quantum attacks in many cases reduces to the adversary's ability to clone unknown quantum states which facilitates the extraction of some meaningful secret information. Explicit optimal attack strategies typically require high computational resources due to large circuit depths or, in many cases, are unknown. In this work, we propose variational quantum cloning (VQC), a quantum machine learning based cryptanalysis algorithm which allows an adversary to obtain optimal (approximate) cloning strategies with short depth quantum circuits, trained using hybrid classical-quantum techniques. The algorithm contains operationally meaningful cost functions with theoretical guarantees, quantum circuit structure learning and gradient descent based optimisation. Our approach enables the end-to-end discovery of hardware efficient quantum circuits to clone specific families of quantum states, which in turn leads to an improvement in cloning fidelites when implemented on quantum hardware: the Rigetti Aspen chip. Finally, we connect these results to quantum cryptographic primitives, in particular quantum coin flipping. We derive attacks on two protocols as examples, based on quantum cloning and facilitated by VQC. As a result, our algorithm can improve near term attacks on these protocols, using approximate quantum cloning as a resource.

Quantum versus Classical Generative Modelling in Finance

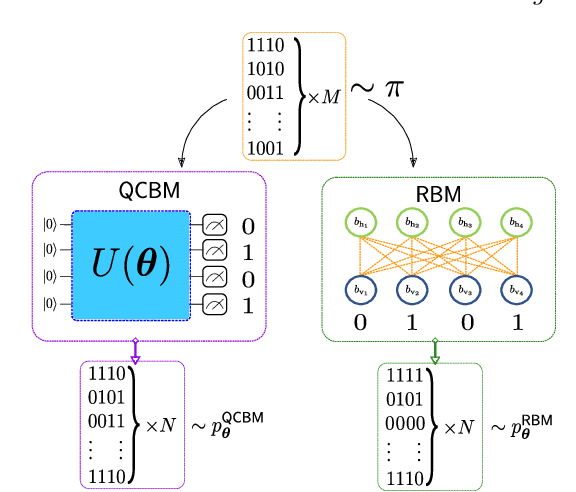
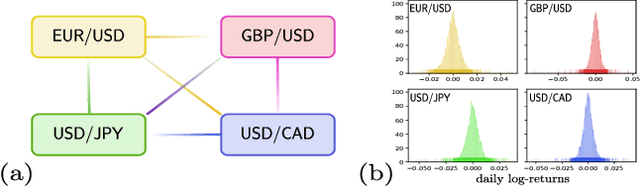
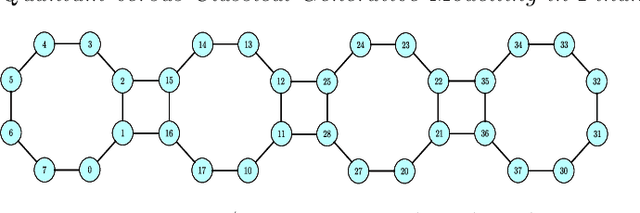
Finding a concrete use case for quantum computers in the near term is still an open question, with machine learning typically touted as one of the first fields which will be impacted by quantum technologies. In this work, we investigate and compare the capabilities of quantum versus classical models for the task of generative modelling in machine learning. We use a real world financial dataset consisting of correlated currency pairs and compare two models in their ability to learn the resulting distribution - a restricted Boltzmann machine, and a quantum circuit Born machine. We provide extensive numerical results indicating that the simulated Born machine always at least matches the performance of the Boltzmann machine in this task, and demonstrates superior performance as the model scales. We perform experiments on both simulated and physical quantum chips using the Rigetti forest platform, and also are able to partially train the largest instance to date of a quantum circuit Born machine on quantum hardware. Finally, by studying the entanglement capacity of the training Born machines, we find that entanglement typically plays a role in the problem instances which demonstrate an advantage over the Boltzmann machine.

The Born Supremacy: Quantum Advantage and Training of an Ising Born Machine

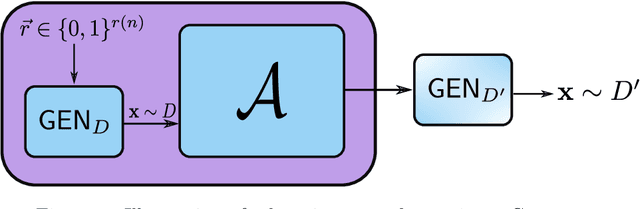
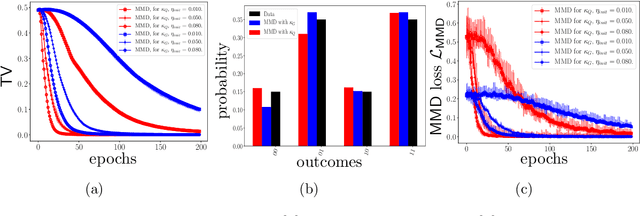
The search for an application of near-term quantum devices is widespread. Quantum Machine Learning is touted as a potential utilisation of such devices, particularly those which are out of the reach of the simulation capabilities of classical computers. In this work, we propose a generative Quantum Machine Learning Model, called the Ising Born Machine (IBM), which we show cannot, in the worst case, and up to suitable notions of error, be simulated efficiently by a classical device. We also show this holds for all the circuit families encountered during training. In particular, we explore quantum circuit learning using non-universal circuits derived from Ising Model Hamiltonians, which are implementable on near term quantum devices. We propose two novel training methods for the IBM by utilising the Stein Discrepancy and the Sinkhorn Divergence cost functions. We show numerically, both using a simulator within Rigetti's Forest platform and on the Aspen-1 16Q chip, that the cost functions we suggest outperform the more commonly used Maximum Mean Discrepancy (MMD) for differentiable training. We also propose an improvement to the MMD by proposing a novel utilisation of quantum kernels which we demonstrate provides improvements over its classical counterpart. We discuss the potential of these methods to learn `hard' quantum distributions, a feat which would demonstrate the advantage of quantum over classical computers, and provide the first formal definitions for what we call `Quantum Learning Supremacy'. Finally, we propose a novel view on the area of quantum circuit compilation by using the IBM to `mimic' target quantum circuits using classical output data only.