Efficient quantum-enhanced classical simulation for patches of quantum landscapes

Understanding the capabilities of classical simulation methods is key to identifying where quantum computers are advantageous. Not only does this ensure that quantum computers are used only where necessary, but also one can potentially identify subroutines that can be offloaded onto a classical device. In this work, we show that it is always possible to generate a classical surrogate of a sub-region (dubbed a "patch") of an expectation landscape produced by a parameterized quantum circuit. That is, we provide a quantum-enhanced classical algorithm which, after simple measurements on a quantum device, allows one to classically simulate approximate expectation values of a subregion of a landscape. We provide time and sample complexity guarantees for a range of families of circuits of interest, and further numerically demonstrate our simulation algorithms on an exactly verifiable simulation of a Hamiltonian variational ansatz and long-time dynamics simulation on a 127-qubit heavy-hex topology.

Learning unitaries with quantum statistical queries

We propose several algorithms for learning unitary operators from quantum statistical queries (QSQs) with respect to their Choi-Jamiolkowski state. Quantum statistical queries capture the capabilities of a learner with limited quantum resources, which receives as input only noisy estimates of expected values of measurements. Our methods hinge on a novel technique for estimating the Fourier mass of a unitary on a subset of Pauli strings with a single quantum statistical query, generalizing a previous result for uniform quantum examples. Exploiting this insight, we show that the quantum Goldreich-Levin algorithm can be implemented with quantum statistical queries, whereas the prior version of the algorithm involves oracle access to the unitary and its inverse. Moreover, we prove that $\mathcal{O}(\log n)$-juntas and quantum Boolean functions with constant total influence are efficiently learnable in our model, and constant-depth circuits are learnable sample-efficiently with quantum statistical queries. On the other hand, all previous algorithms for these tasks require direct access to the Choi-Jamiolkowski state or oracle access to the unitary. In addition, our upper bounds imply that the actions of those classes of unitaries on locally scrambled ensembles can be efficiently learned. We also demonstrate that, despite these positive results, quantum statistical queries lead to an exponentially larger sample complexity for certain tasks, compared to separable measurements to the Choi-Jamiolkowski state. In particular, we show an exponential lower bound for learning a class of phase-oracle unitaries and a double exponential lower bound for testing the unitarity of channels, adapting to our setting previous arguments for quantum states. Finally, we propose a new definition of average-case surrogate models, showing a potential application of our results to hybrid quantum machine learning.

A unifying framework for differentially private quantum algorithms

Differential privacy is a widely used notion of security that enables the processing of sensitive information. In short, differentially private algorithms map "neighbouring" inputs to close output distributions. Prior work proposed several quantum extensions of differential privacy, each of them built on substantially different notions of neighbouring quantum states. In this paper, we propose a novel and general definition of neighbouring quantum states. We demonstrate that this definition captures the underlying structure of quantum encodings and can be used to provide exponentially tighter privacy guarantees for quantum measurements. Our approach combines the addition of classical and quantum noise and is motivated by the noisy nature of near-term quantum devices. Moreover, we also investigate an alternative setting where we are provided with multiple copies of the input state. In this case, differential privacy can be ensured with little loss in accuracy combining concentration of measure and noise-adding mechanisms. En route, we prove the advanced joint convexity of the quantum hockey-stick divergence and we demonstrate how this result can be applied to quantum differential privacy. Finally, we complement our theoretical findings with an empirical estimation of the certified adversarial robustness ensured by differentially private measurements.

Differential Privacy Amplification in Quantum and Quantum-inspired Algorithms

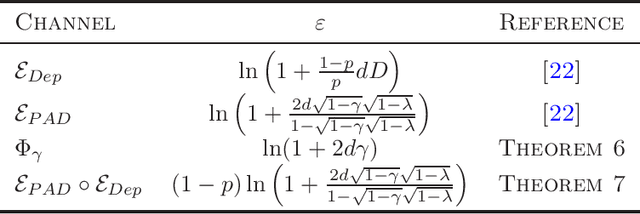
Differential privacy provides a theoretical framework for processing a dataset about $n$ users, in a way that the output reveals a minimal information about any single user. Such notion of privacy is usually ensured by noise-adding mechanisms and amplified by several processes, including subsampling, shuffling, iteration, mixing and diffusion. In this work, we provide privacy amplification bounds for quantum and quantum-inspired algorithms. In particular, we show for the first time, that algorithms running on quantum encoding of a classical dataset or the outcomes of quantum-inspired classical sampling, amplify differential privacy. Moreover, we prove that a quantum version of differential privacy is amplified by the composition of quantum channels, provided that they satisfy some mixing conditions.

Quantum Local Differential Privacy and Quantum Statistical Query Model

The problem of private learning has been extensively studied in classical computer science. Notably, a striking equivalence between local differentially private learning and statistical query learning has been shown. In addition, the statistical query model has been recently extended to quantum computation. In this work, we give a formal definition of quantum local differential privacy and we extend the aforementioned result to quantum computation.