Role of scrambling and noise in temporal information processing with quantum systems

Scrambling quantum systems have been demonstrated as effective substrates for temporal information processing. While their role in providing rich feature maps has been widely studied, a theoretical understanding of their performance in temporal tasks is still lacking. Here we consider a general quantum reservoir processing framework that captures a broad range of physical computing models with quantum systems. We examine the scalability and memory retention of the model with scrambling reservoirs modelled by high-order unitary designs in both noiseless and noisy settings. In the former regime, we show that measurement readouts become exponentially concentrated with increasing reservoir size, yet strikingly do not worsen with the reservoir iterations. Thus, while repeatedly reusing a small scrambling reservoir with quantum data might be viable, scaling up the problem size deteriorates generalization unless one can afford an exponential shot overhead. In contrast, the memory of early inputs and initial states decays exponentially in both reservoir size and reservoir iterations. In the noisy regime, we also prove exponential memory decays with iterations for local noisy channels. Proving these results required us to introduce new proof techniques for bounding concentration in temporal quantum learning models.

A unifying account of warm start guarantees for patches of quantum landscapes

Barren plateaus are fundamentally a statement about quantum loss landscapes on average but there can, and generally will, exist patches of barren plateau landscapes with substantial gradients. Previous work has studied certain classes of parameterized quantum circuits and found example regions where gradients vanish at worst polynomially in system size. Here we present a general bound that unifies all these previous cases and that can tackle physically-motivated ans\"atze that could not be analyzed previously. Concretely, we analytically prove a lower-bound on the variance of the loss that can be used to show that in a non-exponentially narrow region around a point with curvature the loss variance cannot decay exponentially fast. This result is complemented by numerics and an upper-bound that suggest that any loss function with a barren plateau will have exponentially vanishing gradients in any constant radius subregion. Our work thus suggests that while there are hopes to be able to warm-start variational quantum algorithms, any initialization strategy that cannot get increasingly close to the region of attraction with increasing problem size is likely inadequate.

Efficient quantum-enhanced classical simulation for patches of quantum landscapes

Understanding the capabilities of classical simulation methods is key to identifying where quantum computers are advantageous. Not only does this ensure that quantum computers are used only where necessary, but also one can potentially identify subroutines that can be offloaded onto a classical device. In this work, we show that it is always possible to generate a classical surrogate of a sub-region (dubbed a "patch") of an expectation landscape produced by a parameterized quantum circuit. That is, we provide a quantum-enhanced classical algorithm which, after simple measurements on a quantum device, allows one to classically simulate approximate expectation values of a subregion of a landscape. We provide time and sample complexity guarantees for a range of families of circuits of interest, and further numerically demonstrate our simulation algorithms on an exactly verifiable simulation of a Hamiltonian variational ansatz and long-time dynamics simulation on a 127-qubit heavy-hex topology.

A Review of Barren Plateaus in Variational Quantum Computing

Variational quantum computing offers a flexible computational paradigm with applications in diverse areas. However, a key obstacle to realizing their potential is the Barren Plateau (BP) phenomenon. When a model exhibits a BP, its parameter optimization landscape becomes exponentially flat and featureless as the problem size increases. Importantly, all the moving pieces of an algorithm -- choices of ansatz, initial state, observable, loss function and hardware noise -- can lead to BPs when ill-suited. Due to the significant impact of BPs on trainability, researchers have dedicated considerable effort to develop theoretical and heuristic methods to understand and mitigate their effects. As a result, the study of BPs has become a thriving area of research, influencing and cross-fertilizing other fields such as quantum optimal control, tensor networks, and learning theory. This article provides a comprehensive review of the current understanding of the BP phenomenon.

Variational quantum simulation: a case study for understanding warm starts

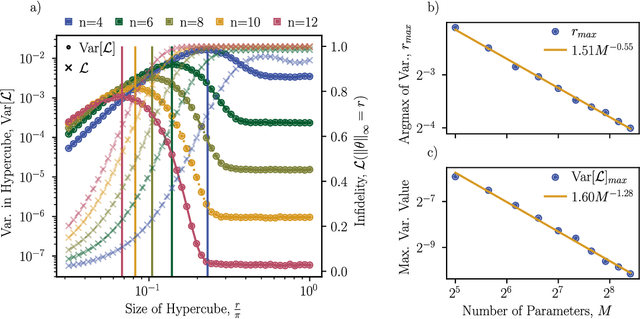
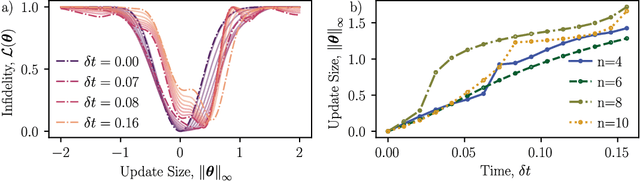
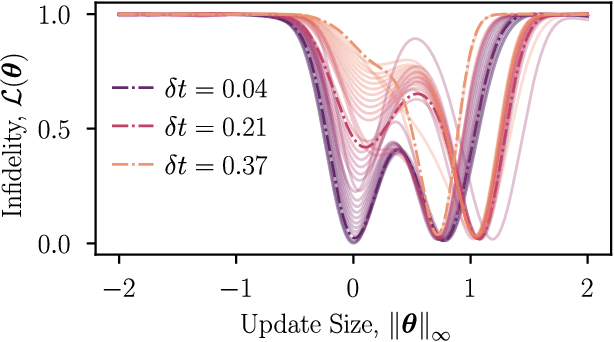
The barren plateau phenomenon, characterized by loss gradients that vanish exponentially with system size, poses a challenge to scaling variational quantum algorithms. Here we explore the potential of warm starts, whereby one initializes closer to a solution in the hope of enjoying larger loss variances. Focusing on an iterative variational method for learning shorter-depth circuits for quantum real and imaginary time evolution we conduct a case study to elucidate the potential and limitations of warm starts. We start by proving that the iterative variational algorithm will exhibit substantial (at worst vanishing polynomially in system size) gradients in a small region around the initializations at each time-step. Convexity guarantees for these regions are then established, suggesting trainability for polynomial size time-steps. However, our study highlights scenarios where a good minimum shifts outside the region with trainability guarantees. Our analysis leaves open the question whether such minima jumps necessitate optimization across barren plateau landscapes or whether there exist gradient flows, i.e., fertile valleys away from the plateau with substantial gradients, that allow for training.

On fundamental aspects of quantum extreme learning machines

Quantum Extreme Learning Machines (QELMs) have emerged as a promising framework for quantum machine learning. Their appeal lies in the rich feature map induced by the dynamics of a quantum substrate - the quantum reservoir - and the efficient post-measurement training via linear regression. Here we study the expressivity of QELMs by decomposing the prediction of QELMs into a Fourier series. We show that the achievable Fourier frequencies are determined by the data encoding scheme, while Fourier coefficients depend on both the reservoir and the measurement. Notably, the expressivity of QELMs is fundamentally limited by the number of Fourier frequencies and the number of observables, while the complexity of the prediction hinges on the reservoir. As a cautionary note on scalability, we identify four sources that can lead to the exponential concentration of the observables as the system size grows (randomness, hardware noise, entanglement, and global measurements) and show how this can turn QELMs into useless input-agnostic oracles. Our analysis elucidates the potential and fundamental limitations of QELMs, and lays the groundwork for systematically exploring quantum reservoir systems for other machine learning tasks.

Does provable absence of barren plateaus imply classical simulability? Or, why we need to rethink variational quantum computing

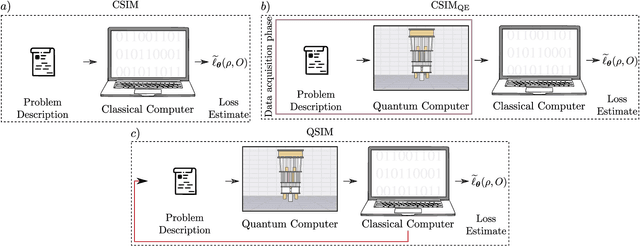
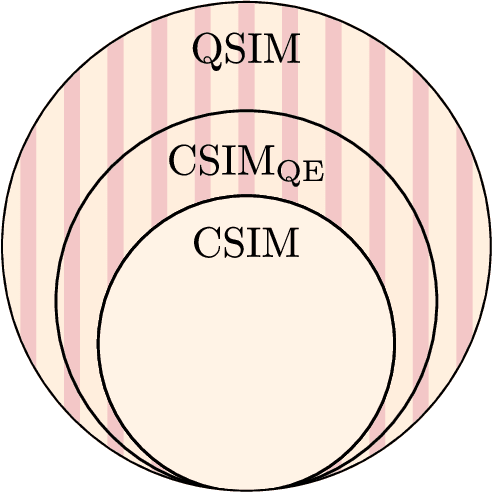
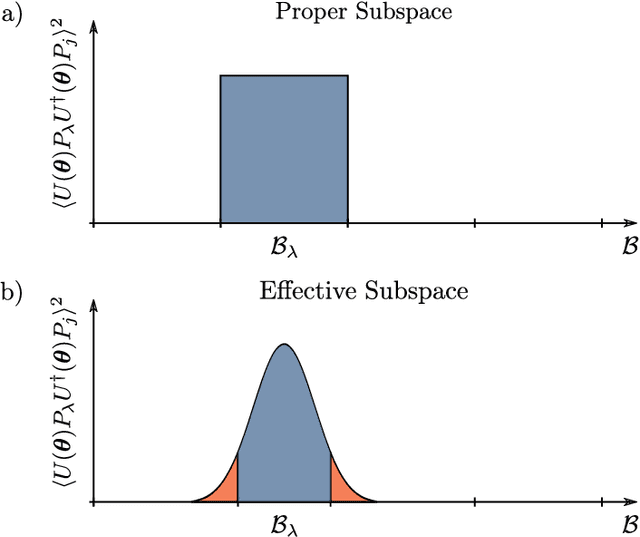
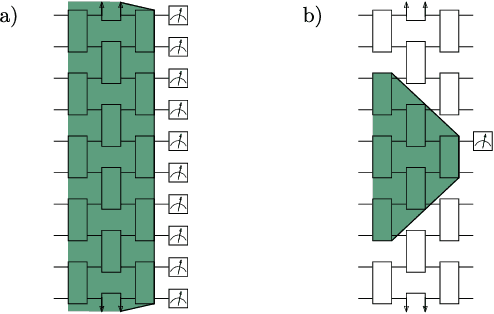
A large amount of effort has recently been put into understanding the barren plateau phenomenon. In this perspective article, we face the increasingly loud elephant in the room and ask a question that has been hinted at by many but not explicitly addressed: Can the structure that allows one to avoid barren plateaus also be leveraged to efficiently simulate the loss classically? We present strong evidence that commonly used models with provable absence of barren plateaus are also classically simulable, provided that one can collect some classical data from quantum devices during an initial data acquisition phase. This follows from the observation that barren plateaus result from a curse of dimensionality, and that current approaches for solving them end up encoding the problem into some small, classically simulable, subspaces. This sheds serious doubt on the non-classicality of the information processing capabilities of parametrized quantum circuits for barren plateau-free landscapes and on the possibility of superpolynomial advantages from running them on quantum hardware. We end by discussing caveats in our arguments, the role of smart initializations, and by highlighting new opportunities that our perspective raises.

A Unified Framework for Trace-induced Quantum Kernels

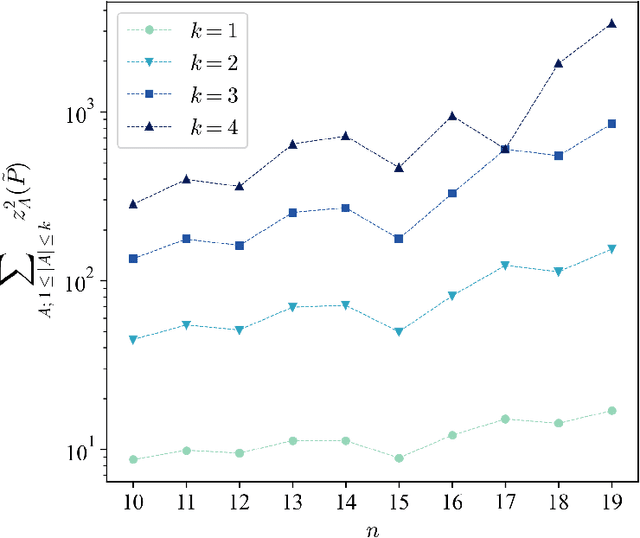
Quantum kernel methods are promising candidates for achieving a practical quantum advantage for certain machine learning tasks. Similar to classical machine learning, an exact form of a quantum kernel is expected to have a great impact on the model performance. In this work we combine all trace-induced quantum kernels, including the commonly-used global fidelity and local projected quantum kernels, into a common framework. We show how generalized trace-induced quantum kernels can be constructed as combinations of the fundamental building blocks we coin "Lego" kernels, which impose an inductive bias on the resulting quantum models. We relate the expressive power and generalization ability to the number of non-zero weight Lego kernels and propose a systematic approach to increase the complexity of a quantum kernel model, leading to a new form of the local projected kernels that require fewer quantum resources in terms of the number of quantum gates and measurement shots. We show numerically that models based on local projected kernels can achieve comparable performance to the global fidelity quantum kernel. Our work unifies existing quantum kernels and provides a systematic framework to compare their properties.

Trainability barriers and opportunities in quantum generative modeling

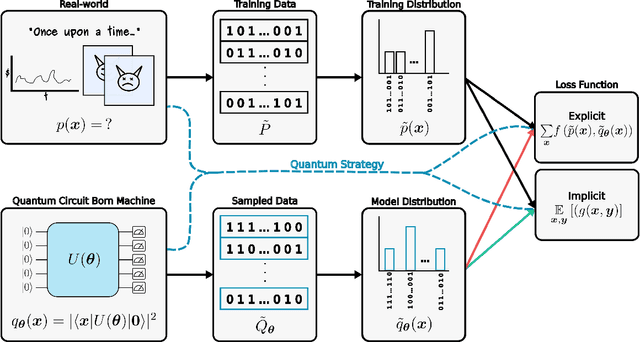
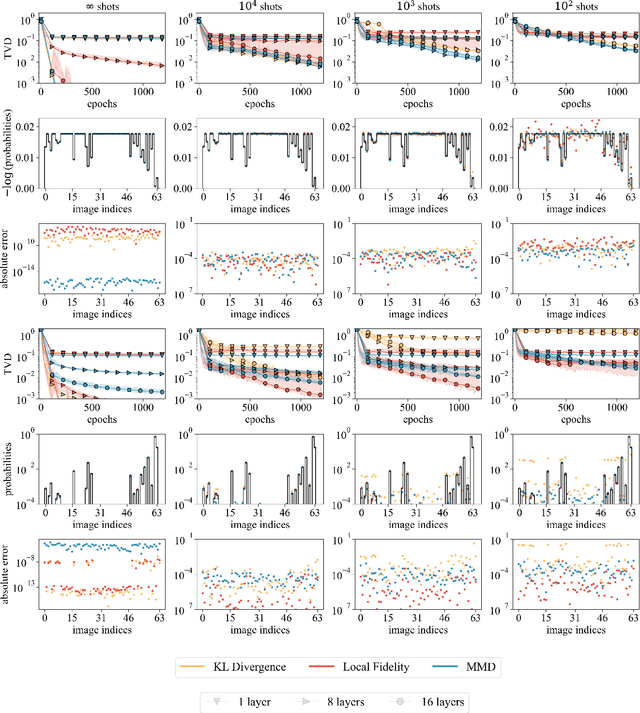
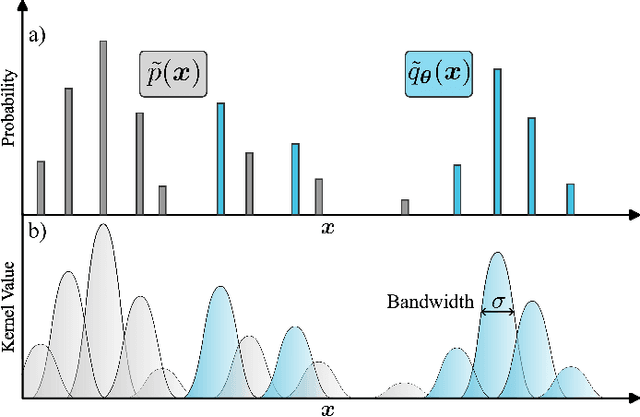
Quantum generative models, in providing inherently efficient sampling strategies, show promise for achieving a near-term advantage on quantum hardware. Nonetheless, important questions remain regarding their scalability. In this work, we investigate the barriers to the trainability of quantum generative models posed by barren plateaus and exponential loss concentration. We explore the interplay between explicit and implicit models and losses, and show that using implicit generative models (such as quantum circuit-based models) with explicit losses (such as the KL divergence) leads to a new flavour of barren plateau. In contrast, the Maximum Mean Discrepancy (MMD), which is a popular example of an implicit loss, can be viewed as the expectation value of an observable that is either low-bodied and trainable, or global and untrainable depending on the choice of kernel. However, in parallel, we highlight that the low-bodied losses required for trainability cannot in general distinguish high-order correlations, leading to a fundamental tension between exponential concentration and the emergence of spurious minima. We further propose a new local quantum fidelity-type loss which, by leveraging quantum circuits to estimate the quality of the encoded distribution, is both faithful and enjoys trainability guarantees. Finally, we compare the performance of different loss functions for modelling real-world data from the High-Energy-Physics domain and confirm the trends predicted by our theoretical results.

Exponential concentration and untrainability in quantum kernel methods

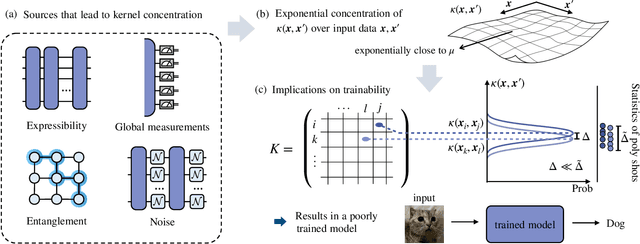
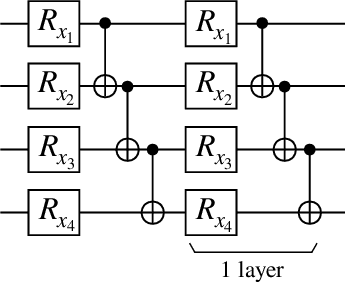
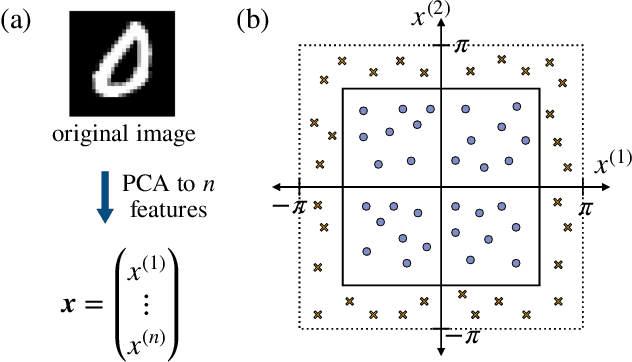
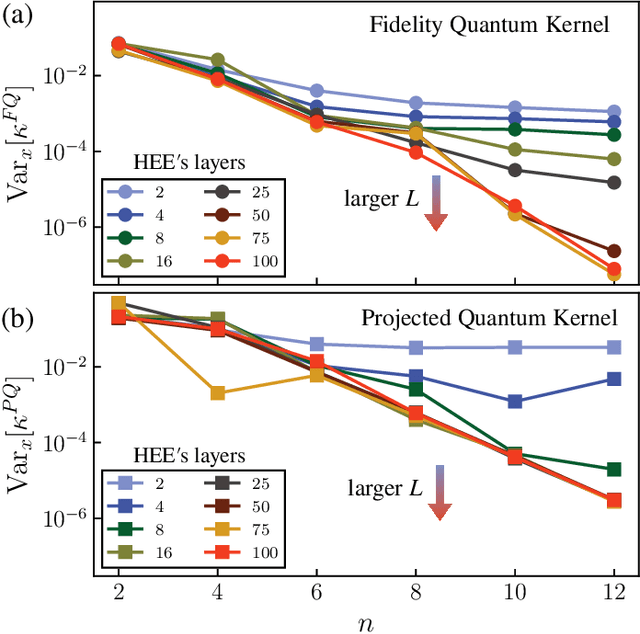
Kernel methods in Quantum Machine Learning (QML) have recently gained significant attention as a potential candidate for achieving a quantum advantage in data analysis. Among other attractive properties, when training a kernel-based model one is guaranteed to find the optimal model's parameters due to the convexity of the training landscape. However, this is based on the assumption that the quantum kernel can be efficiently obtained from a quantum hardware. In this work we study the trainability of quantum kernels from the perspective of the resources needed to accurately estimate kernel values. We show that, under certain conditions, values of quantum kernels over different input data can be exponentially concentrated (in the number of qubits) towards some fixed value, leading to an exponential scaling of the number of measurements required for successful training. We identify four sources that can lead to concentration including: the expressibility of data embedding, global measurements, entanglement and noise. For each source, an associated concentration bound of quantum kernels is analytically derived. Lastly, we show that when dealing with classical data, training a parametrized data embedding with a kernel alignment method is also susceptible to exponential concentration. Our results are verified through numerical simulations for several QML tasks. Altogether, we provide guidelines indicating that certain features should be avoided to ensure the efficient evaluation and the trainability of quantum kernel methods.