Quantum Convolutional Neural Networks are (Effectively) Classically Simulable

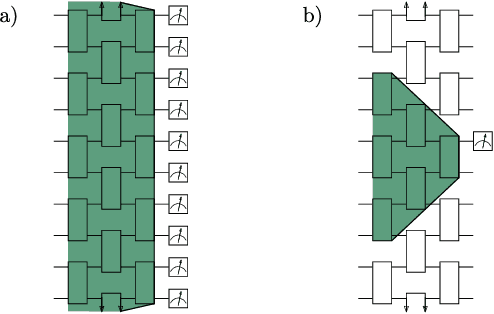
Quantum Convolutional Neural Networks (QCNNs) are widely regarded as a promising model for Quantum Machine Learning (QML). In this work we tie their heuristic success to two facts. First, that when randomly initialized, they can only operate on the information encoded in low-bodyness measurements of their input states. And second, that they are commonly benchmarked on "locally-easy'' datasets whose states are precisely classifiable by the information encoded in these low-bodyness observables subspace. We further show that the QCNN's action on this subspace can be efficiently classically simulated by a classical algorithm equipped with Pauli shadows on the dataset. Indeed, we present a shadow-based simulation of QCNNs on up-to $1024$ qubits for phases of matter classification. Our results can then be understood as highlighting a deeper symptom of QML: Models could only be showing heuristic success because they are benchmarked on simple problems, for which their action can be classically simulated. This insight points to the fact that non-trivial datasets are a truly necessary ingredient for moving forward with QML. To finish, we discuss how our results can be extrapolated to classically simulate other architectures.

Does provable absence of barren plateaus imply classical simulability? Or, why we need to rethink variational quantum computing

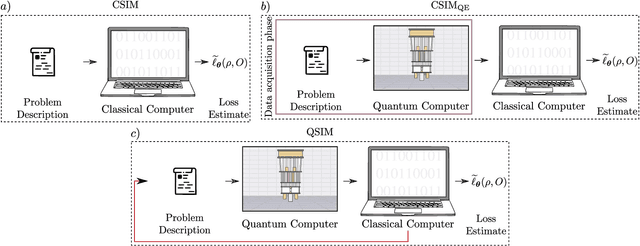
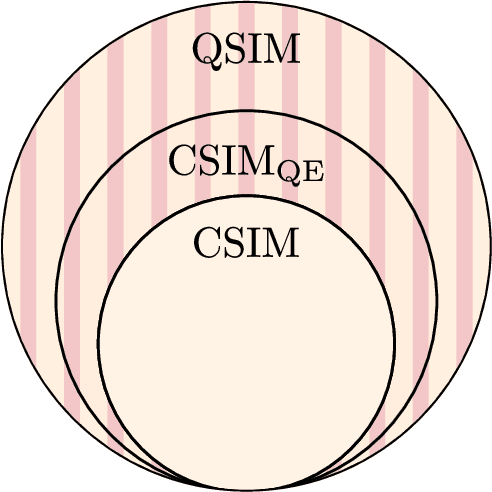
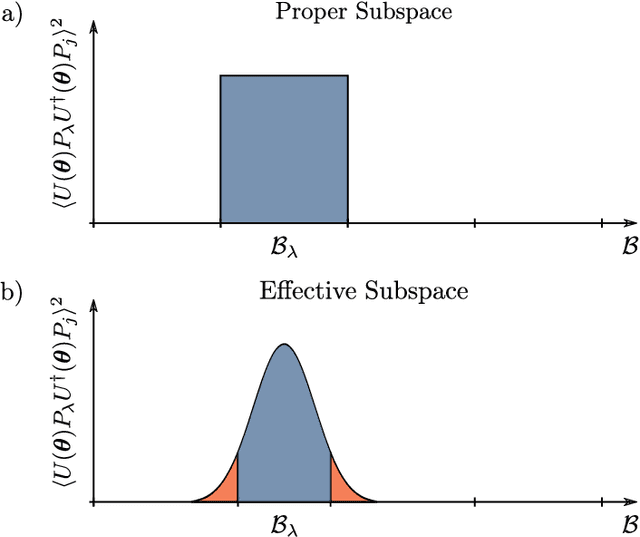
A large amount of effort has recently been put into understanding the barren plateau phenomenon. In this perspective article, we face the increasingly loud elephant in the room and ask a question that has been hinted at by many but not explicitly addressed: Can the structure that allows one to avoid barren plateaus also be leveraged to efficiently simulate the loss classically? We present strong evidence that commonly used models with provable absence of barren plateaus are also classically simulable, provided that one can collect some classical data from quantum devices during an initial data acquisition phase. This follows from the observation that barren plateaus result from a curse of dimensionality, and that current approaches for solving them end up encoding the problem into some small, classically simulable, subspaces. This sheds serious doubt on the non-classicality of the information processing capabilities of parametrized quantum circuits for barren plateau-free landscapes and on the possibility of superpolynomial advantages from running them on quantum hardware. We end by discussing caveats in our arguments, the role of smart initializations, and by highlighting new opportunities that our perspective raises.

Hacking Cryptographic Protocols with Advanced Variational Quantum Attacks

Here we introduce an improved approach to Variational Quantum Attack Algorithms (VQAA) on crytographic protocols. Our methods provide robust quantum attacks to well-known cryptographic algorithms, more efficiently and with remarkably fewer qubits than previous approaches. We implement simulations of our attacks for symmetric-key protocols such as S-DES, S-AES and Blowfish. For instance, we show how our attack allows a classical simulation of a small 8-qubit quantum computer to find the secret key of one 32-bit Blowfish instance with 24 times fewer number of iterations than a brute-force attack. Our work also shows improvements in attack success rates for lightweight ciphers such as S-DES and S-AES. Further applications beyond symmetric-key cryptography are also discussed, including asymmetric-key protocols and hash functions. In addition, we also comment on potential future improvements of our methods. Our results bring one step closer assessing the vulnerability of large-size classical cryptographic protocols with Noisy Intermediate-Scale Quantum (NISQ) devices, and set the stage for future research in quantum cybersecurity.

Improving Gradient Methods via Coordinate Transformations: Applications to Quantum Machine Learning

Machine learning algorithms, both in their classical and quantum versions, heavily rely on optimization algorithms based on gradients, such as gradient descent and alike. The overall performance is dependent on the appearance of local minima and barren plateaus, which slow-down calculations and lead to non-optimal solutions. In practice, this results in dramatic computational and energy costs for AI applications. In this paper we introduce a generic strategy to accelerate and improve the overall performance of such methods, allowing to alleviate the effect of barren plateaus and local minima. Our method is based on coordinate transformations, somehow similar to variational rotations, adding extra directions in parameter space that depend on the cost function itself, and which allow to explore the configuration landscape more efficiently. The validity of our method is benchmarked by boosting a number of quantum machine learning algorithms, getting a very significant improvement in their performance.

Variational Quantum and Quantum-Inspired Clustering

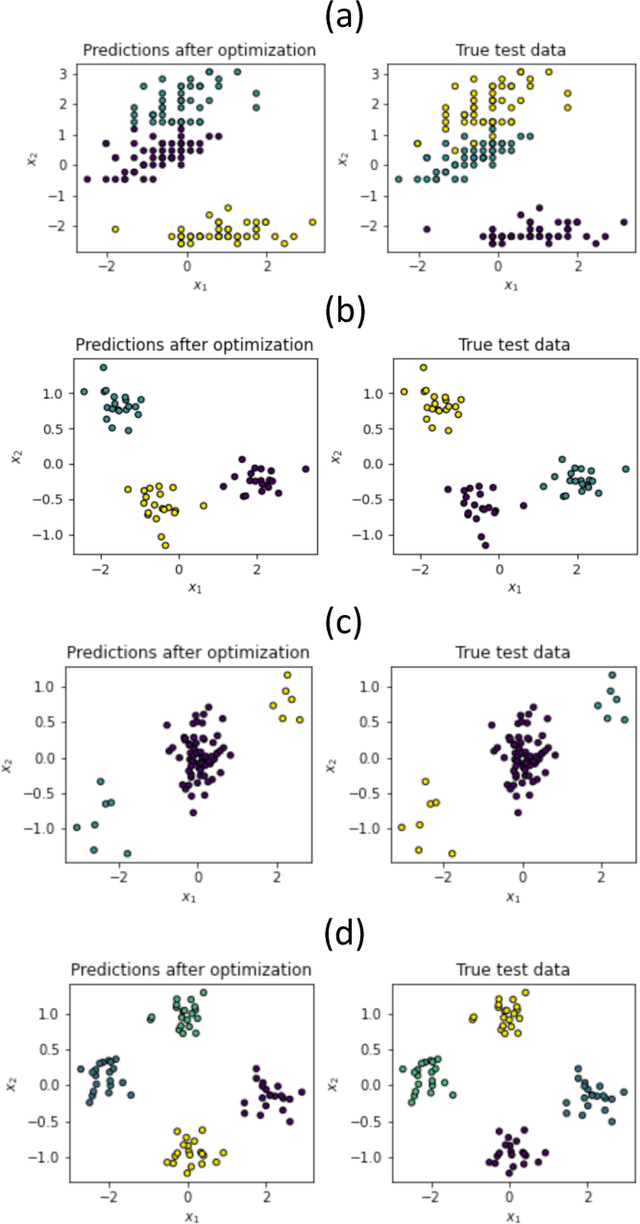
Here we present a quantum algorithm for clustering data based on a variational quantum circuit. The algorithm allows to classify data into many clusters, and can easily be implemented in few-qubit Noisy Intermediate-Scale Quantum (NISQ) devices. The idea of the algorithm relies on reducing the clustering problem to an optimization, and then solving it via a Variational Quantum Eigensolver (VQE) combined with non-orthogonal qubit states. In practice, the method uses maximally-orthogonal states of the target Hilbert space instead of the usual computational basis, allowing for a large number of clusters to be considered even with few qubits. We benchmark the algorithm with numerical simulations using real datasets, showing excellent performance even with one single qubit. Moreover, a tensor network simulation of the algorithm implements, by construction, a quantum-inspired clustering algorithm that can run on current classical hardware.