Does provable absence of barren plateaus imply classical simulability? Or, why we need to rethink variational quantum computing

A large amount of effort has recently been put into understanding the barren plateau phenomenon. In this perspective article, we face the increasingly loud elephant in the room and ask a question that has been hinted at by many but not explicitly addressed: Can the structure that allows one to avoid barren plateaus also be leveraged to efficiently simulate the loss classically? We present strong evidence that commonly used models with provable absence of barren plateaus are also classically simulable, provided that one can collect some classical data from quantum devices during an initial data acquisition phase. This follows from the observation that barren plateaus result from a curse of dimensionality, and that current approaches for solving them end up encoding the problem into some small, classically simulable, subspaces. This sheds serious doubt on the non-classicality of the information processing capabilities of parametrized quantum circuits for barren plateau-free landscapes and on the possibility of superpolynomial advantages from running them on quantum hardware. We end by discussing caveats in our arguments, the role of smart initializations, and by highlighting new opportunities that our perspective raises.

Optimizing parametrized quantum circuits via noise-induced breaking of symmetries

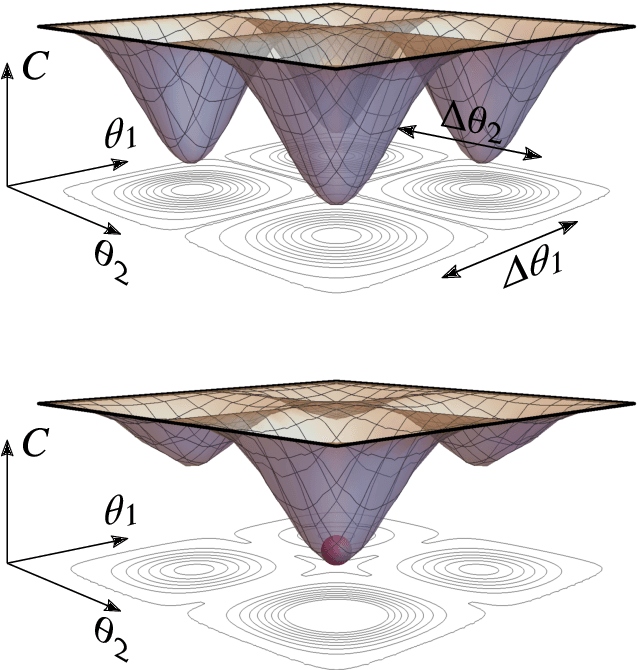
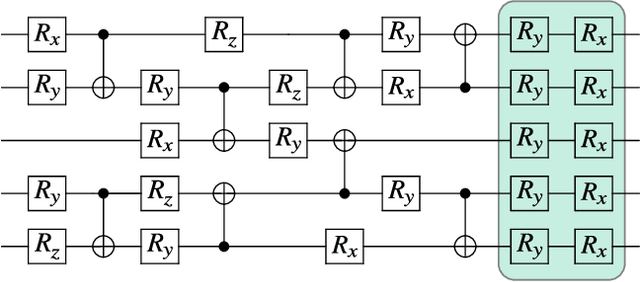
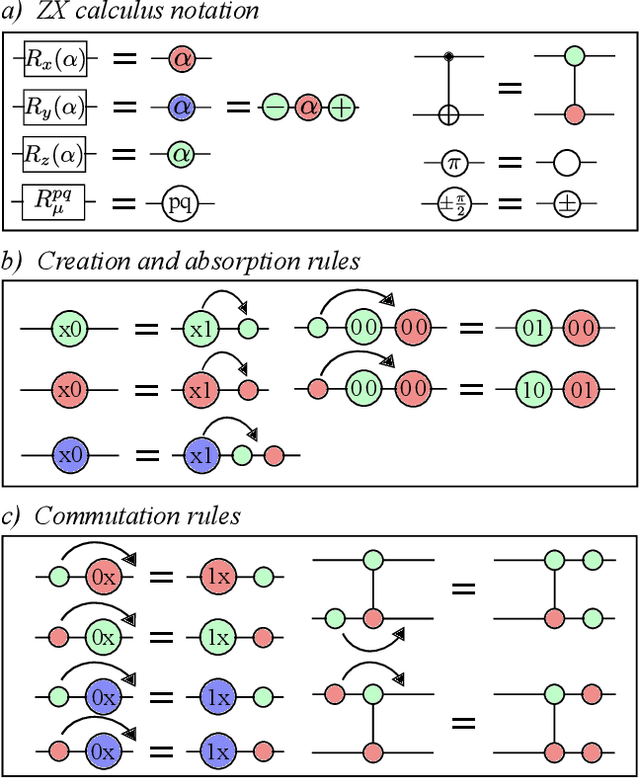
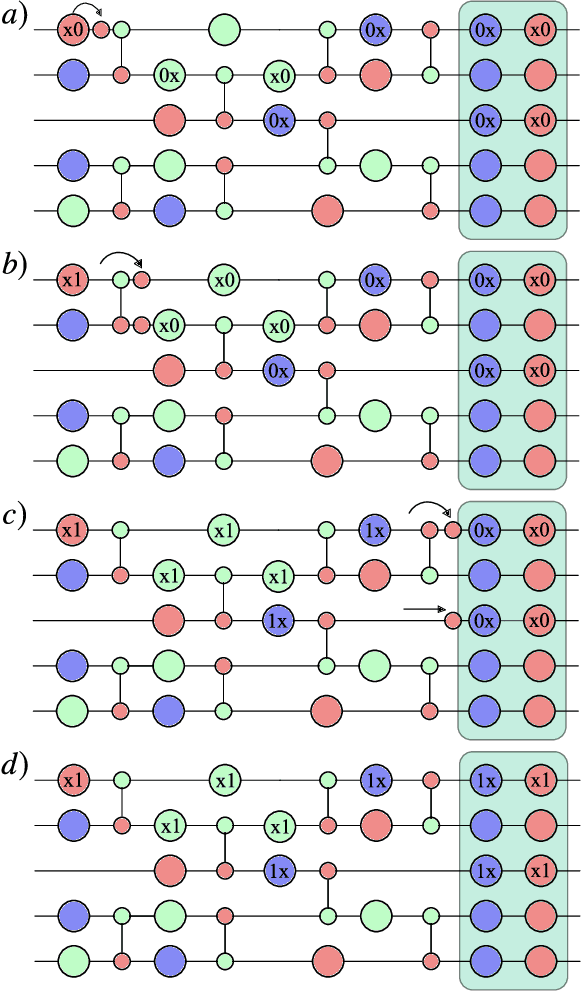
Very little is known about the cost landscape for parametrized Quantum Circuits (PQCs). Nevertheless, PQCs are employed in Quantum Neural Networks and Variational Quantum Algorithms, which may allow for near-term quantum advantage. Such applications require good optimizers to train PQCs. Recent works have focused on quantum-aware optimizers specifically tailored for PQCs. However, ignorance of the cost landscape could hinder progress towards such optimizers. In this work, we analytically prove two results for PQCs: (1) We find an exponentially large symmetry in PQCs, yielding an exponentially large degeneracy of the minima in the cost landscape. (2) We show that noise (specifically non-unital noise) can break these symmetries and lift the degeneracy of minima, making many of them local minima instead of global minima. Based on these results, we introduce an optimization method called Symmetry-based Minima Hopping (SYMH), which exploits the underlying symmetries in PQCs to hop between local minima in the cost landscape. The versatility of SYMH allows it to be combined with local optimizers (e.g., gradient descent) with minimal overhead. Our numerical simulations show that SYMH improves the overall optimizer performance.

Noise-Induced Barren Plateaus in Variational Quantum Algorithms

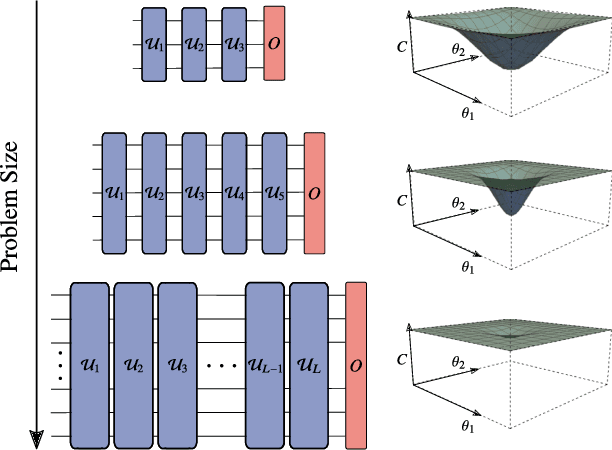
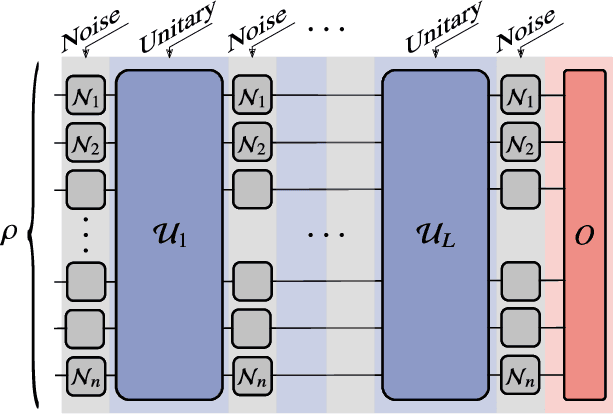
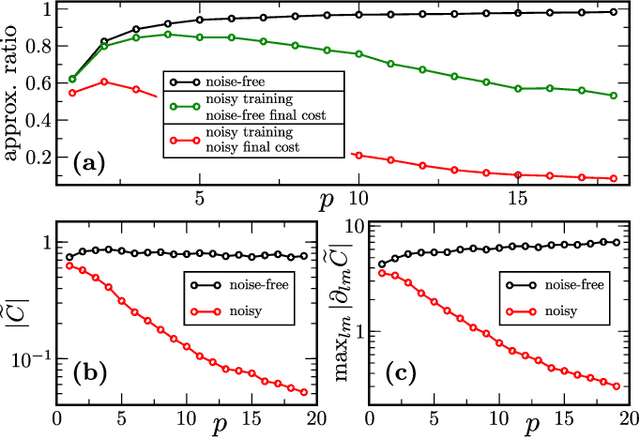
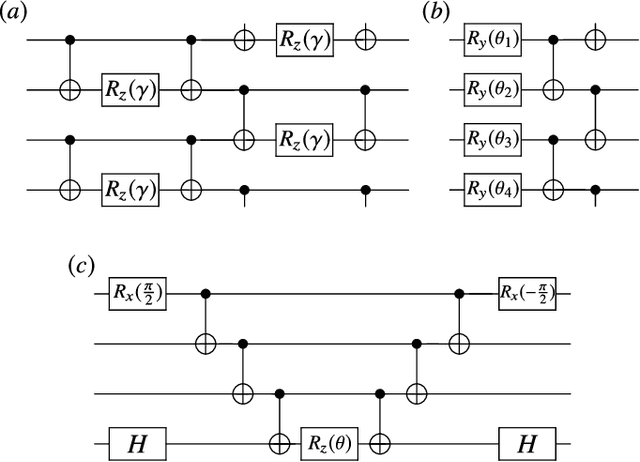
Variational Quantum Algorithms (VQAs) may be a path to quantum advantage on Noisy Intermediate-Scale Quantum (NISQ) computers. A natural question is whether the noise on NISQ devices places any fundamental limitations on the performance of VQAs. In this work, we rigorously prove a serious limitation for noisy VQAs, in that the noise causes the training landscape to have a barren plateau (i.e., vanishing gradient). Specifically, for the local Pauli noise considered, we prove that the gradient vanishes exponentially in the number of layers $L$. This implies exponential decay in the number of qubits $n$ when $L$ scales as $\operatorname{poly}(n)$, for sufficiently large coefficients in the polynomial. These noise-induced barren plateaus (NIBPs) are conceptually different from noise-free barren plateaus, which are linked to random parameter initialization. Our result is formulated for an abstract ansatz that includes as special cases the Quantum Alternating Operator Ansatz (QAOA) and the Unitary Coupled Cluster Ansatz, among others. In the case of the QAOA, we implement numerical heuristics that confirm the NIBP phenomenon for a realistic hardware noise model.