Quantum Convolutional Neural Networks are (Effectively) Classically Simulable

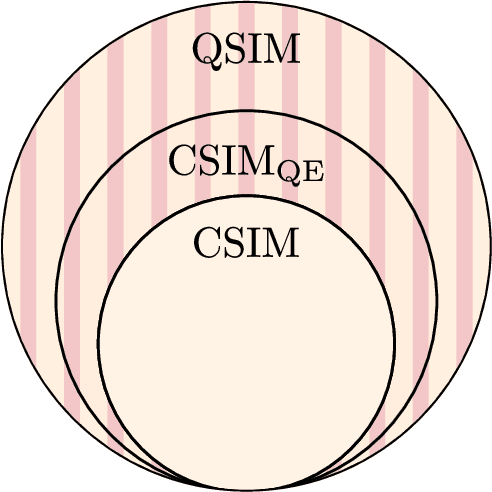
Quantum Convolutional Neural Networks (QCNNs) are widely regarded as a promising model for Quantum Machine Learning (QML). In this work we tie their heuristic success to two facts. First, that when randomly initialized, they can only operate on the information encoded in low-bodyness measurements of their input states. And second, that they are commonly benchmarked on "locally-easy'' datasets whose states are precisely classifiable by the information encoded in these low-bodyness observables subspace. We further show that the QCNN's action on this subspace can be efficiently classically simulated by a classical algorithm equipped with Pauli shadows on the dataset. Indeed, we present a shadow-based simulation of QCNNs on up-to $1024$ qubits for phases of matter classification. Our results can then be understood as highlighting a deeper symptom of QML: Models could only be showing heuristic success because they are benchmarked on simple problems, for which their action can be classically simulated. This insight points to the fact that non-trivial datasets are a truly necessary ingredient for moving forward with QML. To finish, we discuss how our results can be extrapolated to classically simulate other architectures.

Architectures and random properties of symplectic quantum circuits

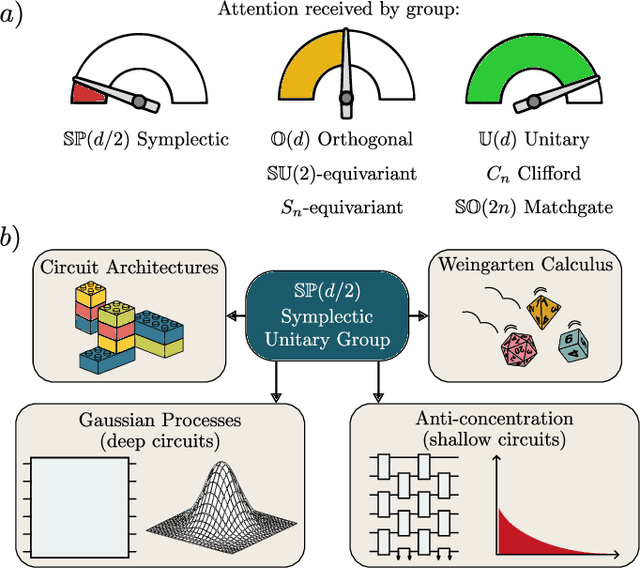
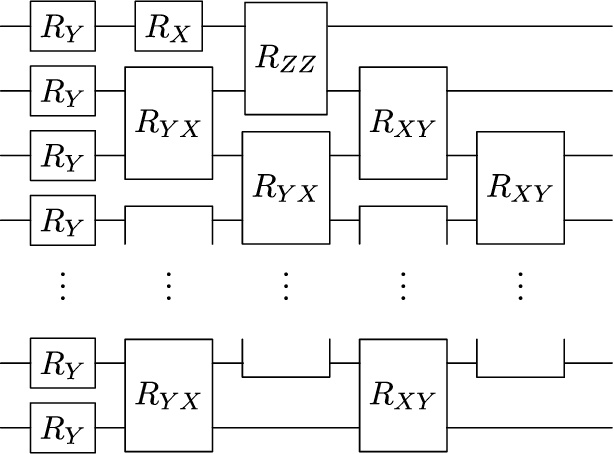
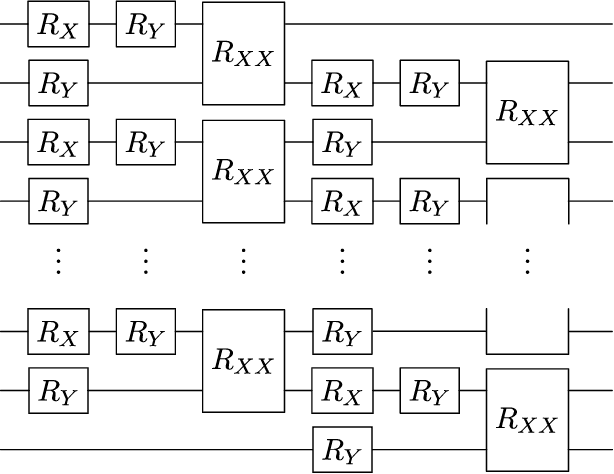
Parametrized and random unitary (or orthogonal) $n$-qubit circuits play a central role in quantum information. As such, one could naturally assume that circuits implementing symplectic transformation would attract similar attention. However, this is not the case, as $\mathbb{SP}(d/2)$ -- the group of $d\times d$ unitary symplectic matrices -- has thus far been overlooked. In this work, we aim at starting to right this wrong. We begin by presenting a universal set of generators $\mathcal{G}$ for the symplectic algebra $i\mathfrak{sp}(d/2)$, consisting of one- and two-qubit Pauli operators acting on neighboring sites in a one-dimensional lattice. Here, we uncover two critical differences between such set, and equivalent ones for unitary and orthogonal circuits. Namely, we find that the operators in $\mathcal{G}$ cannot generate arbitrary local symplectic unitaries and that they are not translationally invariant. We then review the Schur-Weyl duality between the symplectic group and the Brauer algebra, and use tools from Weingarten calculus to prove that Pauli measurements at the output of Haar random symplectic circuits can converge to Gaussian processes. As a by-product, such analysis provides us with concentration bounds for Pauli measurements in circuits that form $t$-designs over $\mathbb{SP}(d/2)$. To finish, we present tensor-network tools to analyze shallow random symplectic circuits, and we use these to numerically show that computational-basis measurements anti-concentrate at logarithmic depth.

Does provable absence of barren plateaus imply classical simulability? Or, why we need to rethink variational quantum computing

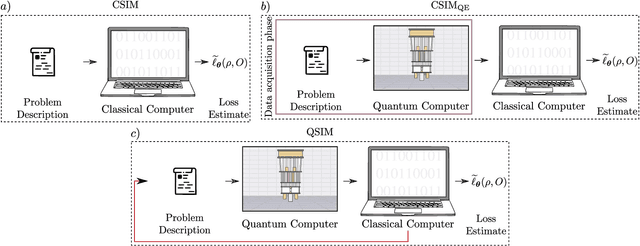
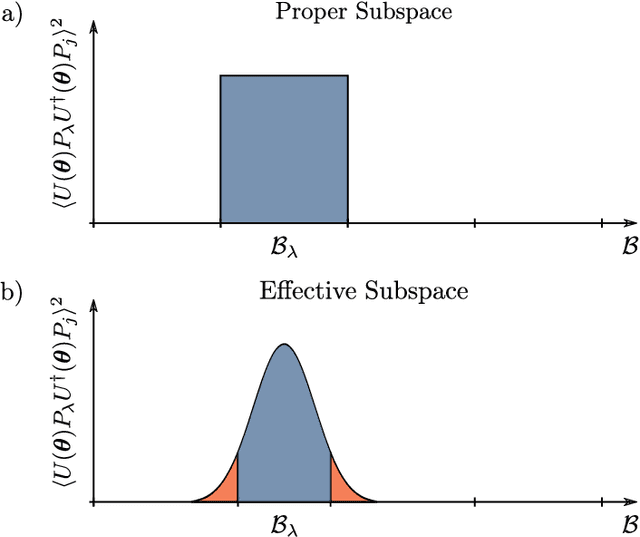
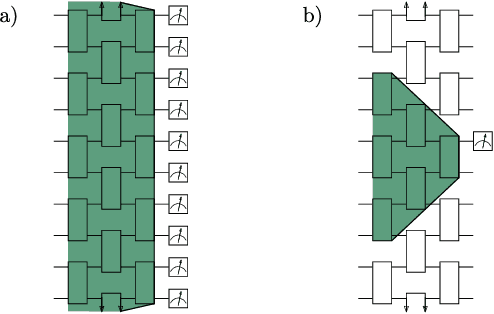
A large amount of effort has recently been put into understanding the barren plateau phenomenon. In this perspective article, we face the increasingly loud elephant in the room and ask a question that has been hinted at by many but not explicitly addressed: Can the structure that allows one to avoid barren plateaus also be leveraged to efficiently simulate the loss classically? We present strong evidence that commonly used models with provable absence of barren plateaus are also classically simulable, provided that one can collect some classical data from quantum devices during an initial data acquisition phase. This follows from the observation that barren plateaus result from a curse of dimensionality, and that current approaches for solving them end up encoding the problem into some small, classically simulable, subspaces. This sheds serious doubt on the non-classicality of the information processing capabilities of parametrized quantum circuits for barren plateau-free landscapes and on the possibility of superpolynomial advantages from running them on quantum hardware. We end by discussing caveats in our arguments, the role of smart initializations, and by highlighting new opportunities that our perspective raises.

Theory for Equivariant Quantum Neural Networks

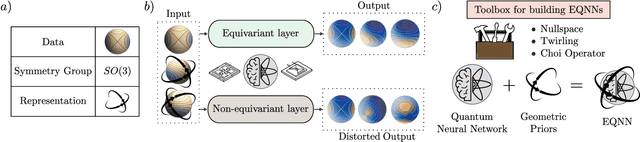
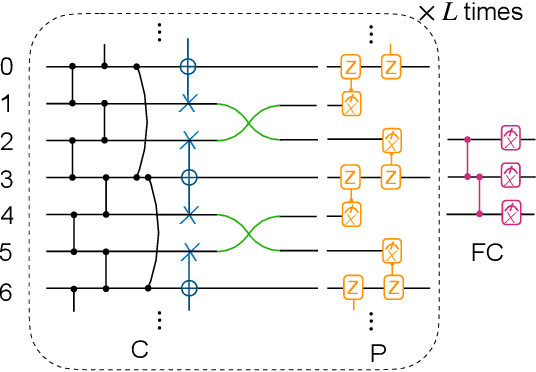
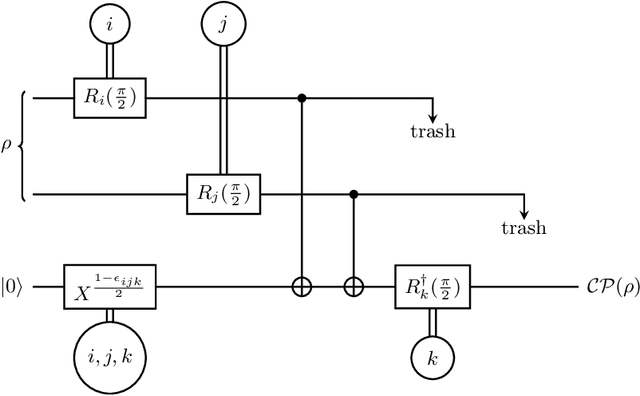
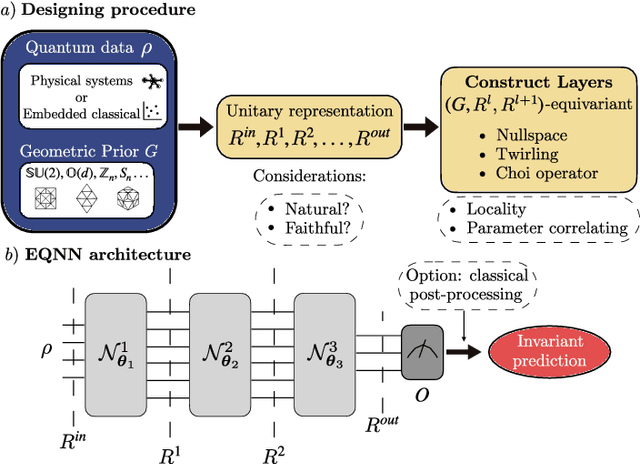
Most currently used quantum neural network architectures have little-to-no inductive biases, leading to trainability and generalization issues. Inspired by a similar problem, recent breakthroughs in classical machine learning address this crux by creating models encoding the symmetries of the learning task. This is materialized through the usage of equivariant neural networks whose action commutes with that of the symmetry. In this work, we import these ideas to the quantum realm by presenting a general theoretical framework to understand, classify, design and implement equivariant quantum neural networks. As a special implementation, we show how standard quantum convolutional neural networks (QCNN) can be generalized to group-equivariant QCNNs where both the convolutional and pooling layers are equivariant under the relevant symmetry group. Our framework can be readily applied to virtually all areas of quantum machine learning, and provides hope to alleviate central challenges such as barren plateaus, poor local minima, and sample complexity.

Representation Theory for Geometric Quantum Machine Learning

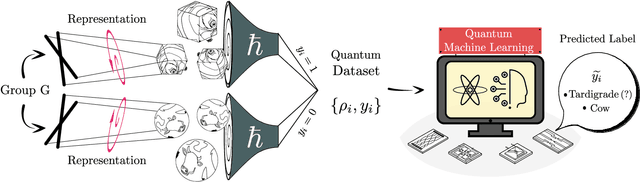
Recent advances in classical machine learning have shown that creating models with inductive biases encoding the symmetries of a problem can greatly improve performance. Importation of these ideas, combined with an existing rich body of work at the nexus of quantum theory and symmetry, has given rise to the field of Geometric Quantum Machine Learning (GQML). Following the success of its classical counterpart, it is reasonable to expect that GQML will play a crucial role in developing problem-specific and quantum-aware models capable of achieving a computational advantage. Despite the simplicity of the main idea of GQML -- create architectures respecting the symmetries of the data -- its practical implementation requires a significant amount of knowledge of group representation theory. We present an introduction to representation theory tools from the optics of quantum learning, driven by key examples involving discrete and continuous groups. These examples are sewn together by an exposition outlining the formal capture of GQML symmetries via "label invariance under the action of a group representation", a brief (but rigorous) tour through finite and compact Lie group representation theory, a reexamination of ubiquitous tools like Haar integration and twirling, and an overview of some successful strategies for detecting symmetries.