On the Role of Entanglement and Statistics in Learning

In this work we make progress in understanding the relationship between learning models with access to entangled, separable and statistical measurements in the quantum statistical query (QSQ) model. To this end, we show the following results. $\textbf{Entangled versus separable measurements.}$ The goal here is to learn an unknown $f$ from the concept class $C\subseteq \{f:\{0,1\}^n\rightarrow [k]\}$ given copies of $\frac{1}{\sqrt{2^n}}\sum_x \vert x,f(x)\rangle$. We show that, if $T$ copies suffice to learn $f$ using entangled measurements, then $O(nT^2)$ copies suffice to learn $f$ using just separable measurements. $\textbf{Entangled versus statistical measurements}$ The goal here is to learn a function $f \in C$ given access to separable measurements and statistical measurements. We exhibit a class $C$ that gives an exponential separation between QSQ learning and quantum learning with entangled measurements (even in the presence of noise). This proves the "quantum analogue" of the seminal result of Blum et al. [BKW'03]. that separates classical SQ and PAC learning with classification noise. $\textbf{QSQ lower bounds for learning states.}$ We introduce a quantum statistical query dimension (QSD), which we use to give lower bounds on the QSQ learning. With this we prove superpolynomial QSQ lower bounds for testing purity, shadow tomography, Abelian hidden subgroup problem, degree-$2$ functions, planted bi-clique states and output states of Clifford circuits of depth $\textsf{polylog}(n)$. $\textbf{Further applications.}$ We give and $\textit{unconditional}$ separation between weak and strong error mitigation and prove lower bounds for learning distributions in the QSQ model. Prior works by Quek et al. [QFK+'22], Hinsche et al. [HIN+'22], and Nietner et al. [NIS+'23] proved the analogous results $\textit{assuming}$ diagonal measurements and our work removes this assumption.

Theoretical Guarantees for Permutation-Equivariant Quantum Neural Networks

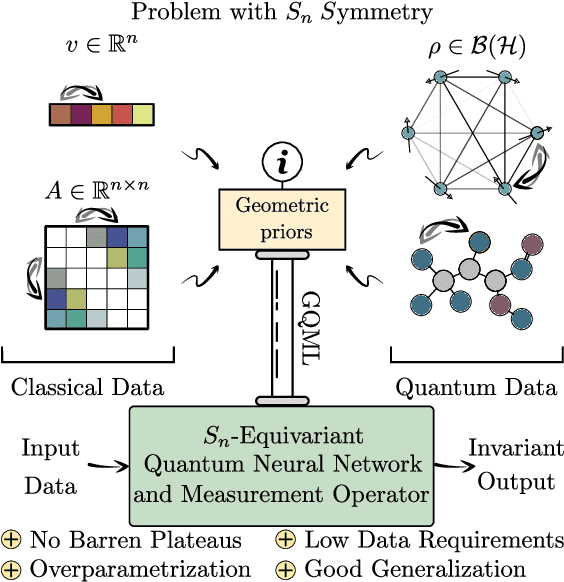
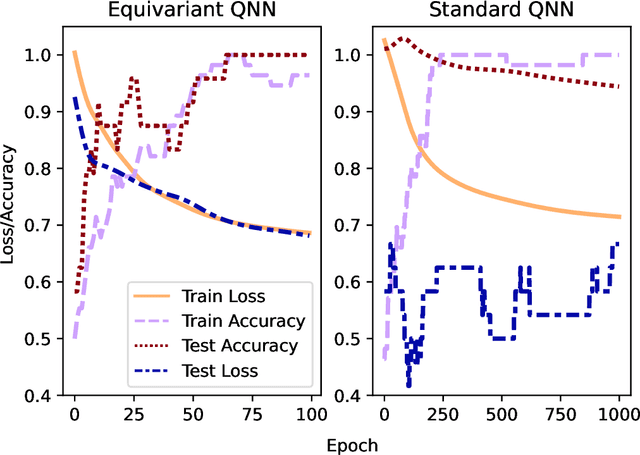
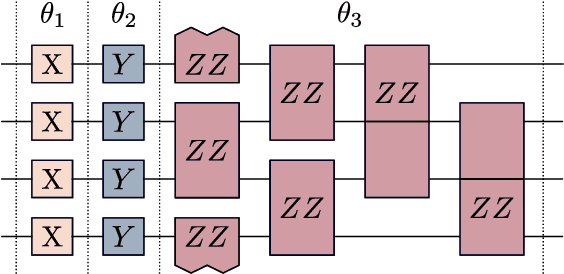
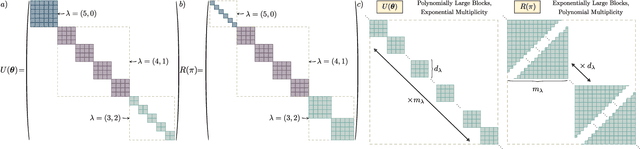
Despite the great promise of quantum machine learning models, there are several challenges one must overcome before unlocking their full potential. For instance, models based on quantum neural networks (QNNs) can suffer from excessive local minima and barren plateaus in their training landscapes. Recently, the nascent field of geometric quantum machine learning (GQML) has emerged as a potential solution to some of those issues. The key insight of GQML is that one should design architectures, such as equivariant QNNs, encoding the symmetries of the problem at hand. Here, we focus on problems with permutation symmetry (i.e., the group of symmetry $S_n$), and show how to build $S_n$-equivariant QNNs. We provide an analytical study of their performance, proving that they do not suffer from barren plateaus, quickly reach overparametrization, and can generalize well from small amounts of data. To verify our results, we perform numerical simulations for a graph state classification task. Our work provides the first theoretical guarantees for equivariant QNNs, thus indicating the extreme power and potential of GQML.

Theory for Equivariant Quantum Neural Networks

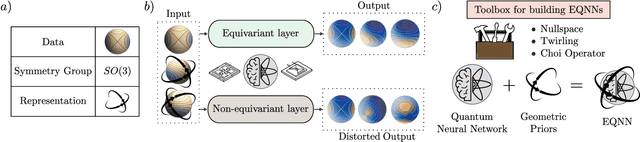
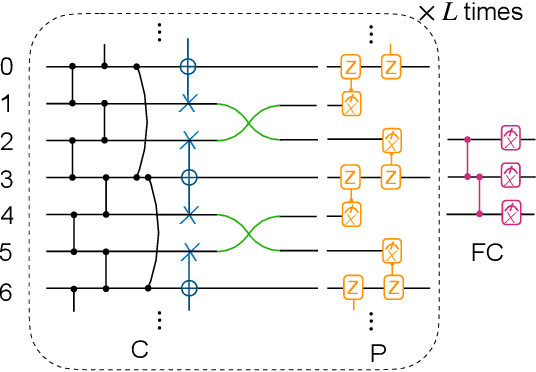
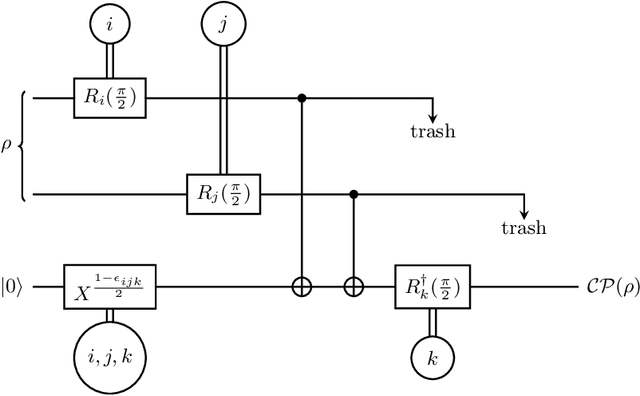
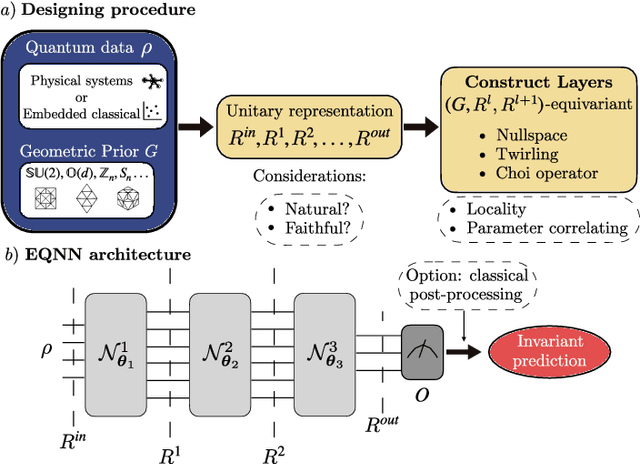
Most currently used quantum neural network architectures have little-to-no inductive biases, leading to trainability and generalization issues. Inspired by a similar problem, recent breakthroughs in classical machine learning address this crux by creating models encoding the symmetries of the learning task. This is materialized through the usage of equivariant neural networks whose action commutes with that of the symmetry. In this work, we import these ideas to the quantum realm by presenting a general theoretical framework to understand, classify, design and implement equivariant quantum neural networks. As a special implementation, we show how standard quantum convolutional neural networks (QCNN) can be generalized to group-equivariant QCNNs where both the convolutional and pooling layers are equivariant under the relevant symmetry group. Our framework can be readily applied to virtually all areas of quantum machine learning, and provides hope to alleviate central challenges such as barren plateaus, poor local minima, and sample complexity.

Representation Theory for Geometric Quantum Machine Learning

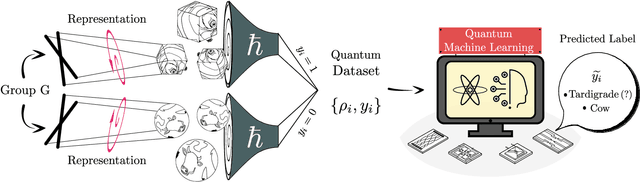
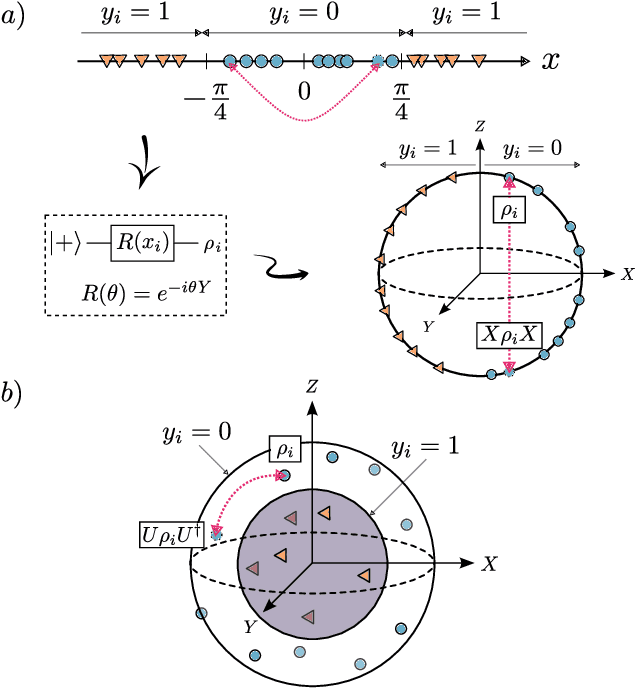
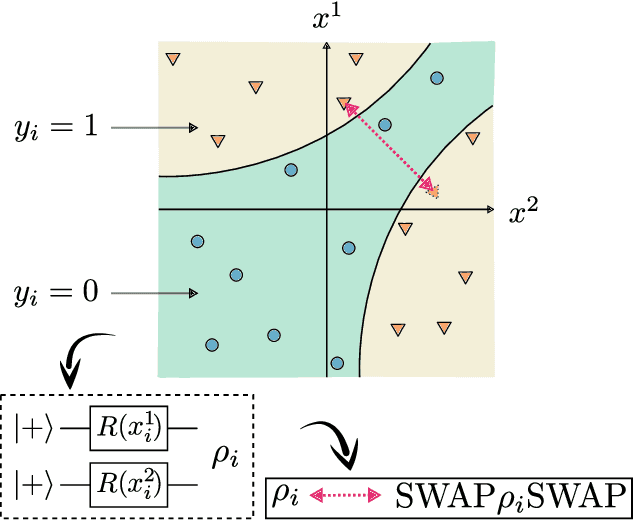
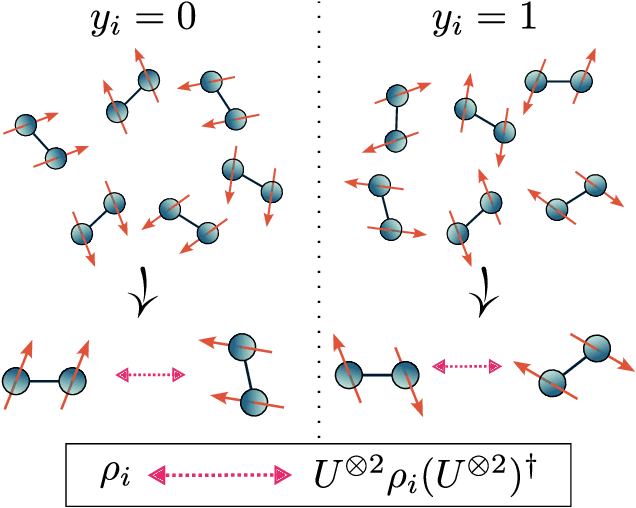
Recent advances in classical machine learning have shown that creating models with inductive biases encoding the symmetries of a problem can greatly improve performance. Importation of these ideas, combined with an existing rich body of work at the nexus of quantum theory and symmetry, has given rise to the field of Geometric Quantum Machine Learning (GQML). Following the success of its classical counterpart, it is reasonable to expect that GQML will play a crucial role in developing problem-specific and quantum-aware models capable of achieving a computational advantage. Despite the simplicity of the main idea of GQML -- create architectures respecting the symmetries of the data -- its practical implementation requires a significant amount of knowledge of group representation theory. We present an introduction to representation theory tools from the optics of quantum learning, driven by key examples involving discrete and continuous groups. These examples are sewn together by an exposition outlining the formal capture of GQML symmetries via "label invariance under the action of a group representation", a brief (but rigorous) tour through finite and compact Lie group representation theory, a reexamination of ubiquitous tools like Haar integration and twirling, and an overview of some successful strategies for detecting symmetries.

Entangled Datasets for Quantum Machine Learning

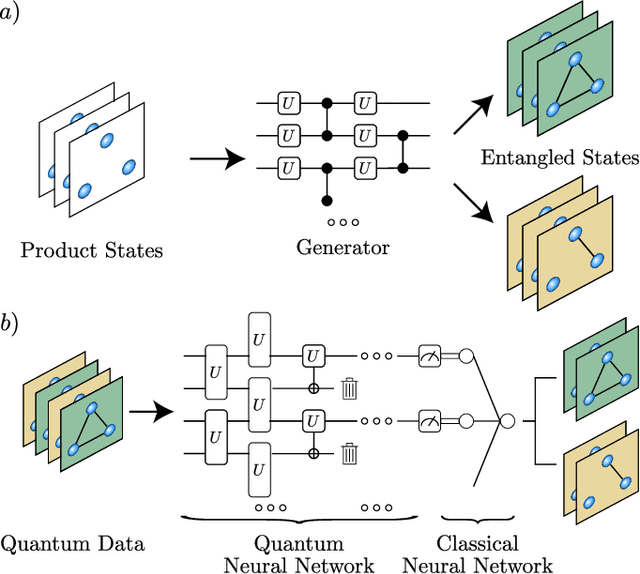
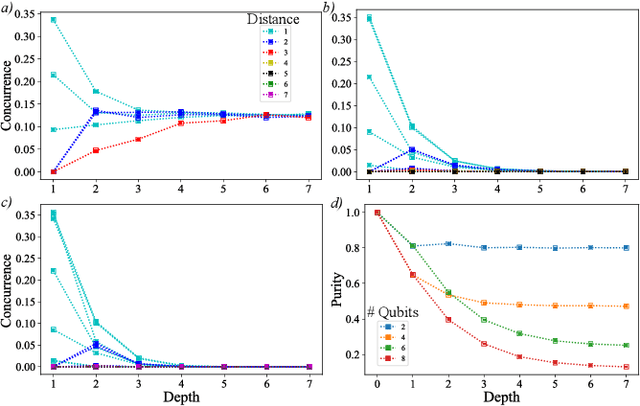
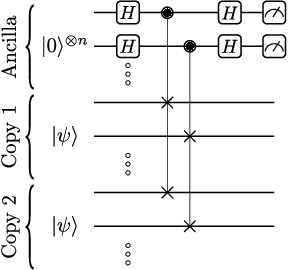
High-quality, large-scale datasets have played a crucial role in the development and success of classical machine learning. Quantum Machine Learning (QML) is a new field that aims to use quantum computers for data analysis, with the hope of obtaining a quantum advantage of some sort. While most proposed QML architectures are benchmarked using classical datasets, there is still doubt whether QML on classical datasets will achieve such an advantage. In this work, we argue that one should instead employ quantum datasets composed of quantum states. For this purpose, we introduce the NTangled dataset composed of quantum states with different amounts and types of multipartite entanglement. We first show how a quantum neural network can be trained to generate the states in the NTangled dataset. Then, we use the NTangled dataset to benchmark QML models for supervised learning classification tasks. We also consider an alternative entanglement-based dataset, which is scalable and is composed of states prepared by quantum circuits with different depths. As a byproduct of our results, we introduce a novel method for generating multipartite entangled states, providing a use-case of quantum neural networks for quantum entanglement theory.