A Review of Barren Plateaus in Variational Quantum Computing

Variational quantum computing offers a flexible computational paradigm with applications in diverse areas. However, a key obstacle to realizing their potential is the Barren Plateau (BP) phenomenon. When a model exhibits a BP, its parameter optimization landscape becomes exponentially flat and featureless as the problem size increases. Importantly, all the moving pieces of an algorithm -- choices of ansatz, initial state, observable, loss function and hardware noise -- can lead to BPs when ill-suited. Due to the significant impact of BPs on trainability, researchers have dedicated considerable effort to develop theoretical and heuristic methods to understand and mitigate their effects. As a result, the study of BPs has become a thriving area of research, influencing and cross-fertilizing other fields such as quantum optimal control, tensor networks, and learning theory. This article provides a comprehensive review of the current understanding of the BP phenomenon.

Does provable absence of barren plateaus imply classical simulability? Or, why we need to rethink variational quantum computing

A large amount of effort has recently been put into understanding the barren plateau phenomenon. In this perspective article, we face the increasingly loud elephant in the room and ask a question that has been hinted at by many but not explicitly addressed: Can the structure that allows one to avoid barren plateaus also be leveraged to efficiently simulate the loss classically? We present strong evidence that commonly used models with provable absence of barren plateaus are also classically simulable, provided that one can collect some classical data from quantum devices during an initial data acquisition phase. This follows from the observation that barren plateaus result from a curse of dimensionality, and that current approaches for solving them end up encoding the problem into some small, classically simulable, subspaces. This sheds serious doubt on the non-classicality of the information processing capabilities of parametrized quantum circuits for barren plateau-free landscapes and on the possibility of superpolynomial advantages from running them on quantum hardware. We end by discussing caveats in our arguments, the role of smart initializations, and by highlighting new opportunities that our perspective raises.

Deep quantum neural networks form Gaussian processes

It is well known that artificial neural networks initialized from independent and identically distributed priors converge to Gaussian processes in the limit of large number of neurons per hidden layer. In this work we prove an analogous result for Quantum Neural Networks (QNNs). Namely, we show that the outputs of certain models based on Haar random unitary or orthogonal deep QNNs converge to Gaussian processes in the limit of large Hilbert space dimension $d$. The derivation of this result is more nuanced than in the classical case due the role played by the input states, the measurement observable, and the fact that the entries of unitary matrices are not independent. An important consequence of our analysis is that the ensuing Gaussian processes cannot be used to efficiently predict the outputs of the QNN via Bayesian statistics. Furthermore, our theorems imply that the concentration of measure phenomenon in Haar random QNNs is much worse than previously thought, as we prove that expectation values and gradients concentrate as $\mathcal{O}\left(\frac{1}{e^d \sqrt{d}}\right)$ -- exponentially in the Hilbert space dimension. Finally, we discuss how our results improve our understanding of concentration in $t$-designs.

On the universality of $S_n$-equivariant $k$-body gates

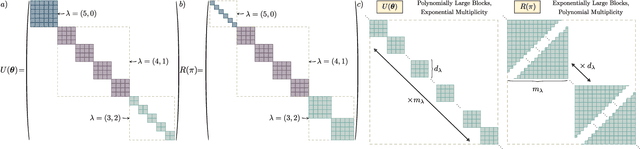
The importance of symmetries has recently been recognized in quantum machine learning from the simple motto: if a task exhibits a symmetry (given by a group $\mathfrak{G}$), the learning model should respect said symmetry. This can be instantiated via $\mathfrak{G}$-equivariant Quantum Neural Networks (QNNs), i.e., parametrized quantum circuits whose gates are generated by operators commuting with a given representation of $\mathfrak{G}$. In practice, however, there might be additional restrictions to the types of gates one can use, such as being able to act on at most $k$ qubits. In this work we study how the interplay between symmetry and $k$-bodyness in the QNN generators affect its expressiveness for the special case of $\mathfrak{G}=S_n$, the symmetric group. Our results show that if the QNN is generated by one- and two-body $S_n$-equivariant gates, the QNN is semi-universal but not universal. That is, the QNN can generate any arbitrary special unitary matrix in the invariant subspaces, but has no control over the relative phases between them. Then, we show that in order to reach universality one needs to include $n$-body generators (if $n$ is even) or $(n-1)$-body generators (if $n$ is odd). As such, our results brings us a step closer to better understanding the capabilities and limitations of equivariant QNNs.

Effects of noise on the overparametrization of quantum neural networks

Overparametrization is one of the most surprising and notorious phenomena in machine learning. Recently, there have been several efforts to study if, and how, Quantum Neural Networks (QNNs) acting in the absence of hardware noise can be overparametrized. In particular, it has been proposed that a QNN can be defined as overparametrized if it has enough parameters to explore all available directions in state space. That is, if the rank of the Quantum Fisher Information Matrix (QFIM) for the QNN's output state is saturated. Here, we explore how the presence of noise affects the overparametrization phenomenon. Our results show that noise can "turn on" previously-zero eigenvalues of the QFIM. This enables the parametrized state to explore directions that were otherwise inaccessible, thus potentially turning an overparametrized QNN into an underparametrized one. For small noise levels, the QNN is quasi-overparametrized, as large eigenvalues coexists with small ones. Then, we prove that as the magnitude of noise increases all the eigenvalues of the QFIM become exponentially suppressed, indicating that the state becomes insensitive to any change in the parameters. As such, there is a pull-and-tug effect where noise can enable new directions, but also suppress the sensitivity to parameter updates. Finally, our results imply that current QNN capacity measures are ill-defined when hardware noise is present.

Theoretical Guarantees for Permutation-Equivariant Quantum Neural Networks

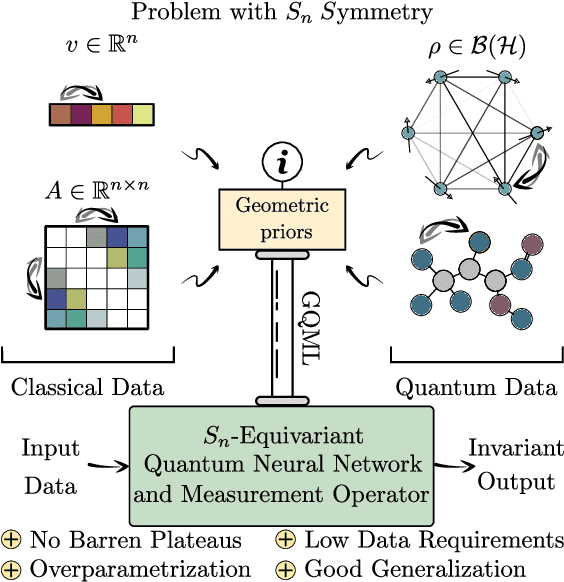
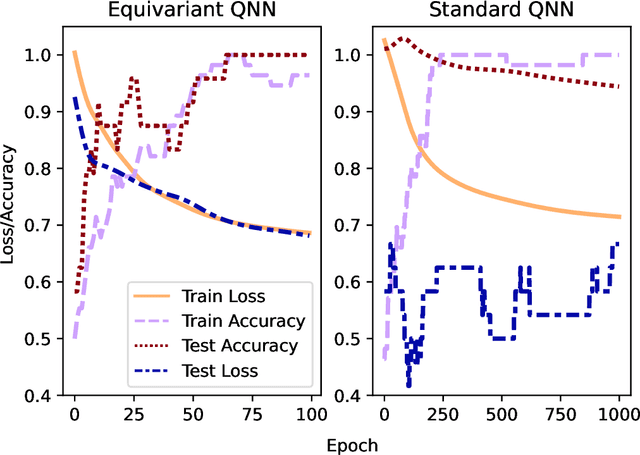
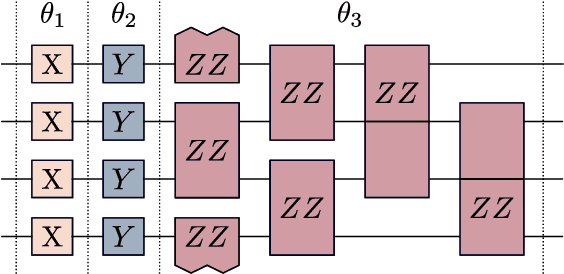
Despite the great promise of quantum machine learning models, there are several challenges one must overcome before unlocking their full potential. For instance, models based on quantum neural networks (QNNs) can suffer from excessive local minima and barren plateaus in their training landscapes. Recently, the nascent field of geometric quantum machine learning (GQML) has emerged as a potential solution to some of those issues. The key insight of GQML is that one should design architectures, such as equivariant QNNs, encoding the symmetries of the problem at hand. Here, we focus on problems with permutation symmetry (i.e., the group of symmetry $S_n$), and show how to build $S_n$-equivariant QNNs. We provide an analytical study of their performance, proving that they do not suffer from barren plateaus, quickly reach overparametrization, and can generalize well from small amounts of data. To verify our results, we perform numerical simulations for a graph state classification task. Our work provides the first theoretical guarantees for equivariant QNNs, thus indicating the extreme power and potential of GQML.

Theory for Equivariant Quantum Neural Networks

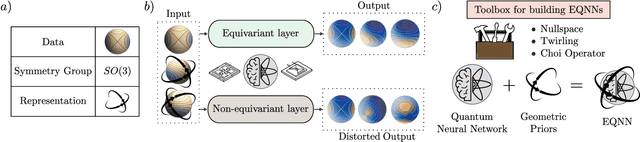
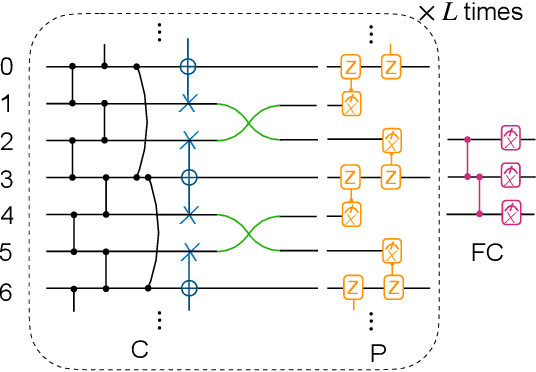
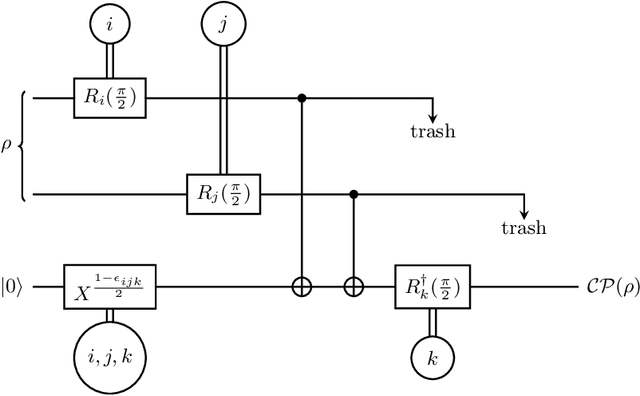
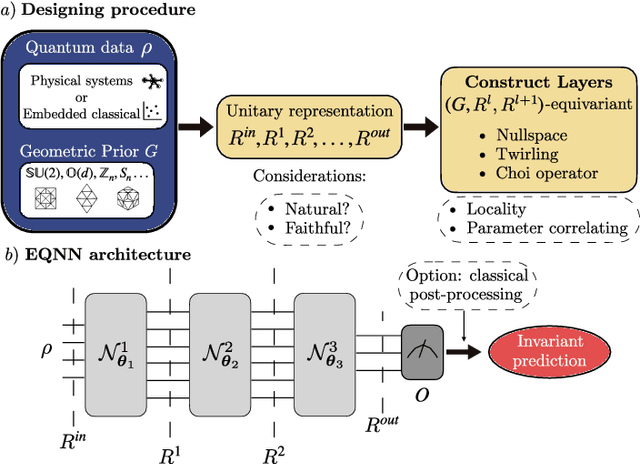
Most currently used quantum neural network architectures have little-to-no inductive biases, leading to trainability and generalization issues. Inspired by a similar problem, recent breakthroughs in classical machine learning address this crux by creating models encoding the symmetries of the learning task. This is materialized through the usage of equivariant neural networks whose action commutes with that of the symmetry. In this work, we import these ideas to the quantum realm by presenting a general theoretical framework to understand, classify, design and implement equivariant quantum neural networks. As a special implementation, we show how standard quantum convolutional neural networks (QCNN) can be generalized to group-equivariant QCNNs where both the convolutional and pooling layers are equivariant under the relevant symmetry group. Our framework can be readily applied to virtually all areas of quantum machine learning, and provides hope to alleviate central challenges such as barren plateaus, poor local minima, and sample complexity.

Representation Theory for Geometric Quantum Machine Learning

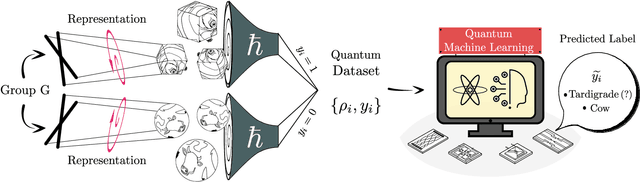
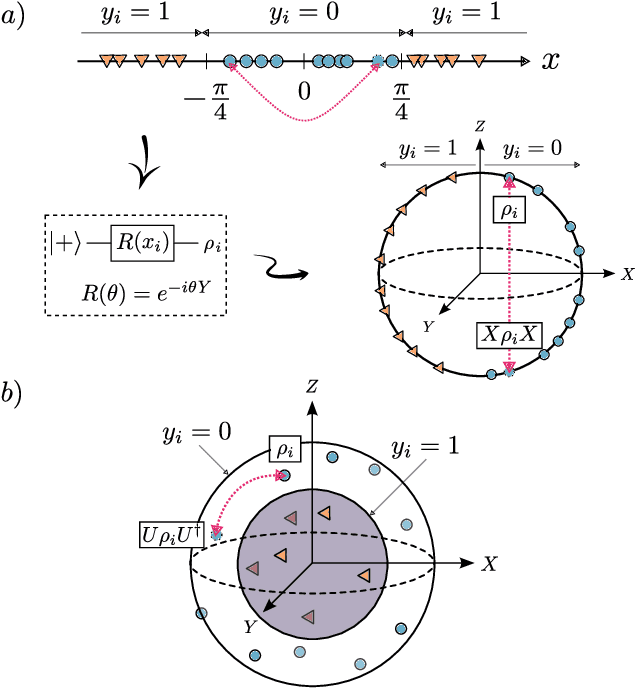
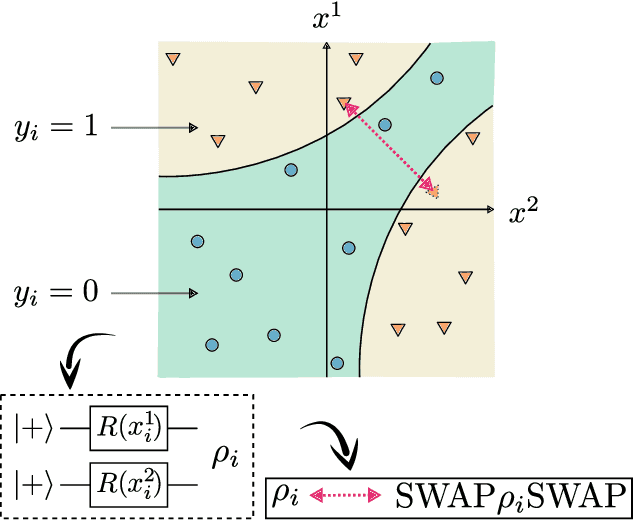
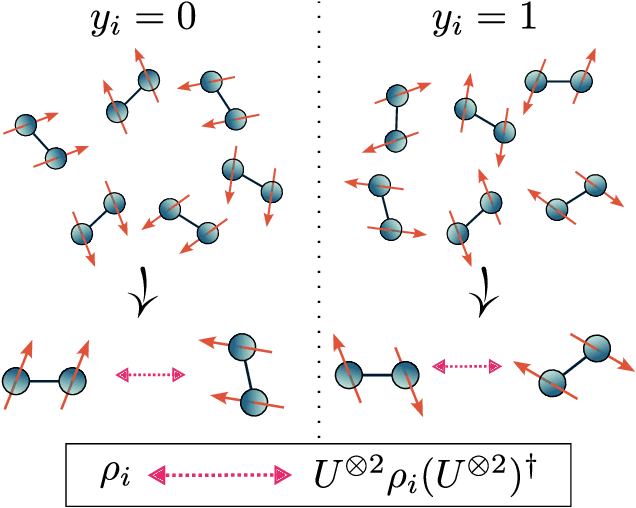
Recent advances in classical machine learning have shown that creating models with inductive biases encoding the symmetries of a problem can greatly improve performance. Importation of these ideas, combined with an existing rich body of work at the nexus of quantum theory and symmetry, has given rise to the field of Geometric Quantum Machine Learning (GQML). Following the success of its classical counterpart, it is reasonable to expect that GQML will play a crucial role in developing problem-specific and quantum-aware models capable of achieving a computational advantage. Despite the simplicity of the main idea of GQML -- create architectures respecting the symmetries of the data -- its practical implementation requires a significant amount of knowledge of group representation theory. We present an introduction to representation theory tools from the optics of quantum learning, driven by key examples involving discrete and continuous groups. These examples are sewn together by an exposition outlining the formal capture of GQML symmetries via "label invariance under the action of a group representation", a brief (but rigorous) tour through finite and compact Lie group representation theory, a reexamination of ubiquitous tools like Haar integration and twirling, and an overview of some successful strategies for detecting symmetries.

Group-Invariant Quantum Machine Learning

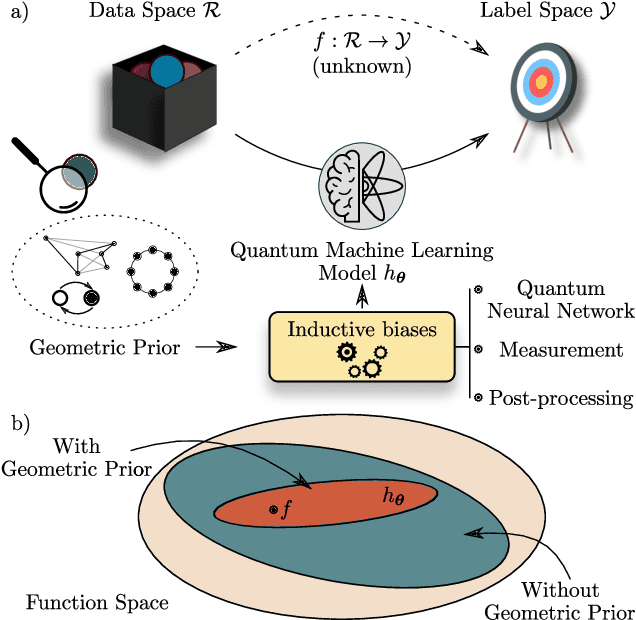
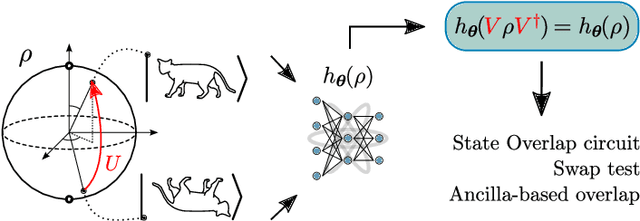
Quantum Machine Learning (QML) models are aimed at learning from data encoded in quantum states. Recently, it has been shown that models with little to no inductive biases (i.e., with no assumptions about the problem embedded in the model) are likely to have trainability and generalization issues, especially for large problem sizes. As such, it is fundamental to develop schemes that encode as much information as available about the problem at hand. In this work we present a simple, yet powerful, framework where the underlying invariances in the data are used to build QML models that, by construction, respect those symmetries. These so-called group-invariant models produce outputs that remain invariant under the action of any element of the symmetry group $\mathfrak{G}$ associated to the dataset. We present theoretical results underpinning the design of $\mathfrak{G}$-invariant models, and exemplify their application through several paradigmatic QML classification tasks including cases when $\mathfrak{G}$ is a continuous Lie group and also when it is a discrete symmetry group. Notably, our framework allows us to recover, in an elegant way, several well known algorithms for the literature, as well as to discover new ones. Taken together, we expect that our results will help pave the way towards a more geometric and group-theoretic approach to QML model design.

Theory of overparametrization in quantum neural networks

The prospect of achieving quantum advantage with Quantum Neural Networks (QNNs) is exciting. Understanding how QNN properties (e.g., the number of parameters $M$) affect the loss landscape is crucial to the design of scalable QNN architectures. Here, we rigorously analyze the overparametrization phenomenon in QNNs with periodic structure. We define overparametrization as the regime where the QNN has more than a critical number of parameters $M_c$ that allows it to explore all relevant directions in state space. Our main results show that the dimension of the Lie algebra obtained from the generators of the QNN is an upper bound for $M_c$, and for the maximal rank that the quantum Fisher information and Hessian matrices can reach. Underparametrized QNNs have spurious local minima in the loss landscape that start disappearing when $M\geq M_c$. Thus, the overparametrization onset corresponds to a computational phase transition where the QNN trainability is greatly improved by a more favorable landscape. We then connect the notion of overparametrization to the QNN capacity, so that when a QNN is overparametrized, its capacity achieves its maximum possible value. We run numerical simulations for eigensolver, compilation, and autoencoding applications to showcase the overparametrization computational phase transition. We note that our results also apply to variational quantum algorithms and quantum optimal control.