Quantum advantage for learning shallow neural networks with natural data distributions

The application of quantum computers to machine learning tasks is an exciting potential direction to explore in search of quantum advantage. In the absence of large quantum computers to empirically evaluate performance, theoretical frameworks such as the quantum probably approximately correct (PAC) and quantum statistical query (QSQ) models have been proposed to study quantum algorithms for learning classical functions. Despite numerous works investigating quantum advantage in these models, we nevertheless only understand it at two extremes: either exponential quantum advantages for uniform input distributions or no advantage for potentially adversarial distributions. In this work, we study the gap between these two regimes by designing an efficient quantum algorithm for learning periodic neurons in the QSQ model over a broad range of non-uniform distributions, which includes Gaussian, generalized Gaussian, and logistic distributions. To our knowledge, our work is also the first result in quantum learning theory for classical functions that explicitly considers real-valued functions. Recent advances in classical learning theory prove that learning periodic neurons is hard for any classical gradient-based algorithm, giving us an exponential quantum advantage over such algorithms, which are the standard workhorses of machine learning. Moreover, in some parameter regimes, the problem remains hard for classical statistical query algorithms and even general classical algorithms learning under small amounts of noise.

A Review of Barren Plateaus in Variational Quantum Computing

Variational quantum computing offers a flexible computational paradigm with applications in diverse areas. However, a key obstacle to realizing their potential is the Barren Plateau (BP) phenomenon. When a model exhibits a BP, its parameter optimization landscape becomes exponentially flat and featureless as the problem size increases. Importantly, all the moving pieces of an algorithm -- choices of ansatz, initial state, observable, loss function and hardware noise -- can lead to BPs when ill-suited. Due to the significant impact of BPs on trainability, researchers have dedicated considerable effort to develop theoretical and heuristic methods to understand and mitigate their effects. As a result, the study of BPs has become a thriving area of research, influencing and cross-fertilizing other fields such as quantum optimal control, tensor networks, and learning theory. This article provides a comprehensive review of the current understanding of the BP phenomenon.

Learning shallow quantum circuits

Despite fundamental interests in learning quantum circuits, the existence of a computationally efficient algorithm for learning shallow quantum circuits remains an open question. Because shallow quantum circuits can generate distributions that are classically hard to sample from, existing learning algorithms do not apply. In this work, we present a polynomial-time classical algorithm for learning the description of any unknown $n$-qubit shallow quantum circuit $U$ (with arbitrary unknown architecture) within a small diamond distance using single-qubit measurement data on the output states of $U$. We also provide a polynomial-time classical algorithm for learning the description of any unknown $n$-qubit state $\lvert \psi \rangle = U \lvert 0^n \rangle$ prepared by a shallow quantum circuit $U$ (on a 2D lattice) within a small trace distance using single-qubit measurements on copies of $\lvert \psi \rangle$. Our approach uses a quantum circuit representation based on local inversions and a technique to combine these inversions. This circuit representation yields an optimization landscape that can be efficiently navigated and enables efficient learning of quantum circuits that are classically hard to simulate.

Exponential Quantum Communication Advantage in Distributed Learning

Training and inference with large machine learning models that far exceed the memory capacity of individual devices necessitates the design of distributed architectures, forcing one to contend with communication constraints. We present a framework for distributed computation over a quantum network in which data is encoded into specialized quantum states. We prove that for certain models within this framework, inference and training using gradient descent can be performed with exponentially less communication compared to their classical analogs, and with relatively modest time and space complexity overheads relative to standard gradient-based methods. To our knowledge, this is the first example of exponential quantum advantage for a generic class of machine learning problems with dense classical data that holds regardless of the data encoding cost. Moreover, we show that models in this class can encode highly nonlinear features of their inputs, and their expressivity increases exponentially with model depth. We also find that, interestingly, the communication advantage nearly vanishes for simpler linear classifiers. These results can be combined with natural privacy advantages in the communicated quantum states that limit the amount of information that can be extracted from them about the data and model parameters. Taken as a whole, these findings form a promising foundation for distributed machine learning over quantum networks.

On quantum backpropagation, information reuse, and cheating measurement collapse

The success of modern deep learning hinges on the ability to train neural networks at scale. Through clever reuse of intermediate information, backpropagation facilitates training through gradient computation at a total cost roughly proportional to running the function, rather than incurring an additional factor proportional to the number of parameters - which can now be in the trillions. Naively, one expects that quantum measurement collapse entirely rules out the reuse of quantum information as in backpropagation. But recent developments in shadow tomography, which assumes access to multiple copies of a quantum state, have challenged that notion. Here, we investigate whether parameterized quantum models can train as efficiently as classical neural networks. We show that achieving backpropagation scaling is impossible without access to multiple copies of a state. With this added ability, we introduce an algorithm with foundations in shadow tomography that matches backpropagation scaling in quantum resources while reducing classical auxiliary computational costs to open problems in shadow tomography. These results highlight the nuance of reusing quantum information for practical purposes and clarify the unique difficulties in training large quantum models, which could alter the course of quantum machine learning.

Revisiting dequantization and quantum advantage in learning tasks

It has been shown that the apparent advantage of some quantum machine learning algorithms may be efficiently replicated using classical algorithms with suitable data access -- a process known as dequantization. Existing works on dequantization compare quantum algorithms which take copies of an n-qubit quantum state $|x\rangle = \sum_{i} x_i |i\rangle$ as input to classical algorithms which have sample and query (SQ) access to the vector $x$. In this note, we prove that classical algorithms with SQ access can accomplish some learning tasks exponentially faster than quantum algorithms with quantum state inputs. Because classical algorithms are a subset of quantum algorithms, this demonstrates that SQ access can sometimes be significantly more powerful than quantum state inputs. Our findings suggest that the absence of exponential quantum advantage in some learning tasks may be due to SQ access being too powerful relative to quantum state inputs. If we compare quantum algorithms with quantum state inputs to classical algorithms with access to measurement data on quantum states, the landscape of quantum advantage can be dramatically different. We remark that when the quantum states are constructed from exponential-size classical data, comparing SQ access and quantum state inputs is appropriate since both require exponential time to prepare.

Quantum advantage in learning from experiments

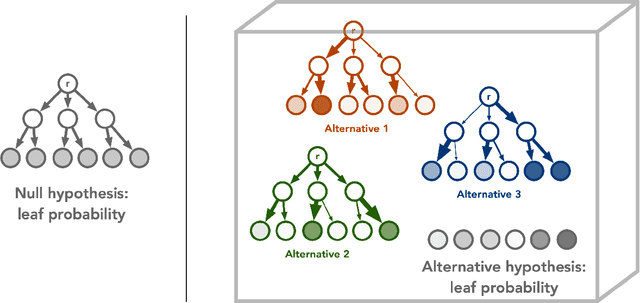
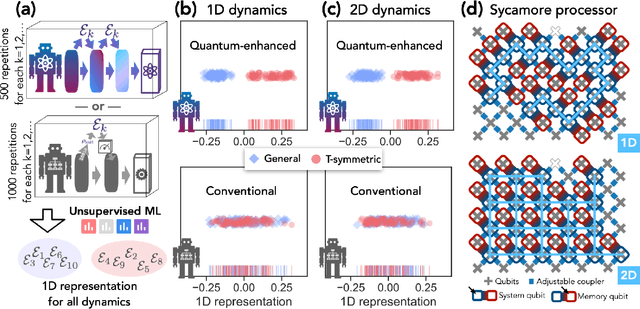
Quantum technology has the potential to revolutionize how we acquire and process experimental data to learn about the physical world. An experimental setup that transduces data from a physical system to a stable quantum memory, and processes that data using a quantum computer, could have significant advantages over conventional experiments in which the physical system is measured and the outcomes are processed using a classical computer. We prove that, in various tasks, quantum machines can learn from exponentially fewer experiments than those required in conventional experiments. The exponential advantage holds in predicting properties of physical systems, performing quantum principal component analysis on noisy states, and learning approximate models of physical dynamics. In some tasks, the quantum processing needed to achieve the exponential advantage can be modest; for example, one can simultaneously learn about many noncommuting observables by processing only two copies of the system. Conducting experiments with up to 40 superconducting qubits and 1300 quantum gates, we demonstrate that a substantial quantum advantage can be realized using today's relatively noisy quantum processors. Our results highlight how quantum technology can enable powerful new strategies to learn about nature.

Variational Quantum Algorithms

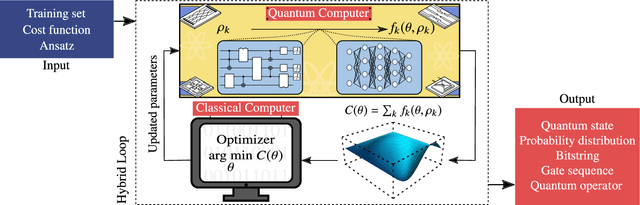
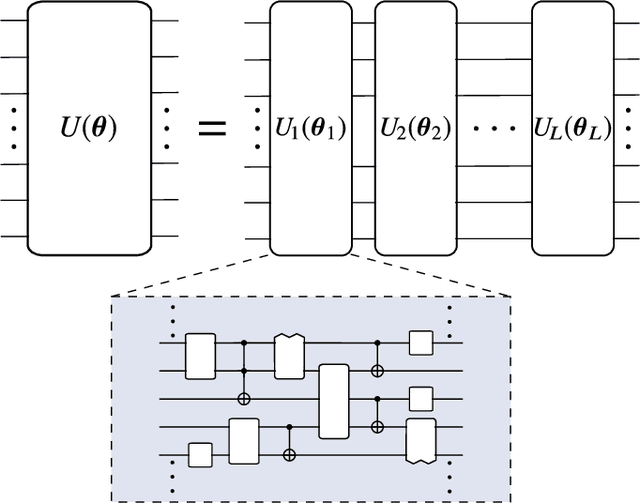
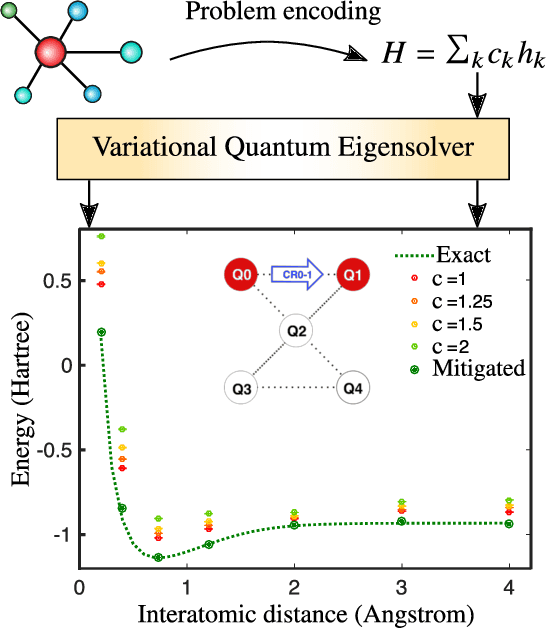
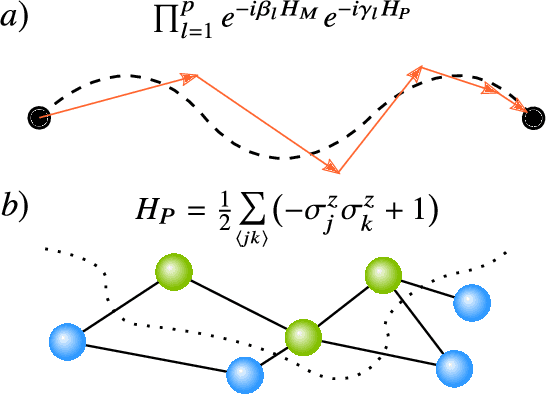
Applications such as simulating large quantum systems or solving large-scale linear algebra problems are immensely challenging for classical computers due their extremely high computational cost. Quantum computers promise to unlock these applications, although fault-tolerant quantum computers will likely not be available for several years. Currently available quantum devices have serious constraints, including limited qubit numbers and noise processes that limit circuit depth. Variational Quantum Algorithms (VQAs), which employ a classical optimizer to train a parametrized quantum circuit, have emerged as a leading strategy to address these constraints. VQAs have now been proposed for essentially all applications that researchers have envisioned for quantum computers, and they appear to the best hope for obtaining quantum advantage. Nevertheless, challenges remain including the trainability, accuracy, and efficiency of VQAs. In this review article we present an overview of the field of VQAs. Furthermore, we discuss strategies to overcome their challenges as well as the exciting prospects for using them as a means to obtain quantum advantage.

Power of data in quantum machine learning

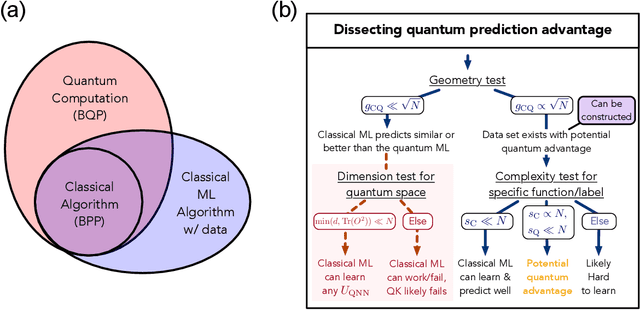
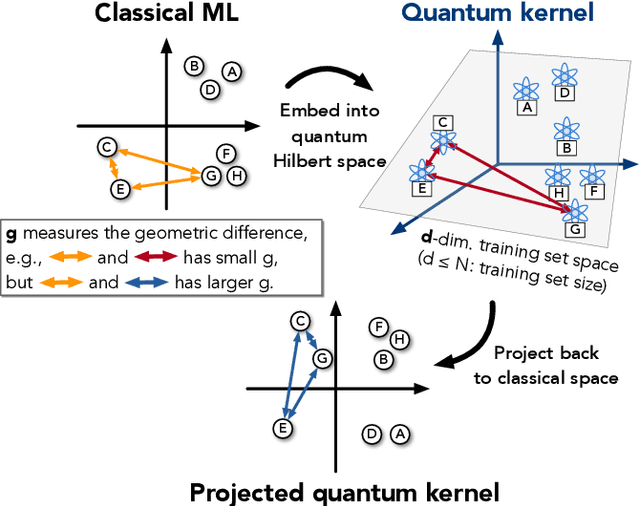
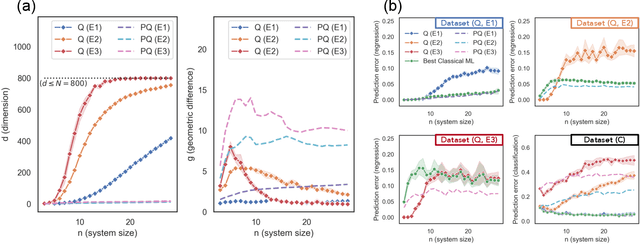
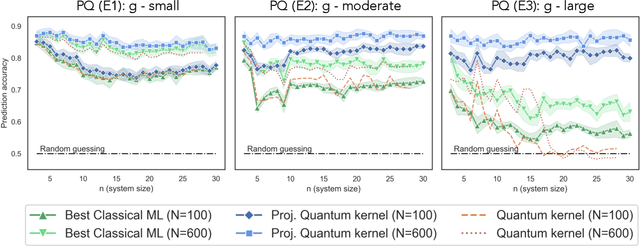
The use of quantum computing for machine learning is among the most exciting prospective applications of quantum technologies. At the crux of excitement is the potential for quantum computers to perform some computations exponentially faster than their classical counterparts. However, a machine learning task where some data is provided can be considerably different than more commonly studied computational tasks. In this work, we show that some problems that are classically hard to compute can be predicted easily with classical machines that learn from data. We find that classical machines can often compete or outperform existing quantum models even on data sets generated by quantum evolution, especially at large system sizes. Using rigorous prediction error bounds as a foundation, we develop a methodology for assessing the potential for quantum advantage in prediction on learning tasks. We show how the use of exponentially large quantum Hilbert space in existing quantum models can result in significantly inferior prediction performance compared to classical machines. To circumvent the observed setbacks, we propose an improvement by projecting all quantum states to an approximate classical representation. The projected quantum model provides a simple and rigorous quantum speed-up for a recently proposed learning problem in the fault-tolerant regime. For more near-term quantum models, the projected versions demonstrate a significant prediction advantage over some classical models on engineered data sets in one of the largest numerical tests for gate-based quantum machine learning to date, up to 30 qubits.

Layerwise learning for quantum neural networks

With the increased focus on quantum circuit learning for near-term applications on quantum devices, in conjunction with unique challenges presented by cost function landscapes of parametrized quantum circuits, strategies for effective training are becoming increasingly important. In order to ameliorate some of these challenges, we investigate a layerwise learning strategy for parametrized quantum circuits. The circuit depth is incrementally grown during optimization, and only subsets of parameters are updated in each training step. We show that when considering sampling noise, this strategy can help avoid the problem of barren plateaus of the error surface due to the low depth of circuits, low number of parameters trained in one step, and larger magnitude of gradients compared to training the full circuit. These properties make our algorithm preferable for execution on noisy intermediate-scale quantum devices. We demonstrate our approach on an image-classification task on handwritten digits, and show that layerwise learning attains an 8% lower generalization error on average in comparison to standard learning schemes for training quantum circuits of the same size. Additionally, the percentage of runs that reach lower test errors is up to 40% larger compared to training the full circuit, which is susceptible to creeping onto a plateau during training.