Andrea Skolik
Equivariant quantum circuits for learning on weighted graphs
May 12, 2022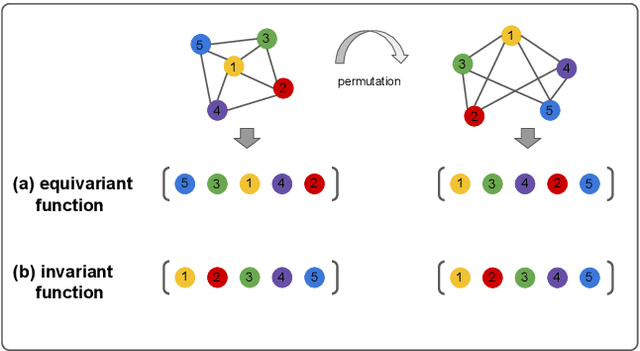
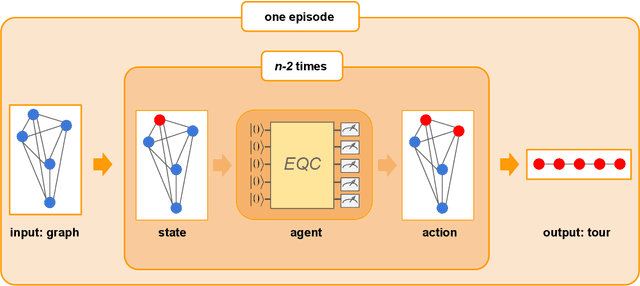
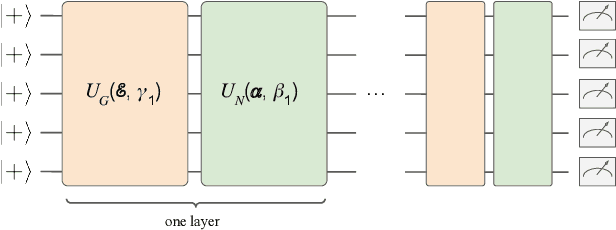
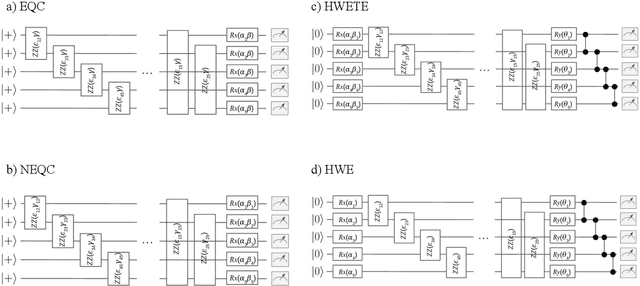
Abstract:Variational quantum algorithms are the leading candidate for near-term advantage on noisy quantum hardware. When training a parametrized quantum circuit to solve a specific task, the choice of ansatz is one of the most important factors that determines the trainability and performance of the algorithm. Problem-tailored ansatzes have become the standard for tasks in optimization or quantum chemistry, and yield more efficient algorithms with better performance than unstructured approaches. In quantum machine learning (QML), however, the literature on ansatzes that are motivated by the training data structure is scarce. Considering that it is widely known that unstructured ansatzes can become untrainable with increasing system size and circuit depth, it is of key importance to also study problem-tailored circuit architectures in a QML context. In this work, we introduce an ansatz for learning tasks on weighted graphs that respects an important graph symmetry, namely equivariance under node permutations. We evaluate the performance of this ansatz on a complex learning task on weighted graphs, where a ML model is used to implement a heuristic for a combinatorial optimization problem. We analytically study the expressivity of our ansatz at depth one, and numerically compare the performance of our model on instances with up to 20 qubits to ansatzes where the equivariance property is gradually broken. We show that our ansatz outperforms all others even in the small-instance regime. Our results strengthen the notion that symmetry-preserving ansatzes are a key to success in QML and should be an active area of research in order to enable near-term advantages in this field.
Hyperparameter optimization of hybrid quantum neural networks for car classification
May 10, 2022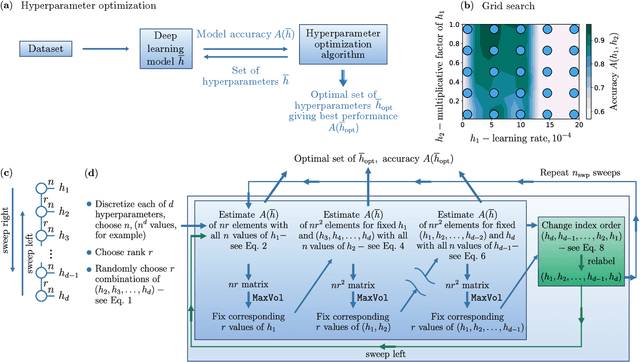

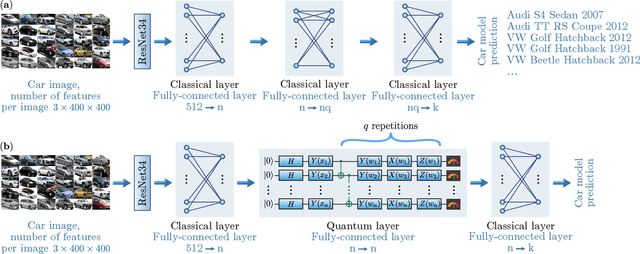
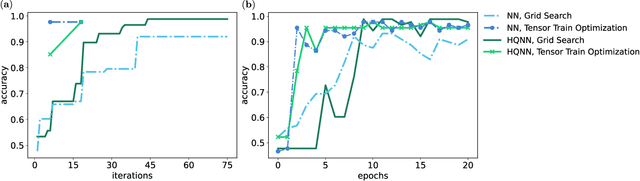
Abstract:Image recognition is one of the primary applications of machine learning algorithms. Nevertheless, machine learning models used in modern image recognition systems consist of millions of parameters that usually require significant computational time to be adjusted. Moreover, adjustment of model hyperparameters leads to additional overhead. Because of this, new developments in machine learning models and hyperparameter optimization techniques are required. This paper presents a quantum-inspired hyperparameter optimization technique and a hybrid quantum-classical machine learning model for supervised learning. We benchmark our hyperparameter optimization method over standard black-box objective functions and observe performance improvements in the form of reduced expected run times and fitness in response to the growth in the size of the search space. We test our approaches in a car image classification task, and demonstrate a full-scale implementation of the hybrid quantum neural network model with the tensor train hyperparameter optimization. Our tests show a qualitative and quantitative advantage over the corresponding standard classical tabular grid search approach used with a deep neural network ResNet34. A classification accuracy of 0.97 was obtained by the hybrid model after 18 iterations, whereas the classical model achieved an accuracy of 0.92 after 75 iterations.
Layerwise learning for quantum neural networks
Jun 26, 2020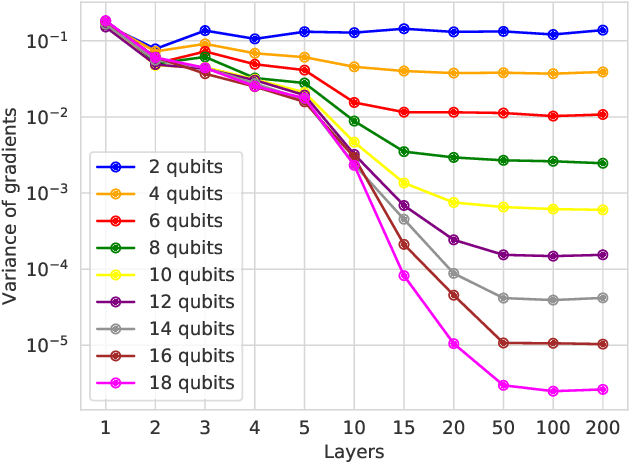
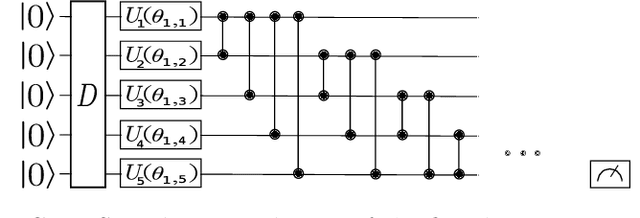
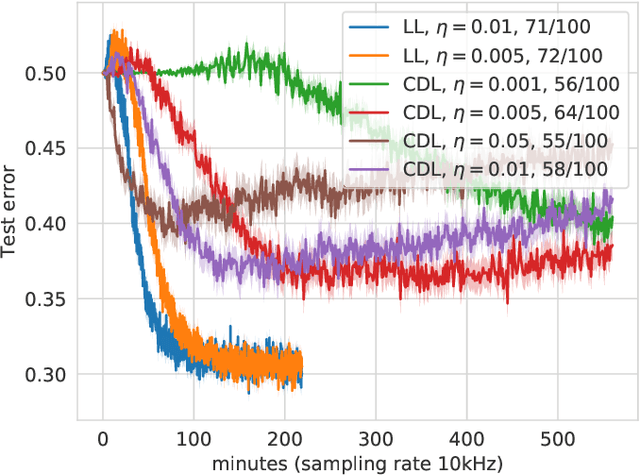
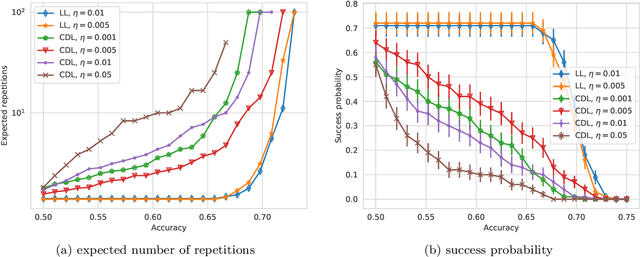
Abstract:With the increased focus on quantum circuit learning for near-term applications on quantum devices, in conjunction with unique challenges presented by cost function landscapes of parametrized quantum circuits, strategies for effective training are becoming increasingly important. In order to ameliorate some of these challenges, we investigate a layerwise learning strategy for parametrized quantum circuits. The circuit depth is incrementally grown during optimization, and only subsets of parameters are updated in each training step. We show that when considering sampling noise, this strategy can help avoid the problem of barren plateaus of the error surface due to the low depth of circuits, low number of parameters trained in one step, and larger magnitude of gradients compared to training the full circuit. These properties make our algorithm preferable for execution on noisy intermediate-scale quantum devices. We demonstrate our approach on an image-classification task on handwritten digits, and show that layerwise learning attains an 8% lower generalization error on average in comparison to standard learning schemes for training quantum circuits of the same size. Additionally, the percentage of runs that reach lower test errors is up to 40% larger compared to training the full circuit, which is susceptible to creeping onto a plateau during training.
TensorFlow Quantum: A Software Framework for Quantum Machine Learning
Mar 06, 2020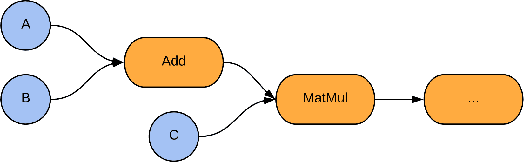
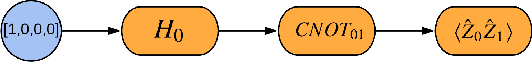
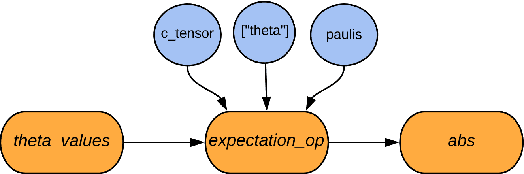
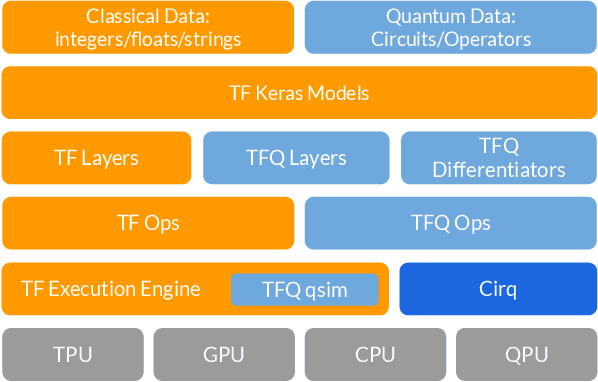
Abstract:We introduce TensorFlow Quantum (TFQ), an open source library for the rapid prototyping of hybrid quantum-classical models for classical or quantum data. This framework offers high-level abstractions for the design and training of both discriminative and generative quantum models under TensorFlow and supports high-performance quantum circuit simulators. We provide an overview of the software architecture and building blocks through several examples and review the theory of hybrid quantum-classical neural networks. We illustrate TFQ functionalities via several basic applications including supervised learning for quantum classification, quantum control, and quantum approximate optimization. Moreover, we demonstrate how one can apply TFQ to tackle advanced quantum learning tasks including meta-learning, Hamiltonian learning, and sampling thermal states. We hope this framework provides the necessary tools for the quantum computing and machine learning research communities to explore models of both natural and artificial quantum systems, and ultimately discover new quantum algorithms which could potentially yield a quantum advantage.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge