Quantum-Enhanced Selection Operators for Evolutionary Algorithms

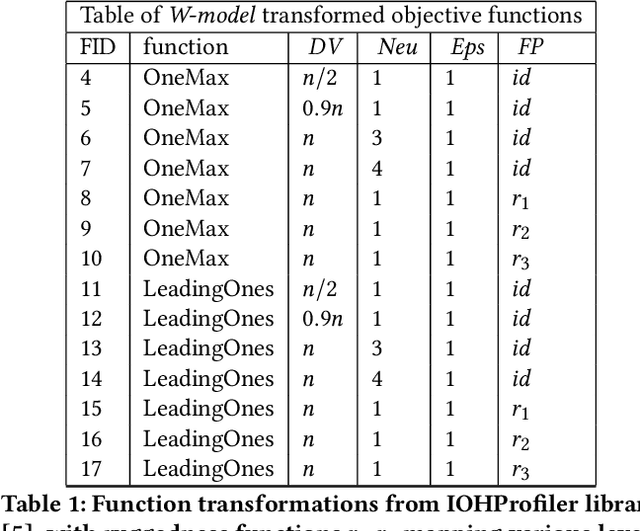
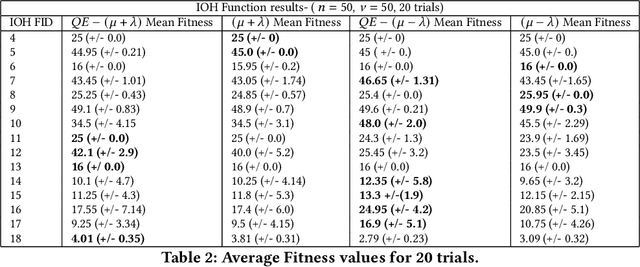
Genetic algorithms have unique properties which are useful when applied to black box optimization. Using selection, crossover, and mutation operators, candidate solutions may be obtained without the need to calculate a gradient. In this work, we study results obtained from using quantum-enhanced operators within the selection mechanism of a genetic algorithm. Our approach frames the selection process as a minimization of a binary quadratic model with which we encode fitness and distance between members of a population, and we leverage a quantum annealing system to sample low energy solutions for the selection mechanism. We benchmark these quantum-enhanced algorithms against classical algorithms over various black-box objective functions, including the OneMax function, and functions from the IOHProfiler library for black-box optimization. We observe a performance gain in average number of generations to convergence for the quantum-enhanced elitist selection operator in comparison to classical on the OneMax function. We also find that the quantum-enhanced selection operator with non-elitist selection outperform benchmarks on functions with fitness perturbation from the IOHProfiler library. Additionally, we find that in the case of elitist selection, the quantum-enhanced operators outperform classical benchmarks on functions with varying degrees of dummy variables and neutrality.

Equivariant quantum circuits for learning on weighted graphs

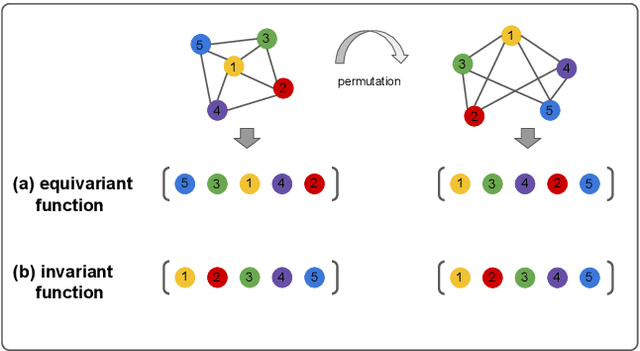
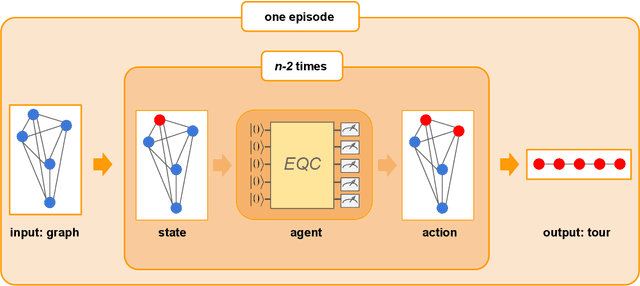
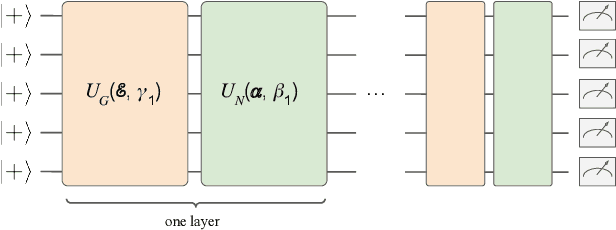
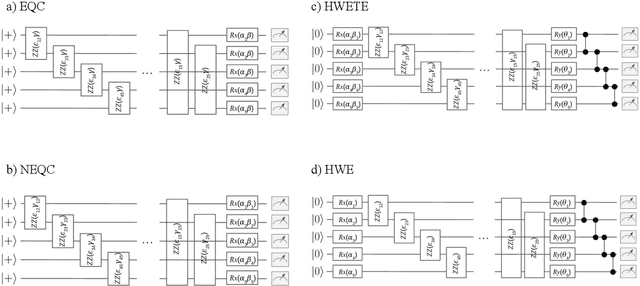
Variational quantum algorithms are the leading candidate for near-term advantage on noisy quantum hardware. When training a parametrized quantum circuit to solve a specific task, the choice of ansatz is one of the most important factors that determines the trainability and performance of the algorithm. Problem-tailored ansatzes have become the standard for tasks in optimization or quantum chemistry, and yield more efficient algorithms with better performance than unstructured approaches. In quantum machine learning (QML), however, the literature on ansatzes that are motivated by the training data structure is scarce. Considering that it is widely known that unstructured ansatzes can become untrainable with increasing system size and circuit depth, it is of key importance to also study problem-tailored circuit architectures in a QML context. In this work, we introduce an ansatz for learning tasks on weighted graphs that respects an important graph symmetry, namely equivariance under node permutations. We evaluate the performance of this ansatz on a complex learning task on weighted graphs, where a ML model is used to implement a heuristic for a combinatorial optimization problem. We analytically study the expressivity of our ansatz at depth one, and numerically compare the performance of our model on instances with up to 20 qubits to ansatzes where the equivariance property is gradually broken. We show that our ansatz outperforms all others even in the small-instance regime. Our results strengthen the notion that symmetry-preserving ansatzes are a key to success in QML and should be an active area of research in order to enable near-term advantages in this field.

Semi-supervised time series classification method for quantum computing

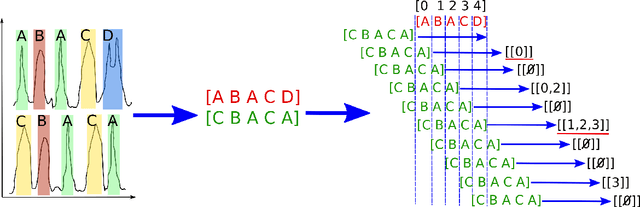
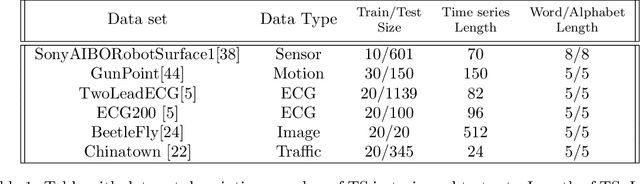
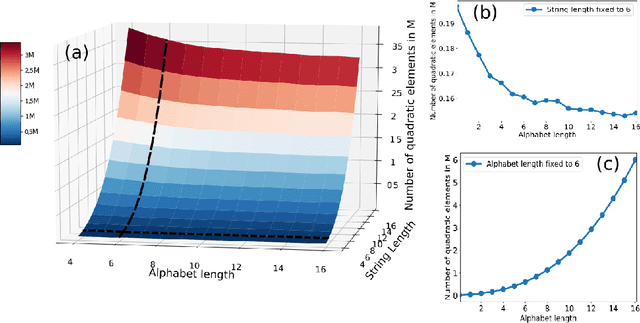
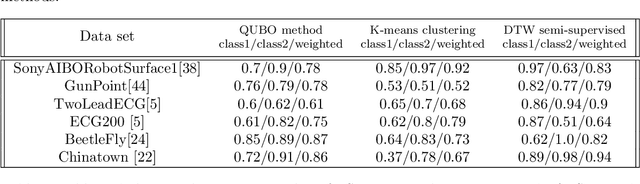
In this paper we develop methods to solve two problems related to time series (TS) analysis using quantum computing: reconstruction and classification. We formulate the task of reconstructing a given TS from a training set of data as an unconstrained binary optimization (QUBO) problem, which can be solved by both quantum annealers and gate-model quantum processors. We accomplish this by discretizing the TS and converting the reconstruction to a set cover problem, allowing us to perform a one-versus-all method of reconstruction. Using the solution to the reconstruction problem, we show how to extend this method to perform semi-supervised classification of TS data. We present results indicating our method is competitive with current semi- and unsupervised classification techniques, but using less data than classical techniques.