Quantum-Enhanced Selection Operators for Evolutionary Algorithms

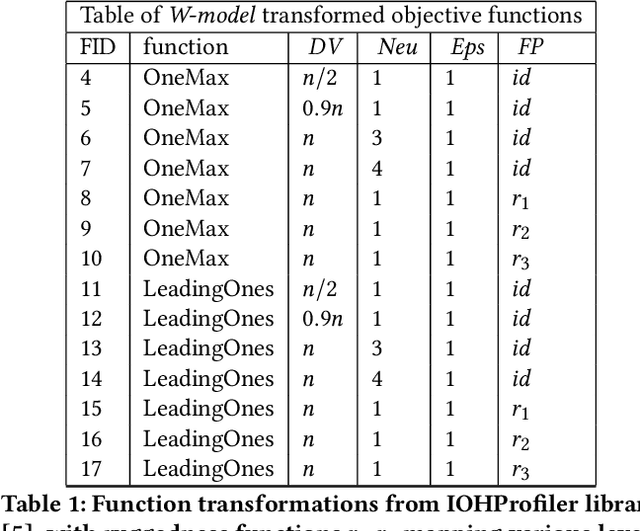
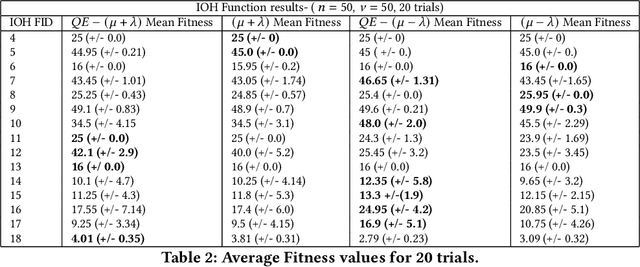
Genetic algorithms have unique properties which are useful when applied to black box optimization. Using selection, crossover, and mutation operators, candidate solutions may be obtained without the need to calculate a gradient. In this work, we study results obtained from using quantum-enhanced operators within the selection mechanism of a genetic algorithm. Our approach frames the selection process as a minimization of a binary quadratic model with which we encode fitness and distance between members of a population, and we leverage a quantum annealing system to sample low energy solutions for the selection mechanism. We benchmark these quantum-enhanced algorithms against classical algorithms over various black-box objective functions, including the OneMax function, and functions from the IOHProfiler library for black-box optimization. We observe a performance gain in average number of generations to convergence for the quantum-enhanced elitist selection operator in comparison to classical on the OneMax function. We also find that the quantum-enhanced selection operator with non-elitist selection outperform benchmarks on functions with fitness perturbation from the IOHProfiler library. Additionally, we find that in the case of elitist selection, the quantum-enhanced operators outperform classical benchmarks on functions with varying degrees of dummy variables and neutrality.

Quantum-Assisted Feature Selection for Vehicle Price Prediction Modeling

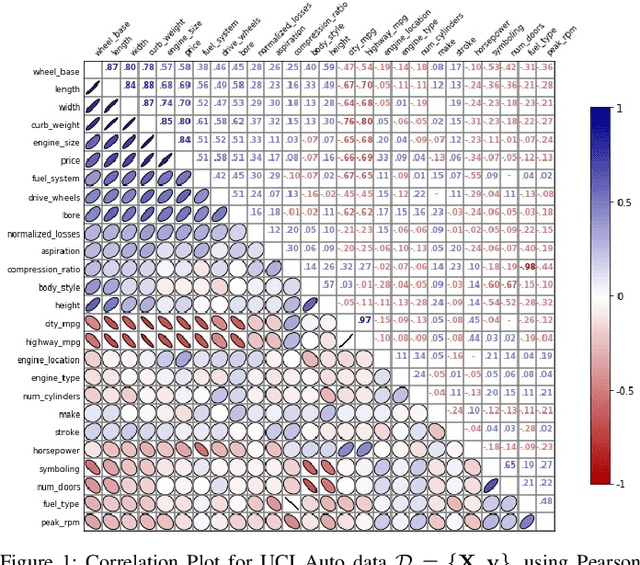
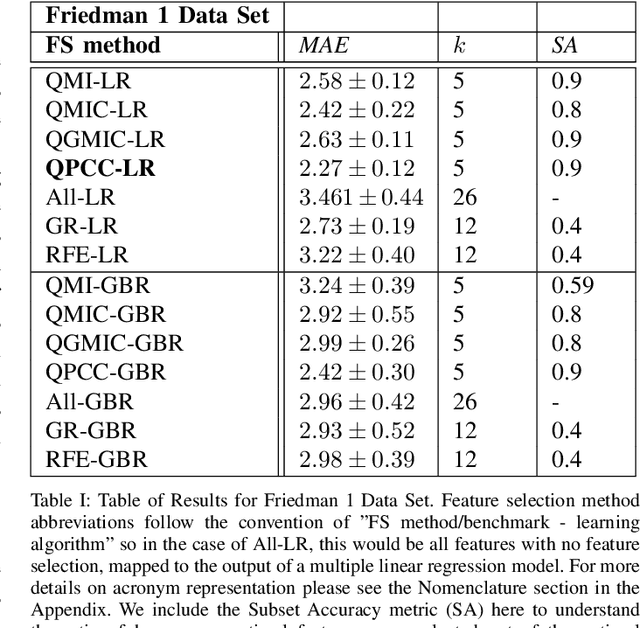
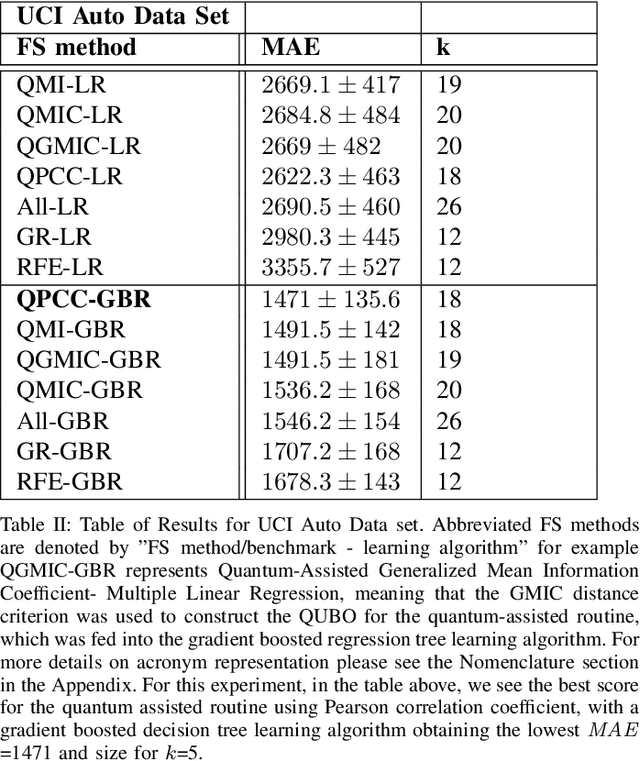
Within machine learning model evaluation regimes, feature selection is a technique to reduce model complexity and improve model performance in regards to generalization, model fit, and accuracy of prediction. However, the search over the space of features to find the subset of $k$ optimal features is a known NP-Hard problem. In this work, we study metrics for encoding the combinatorial search as a binary quadratic model, such as Generalized Mean Information Coefficient and Pearson Correlation Coefficient in application to the underlying regression problem of price prediction. We investigate trade-offs in the form of run-times and model performance, of leveraging quantum-assisted vs. classical subroutines for the combinatorial search, using minimum redundancy maximal relevancy as the heuristic for our approach. We achieve accuracy scores of 0.9 (in the range of [0,1]) for finding optimal subsets on synthetic data using a new metric that we define. We test and cross-validate predictive models on a real-world problem of price prediction, and show a performance improvement of mean absolute error scores for our quantum-assisted method $(1471.02 \pm{135.6})$, vs. similar methodologies such as recursive feature elimination $(1678.3 \pm{143.7})$. Our findings show that by leveraging quantum-assisted routines we find solutions that increase the quality of predictive model output while reducing the input dimensionality to the learning algorithm on synthetic and real-world data.

Semi-supervised time series classification method for quantum computing

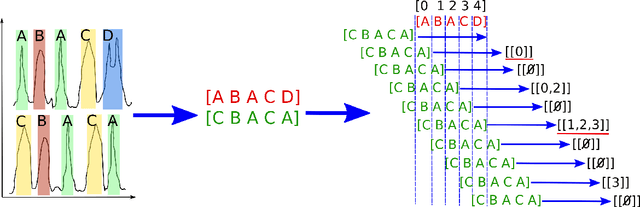
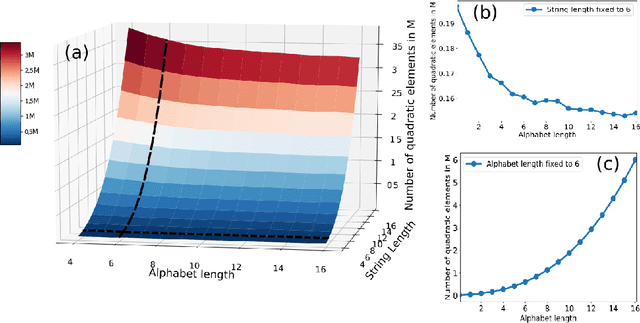
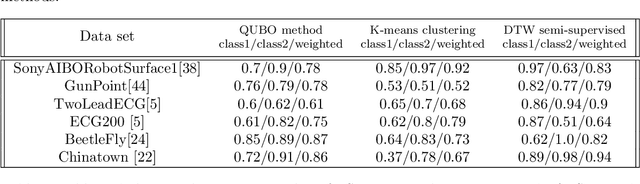
In this paper we develop methods to solve two problems related to time series (TS) analysis using quantum computing: reconstruction and classification. We formulate the task of reconstructing a given TS from a training set of data as an unconstrained binary optimization (QUBO) problem, which can be solved by both quantum annealers and gate-model quantum processors. We accomplish this by discretizing the TS and converting the reconstruction to a set cover problem, allowing us to perform a one-versus-all method of reconstruction. Using the solution to the reconstruction problem, we show how to extend this method to perform semi-supervised classification of TS data. We present results indicating our method is competitive with current semi- and unsupervised classification techniques, but using less data than classical techniques.

Artificial Intelligence and Data Science in the Automotive Industry

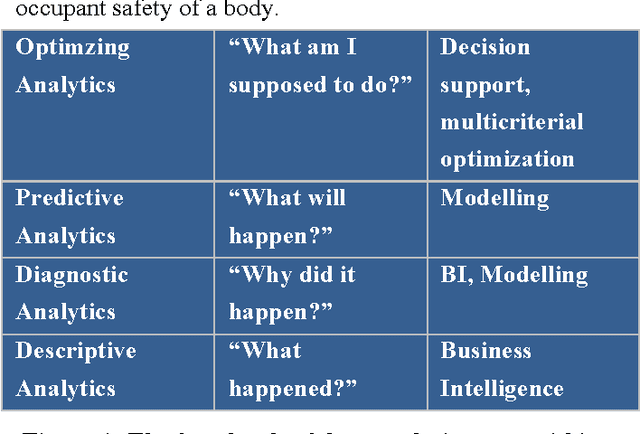
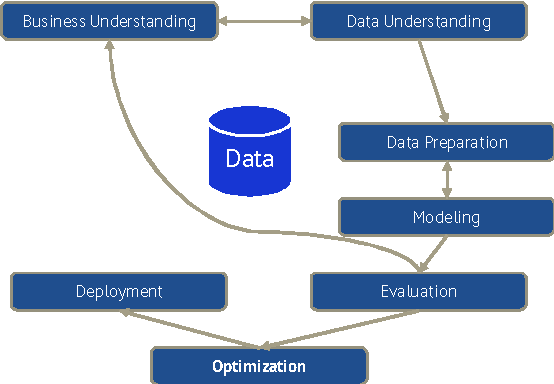
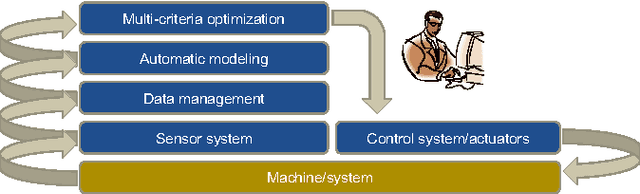
Data science and machine learning are the key technologies when it comes to the processes and products with automatic learning and optimization to be used in the automotive industry of the future. This article defines the terms "data science" (also referred to as "data analytics") and "machine learning" and how they are related. In addition, it defines the term "optimizing analytics" and illustrates the role of automatic optimization as a key technology in combination with data analytics. It also uses examples to explain the way that these technologies are currently being used in the automotive industry on the basis of the major subprocesses in the automotive value chain (development, procurement; logistics, production, marketing, sales and after-sales, connected customer). Since the industry is just starting to explore the broad range of potential uses for these technologies, visionary application examples are used to illustrate the revolutionary possibilities that they offer. Finally, the article demonstrates how these technologies can make the automotive industry more efficient and enhance its customer focus throughout all its operations and activities, extending from the product and its development process to the customers and their connection to the product.