An LLM System for Autonomous Variational Quantum Circuit Design

The design of high performing quantum circuits remains largely dependent on human expertise. We introduce an autonomous agentic framework that employs large language models (LLMs) to conduct iterative quantum circuit designs under explicit design constraints. Our system integrates seven components: Exploration, Generation, Discussion, Validation, Storage, Evaluation, and Review. These components form a closed-loop workflow that combines web-based knowledge acquisition, literature-grounded critique, executable code generation, and experimental feedback. We evaluate the framework on two tasks: quantum feature map construction for quantum machine learning and ansatz generation for variational quantum eigensolver applications in quantum chemistry. In image classification benchmarks, the best generated feature map outperforms representative quantum feature maps and, when scaled to larger qubit counts, surpasses the classical radial basis function kernel. In molecular ground state estimation across seven molecules, the generated ansatz attains competitive accuracy with widely used chemically inspired and hardware-efficient constructions while satisfying the imposed scaling constraints. These results establish LLM driven agentic system as a viable paradigm for automated quantum circuit design and illustrate how AI systems can participate in iterative scientific optimization workflows across scientific domains.

Automating quantum feature map design via large language models

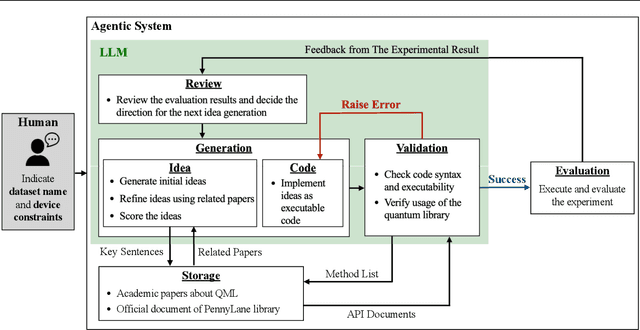
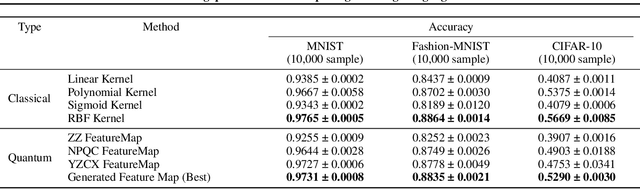
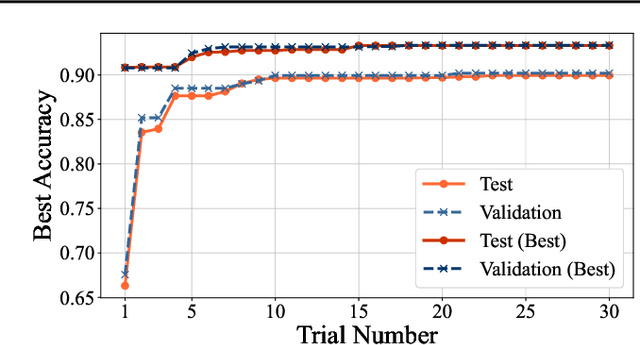
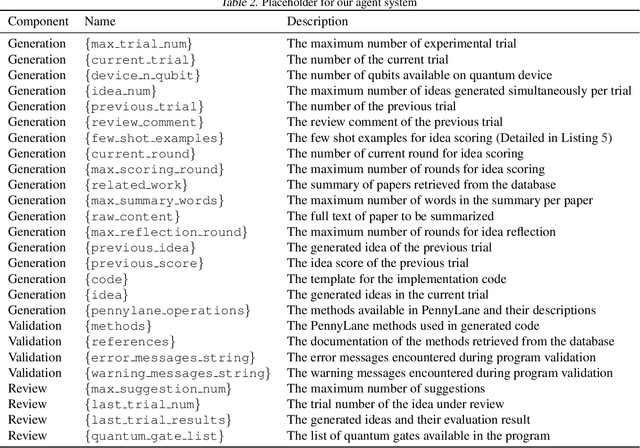
Quantum feature maps are a key component of quantum machine learning, encoding classical data into quantum states to exploit the expressive power of high-dimensional Hilbert spaces. Despite their theoretical promise, designing quantum feature maps that offer practical advantages over classical methods remains an open challenge. In this work, we propose an agentic system that autonomously generates, evaluates, and refines quantum feature maps using large language models. The system consists of five component: Generation, Storage, Validation, Evaluation, and Review. Using these components, it iteratively improves quantum feature maps. Experiments on the MNIST dataset show that it can successfully discover and refine feature maps without human intervention. The best feature map generated outperforms existing quantum baselines and achieves competitive accuracy compared to classical kernels across MNIST, Fashion-MNIST, and CIFAR-10. Our approach provides a framework for exploring dataset-adaptive quantum features and highlights the potential of LLM-driven automation in quantum algorithm design.

Quantum Kernel t-Distributed Stochastic Neighbor Embedding

Data visualization is important in understanding the characteristics of data that are difficult to see directly. It is used to visualize loss landscapes and optimization trajectories to analyze optimization performance. Popular optimization analysis is performed by visualizing a loss landscape around the reached local or global minimum using principal component analysis. However, this visualization depends on the variational parameters of a quantum circuit rather than quantum states, which makes it difficult to understand the mechanism of optimization process through the property of quantum states. Here, we propose a quantum data visualization method using quantum kernels, which enables us to offer fast and highly accurate visualization of quantum states. In our numerical experiments, we visualize hand-written digits dataset and apply $k$-nearest neighbor algorithm to the low-dimensional data to quantitatively evaluate our proposed method compared with a classical kernel method. As a result, our proposed method achieves comparable accuracy to the state-of-the-art classical kernel method, meaning that the proposed visualization method based on quantum machine learning does not degrade the separability of the input higher dimensional data. Furthermore, we visualize the optimization trajectories of finding the ground states of transverse field Ising model and successfully find the trajectory characteristics. Since quantum states are higher dimensional objects that can only be seen via observables, our visualization method, which inherits the similarity of quantum data, would be useful in understanding the behavior of quantum circuits and algorithms.

Continuous optimization by quantum adaptive distribution search

In this paper, we introduce the quantum adaptive distribution search (QuADS), a quantum continuous optimization algorithm that integrates Grover adaptive search (GAS) with the covariance matrix adaptation - evolution strategy (CMA-ES), a classical technique for continuous optimization. QuADS utilizes the quantum-based search capabilities of GAS and enhances them with the principles of CMA-ES for more efficient optimization. It employs a multivariate normal distribution for the initial state of the quantum search and repeatedly updates it throughout the optimization process. Our numerical experiments show that QuADS outperforms both GAS and CMA-ES. This is achieved through adaptive refinement of the initial state distribution rather than consistently using a uniform state, resulting in fewer oracle calls. This study presents an important step toward exploiting the potential of quantum computing for continuous optimization.

MNISQ: A Large-Scale Quantum Circuit Dataset for Machine Learning on/for Quantum Computers in the NISQ era

We introduce the first large-scale dataset, MNISQ, for both the Quantum and the Classical Machine Learning community during the Noisy Intermediate-Scale Quantum era. MNISQ consists of 4,950,000 data points organized in 9 subdatasets. Building our dataset from the quantum encoding of classical information (e.g., MNIST dataset), we deliver a dataset in a dual form: in quantum form, as circuits, and in classical form, as quantum circuit descriptions (quantum programming language, QASM). In fact, also the Machine Learning research related to quantum computers undertakes a dual challenge: enhancing machine learning exploiting the power of quantum computers, while also leveraging state-of-the-art classical machine learning methodologies to help the advancement of quantum computing. Therefore, we perform circuit classification on our dataset, tackling the task with both quantum and classical models. In the quantum endeavor, we test our circuit dataset with Quantum Kernel methods, and we show excellent results up to $97\%$ accuracy. In the classical world, the underlying quantum mechanical structures within the quantum circuit data are not trivial. Nevertheless, we test our dataset on three classical models: Structured State Space sequence model (S4), Transformer and LSTM. In particular, the S4 model applied on the tokenized QASM sequences reaches an impressive $77\%$ accuracy. These findings illustrate that quantum circuit-related datasets are likely to be quantum advantageous, but also that state-of-the-art machine learning methodologies can competently classify and recognize quantum circuits. We finally entrust the quantum and classical machine learning community the fundamental challenge to build more quantum-classical datasets like ours and to build future benchmarks from our experiments. The dataset is accessible on GitHub and its circuits are easily run in qulacs or qiskit.

The cross-sectional stock return predictions via quantum neural network and tensor network

In this paper we investigate the application of quantum and quantum-inspired machine learning algorithms to stock return predictions. Specifically, we evaluate performance of quantum neural network, an algorithm suited for noisy intermediate-scale quantum computers, and tensor network, a quantum-inspired machine learning algorithm, against classical models such as linear regression and neural networks. To evaluate their abilities, we construct portfolios based on their predictions and measure investment performances. The empirical study on the Japanese stock market shows the tensor network model achieves superior performance compared to classical benchmark models, including linear and neural network models. Though the quantum neural network model attains the lowered risk-adjusted excess return than the classical neural network models over the whole period, both the quantum neural network and tensor network models have superior performances in the latest market environment, which suggests capability of model's capturing non-linearity between input features.

Parametric t-Stochastic Neighbor Embedding With Quantum Neural Network

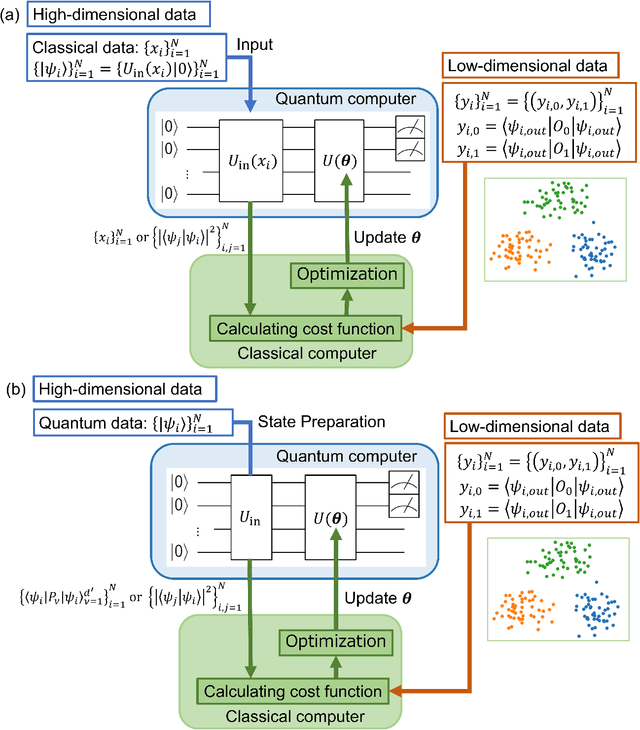
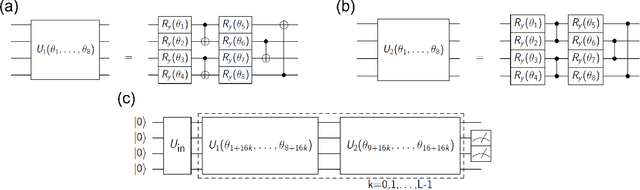
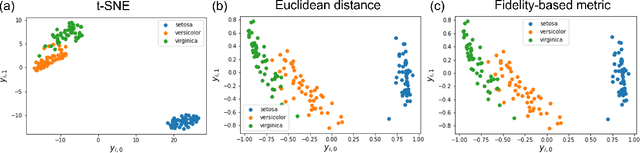
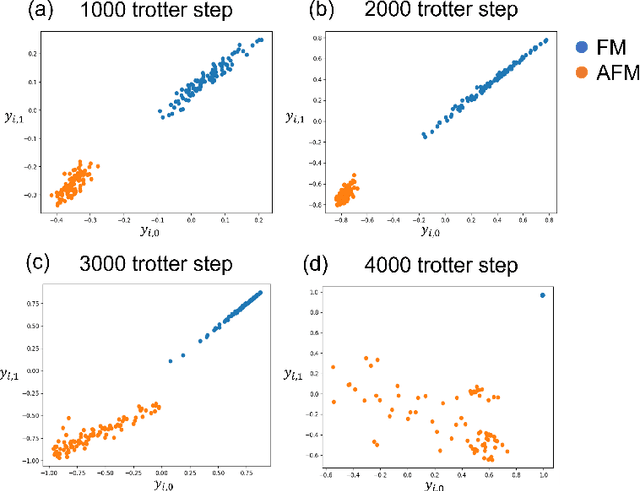
t-Stochastic Neighbor Embedding (t-SNE) is a non-parametric data visualization method in classical machine learning. It maps the data from the high-dimensional space into a low-dimensional space, especially a two-dimensional plane, while maintaining the relationship, or similarities, between the surrounding points. In t-SNE, the initial position of the low-dimensional data is randomly determined, and the visualization is achieved by moving the low-dimensional data to minimize a cost function. Its variant called parametric t-SNE uses neural networks for this mapping. In this paper, we propose to use quantum neural networks for parametric t-SNE to reflect the characteristics of high-dimensional quantum data on low-dimensional data. We use fidelity-based metrics instead of Euclidean distance in calculating high-dimensional data similarity. We visualize both classical (Iris dataset) and quantum (time-depending Hamiltonian dynamics) data for classification tasks. Since this method allows us to represent a quantum dataset in a higher dimensional Hilbert space by a quantum dataset in a lower dimension while keeping their similarity, the proposed method can also be used to compress quantum data for further quantum machine learning.

Quantum tangent kernel

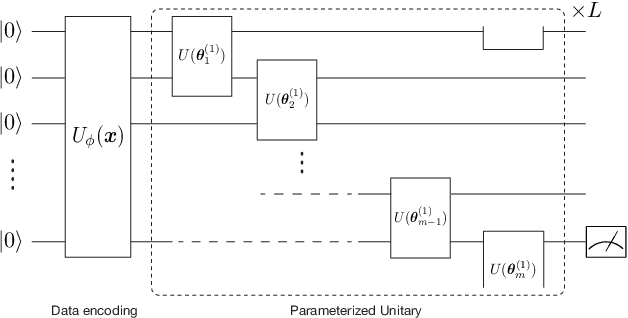
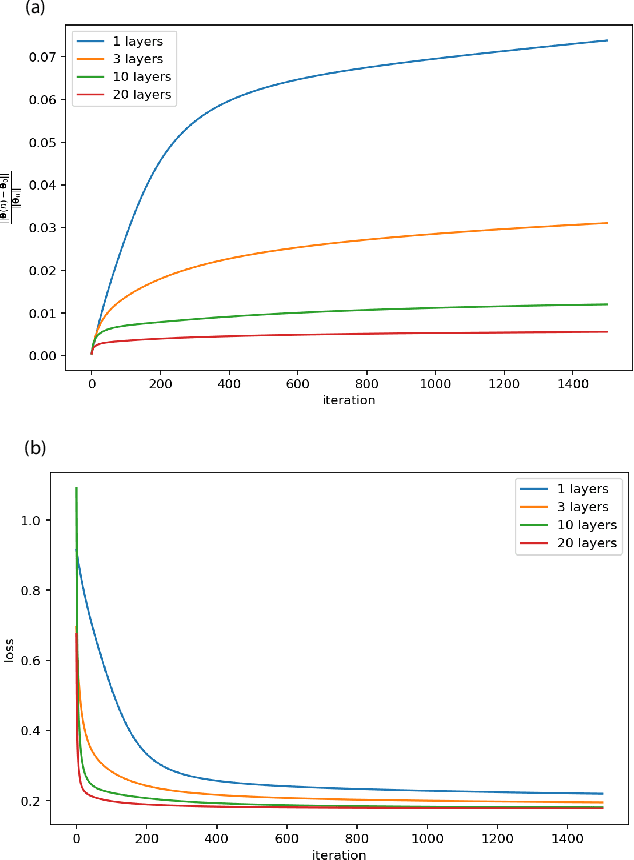
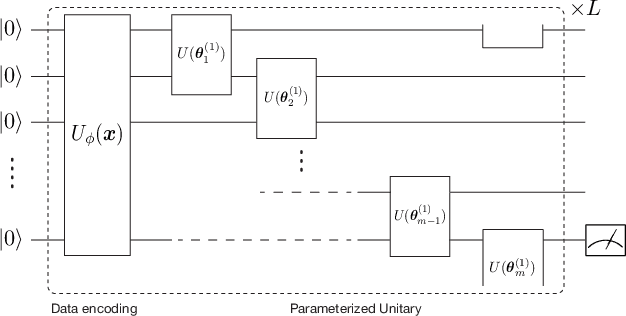
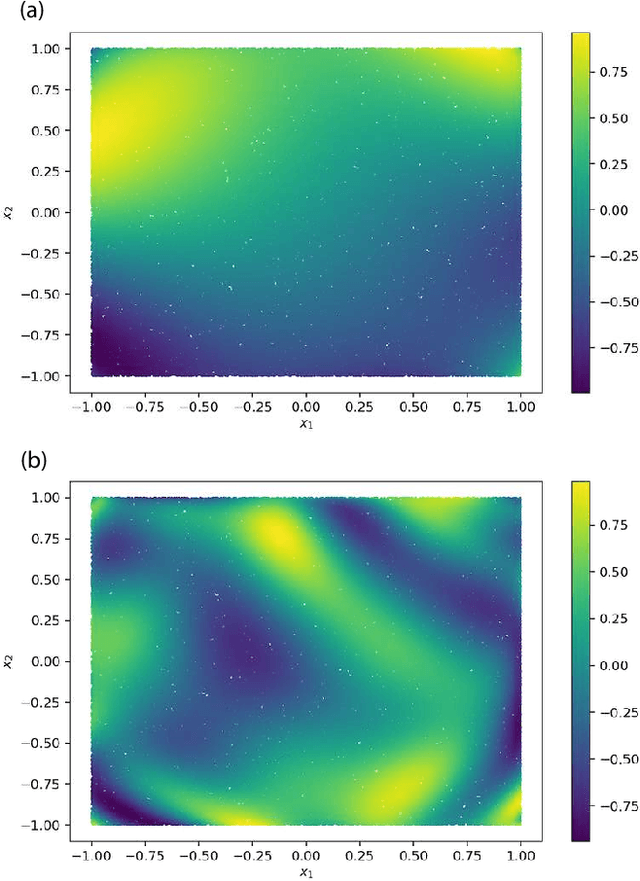
Quantum kernel method is one of the key approaches to quantum machine learning, which has the advantages that it does not require optimization and has theoretical simplicity. By virtue of these properties, several experimental demonstrations and discussions of the potential advantages have been developed so far. However, as is the case in classical machine learning, not all quantum machine learning models could be regarded as kernel methods. In this work, we explore a quantum machine learning model with a deep parameterized quantum circuit and aim to go beyond the conventional quantum kernel method. In this case, the representation power and performance are expected to be enhanced, while the training process might be a bottleneck because of the barren plateaus issue. However, we find that parameters of a deep enough quantum circuit do not move much from its initial values during training, allowing first-order expansion with respect to the parameters. This behavior is similar to the neural tangent kernel in the classical literatures, and such a deep variational quantum machine learning can be described by another emergent kernel, quantum tangent kernel. Numerical simulations show that the proposed quantum tangent kernel outperforms the conventional quantum kernel method for an ansatz-generated dataset. This work provides a new direction beyond the conventional quantum kernel method and explores potential power of quantum machine learning with deep parameterized quantum circuits.

Variational Quantum Algorithms

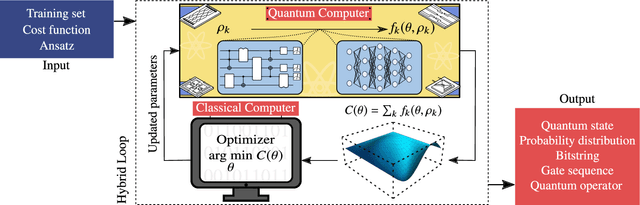
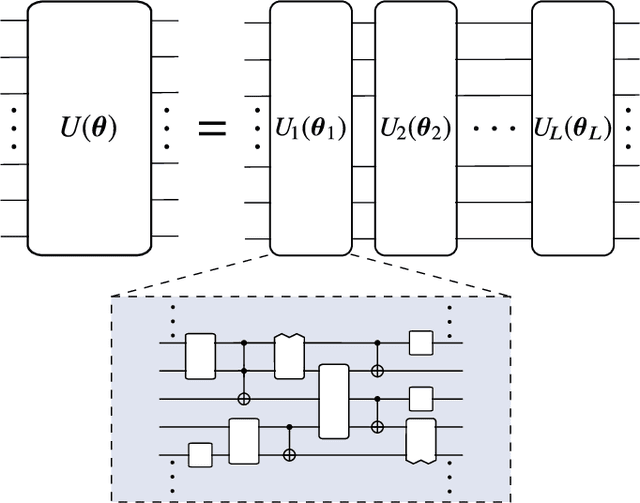
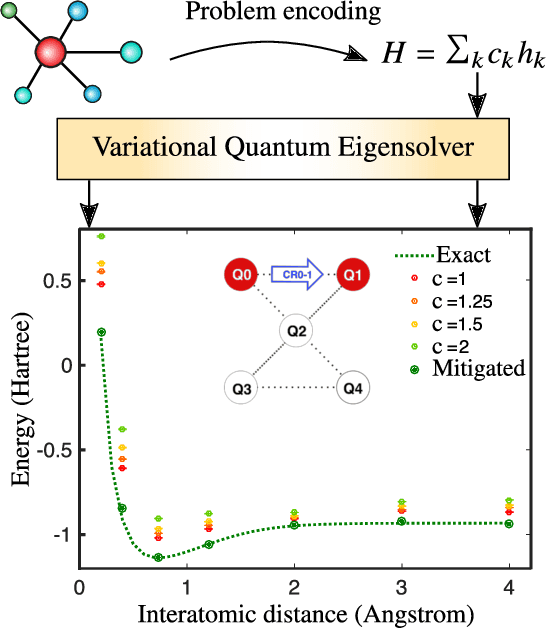
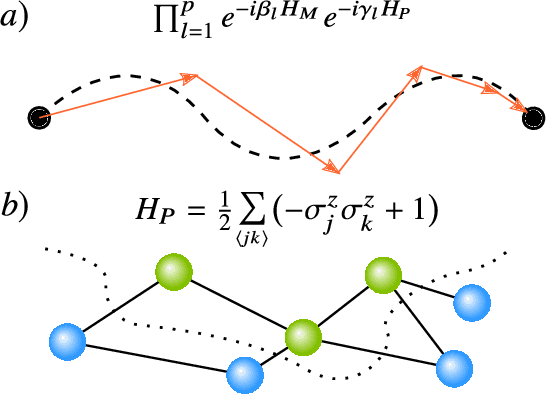
Applications such as simulating large quantum systems or solving large-scale linear algebra problems are immensely challenging for classical computers due their extremely high computational cost. Quantum computers promise to unlock these applications, although fault-tolerant quantum computers will likely not be available for several years. Currently available quantum devices have serious constraints, including limited qubit numbers and noise processes that limit circuit depth. Variational Quantum Algorithms (VQAs), which employ a classical optimizer to train a parametrized quantum circuit, have emerged as a leading strategy to address these constraints. VQAs have now been proposed for essentially all applications that researchers have envisioned for quantum computers, and they appear to the best hope for obtaining quantum advantage. Nevertheless, challenges remain including the trainability, accuracy, and efficiency of VQAs. In this review article we present an overview of the field of VQAs. Furthermore, we discuss strategies to overcome their challenges as well as the exciting prospects for using them as a means to obtain quantum advantage.