Entangled Datasets for Quantum Machine Learning

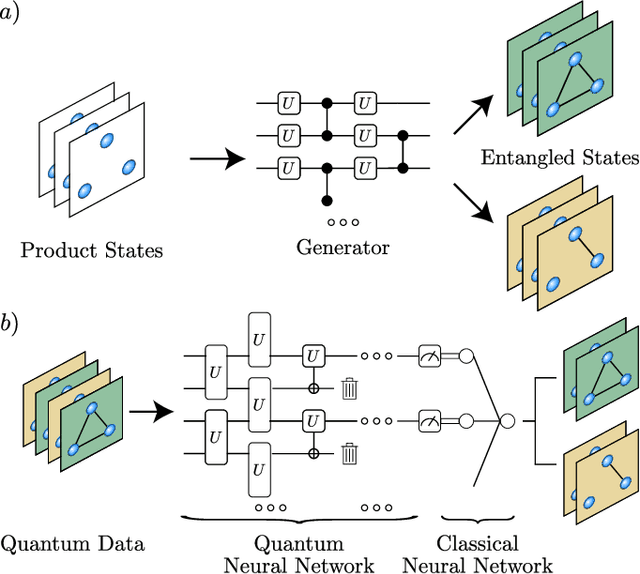
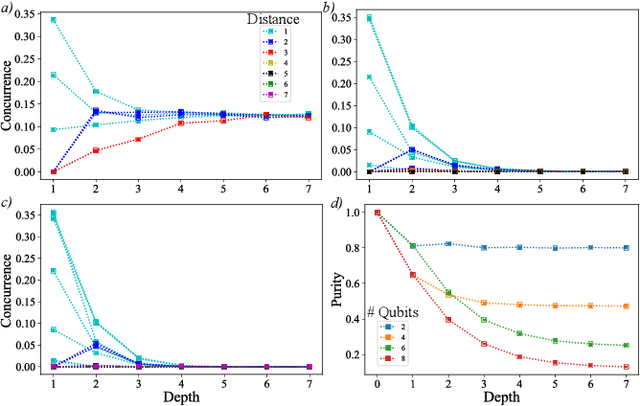
High-quality, large-scale datasets have played a crucial role in the development and success of classical machine learning. Quantum Machine Learning (QML) is a new field that aims to use quantum computers for data analysis, with the hope of obtaining a quantum advantage of some sort. While most proposed QML architectures are benchmarked using classical datasets, there is still doubt whether QML on classical datasets will achieve such an advantage. In this work, we argue that one should instead employ quantum datasets composed of quantum states. For this purpose, we introduce the NTangled dataset composed of quantum states with different amounts and types of multipartite entanglement. We first show how a quantum neural network can be trained to generate the states in the NTangled dataset. Then, we use the NTangled dataset to benchmark QML models for supervised learning classification tasks. We also consider an alternative entanglement-based dataset, which is scalable and is composed of states prepared by quantum circuits with different depths. As a byproduct of our results, we introduce a novel method for generating multipartite entangled states, providing a use-case of quantum neural networks for quantum entanglement theory.

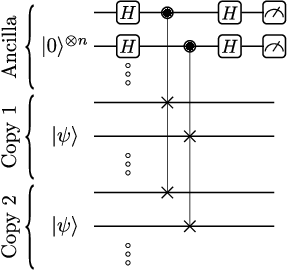
Can Error Mitigation Improve Trainability of Noisy Variational Quantum Algorithms?

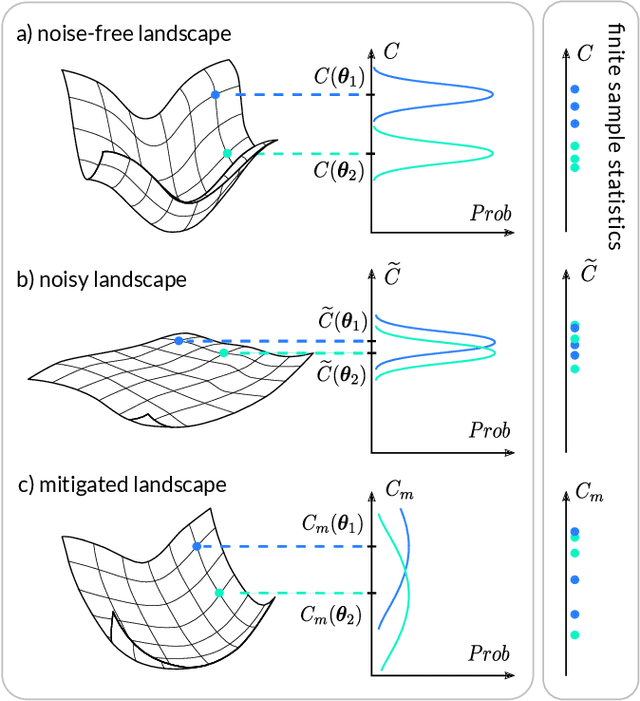
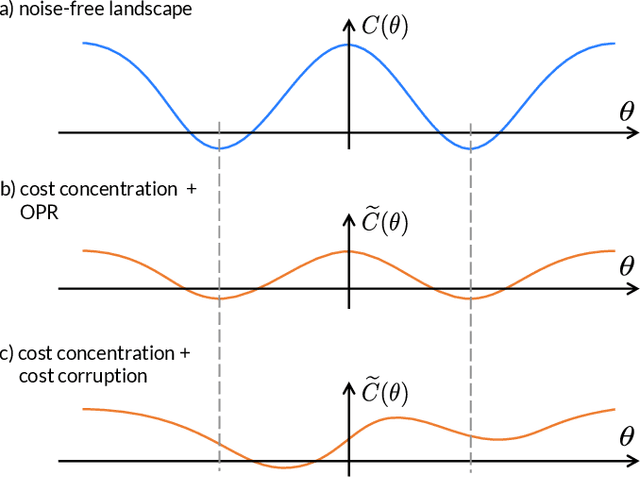
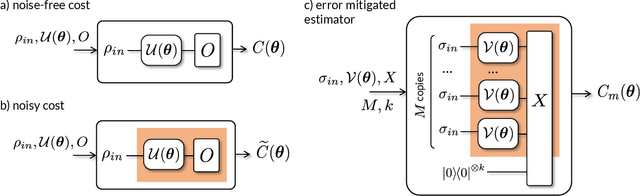
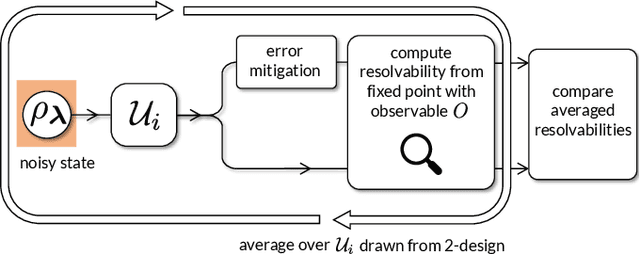
Variational Quantum Algorithms (VQAs) are widely viewed as the best hope for near-term quantum advantage. However, recent studies have shown that noise can severely limit the trainability of VQAs, e.g., by exponentially flattening the cost landscape and suppressing the magnitudes of cost gradients. Error Mitigation (EM) shows promise in reducing the impact of noise on near-term devices. Thus, it is natural to ask whether EM can improve the trainability of VQAs. In this work, we first show that, for a broad class of EM strategies, exponential cost concentration cannot be resolved without committing exponential resources elsewhere. This class of strategies includes as special cases Zero Noise Extrapolation, Virtual Distillation, Probabilistic Error Cancellation, and Clifford Data Regression. Second, we perform analytical and numerical analysis of these EM protocols, and we find that some of them (e.g., Virtual Distillation) can make it harder to resolve cost function values compared to running no EM at all. As a positive result, we do find numerical evidence that Clifford Data Regression (CDR) can aid the training process in certain settings where cost concentration is not too severe. Our results show that care should be taken in applying EM protocols as they can either worsen or not improve trainability. On the other hand, our positive results for CDR highlight the possibility of engineering error mitigation methods to improve trainability.

Adaptive shot allocation for fast convergence in variational quantum algorithms

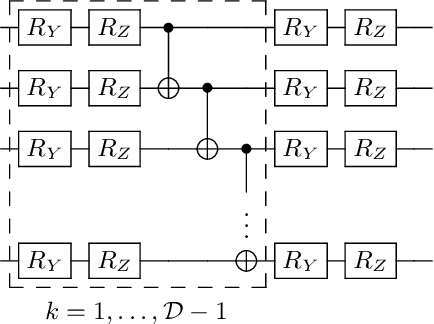
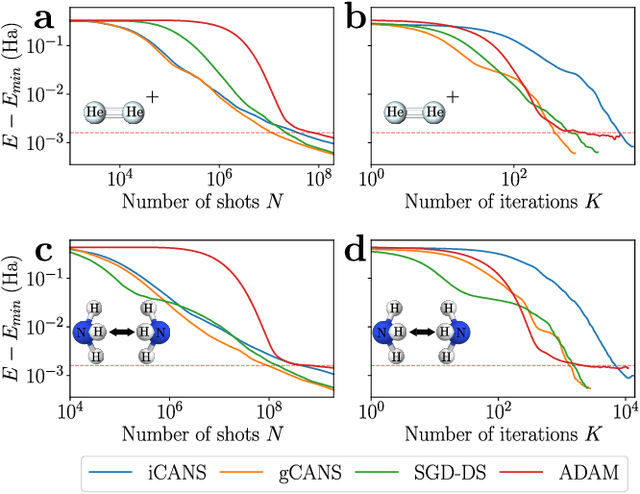
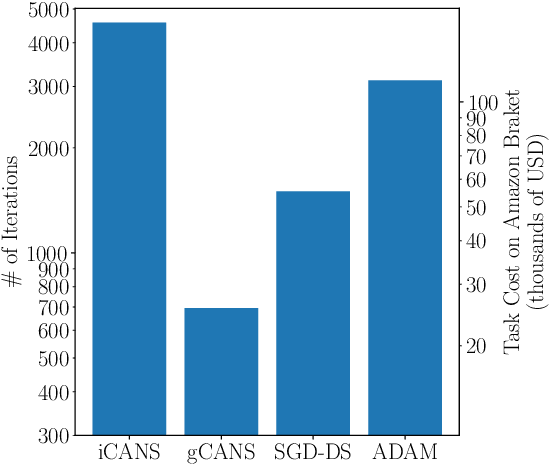
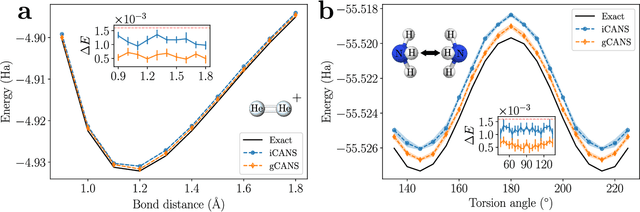
Variational Quantum Algorithms (VQAs) are a promising approach for practical applications like chemistry and materials science on near-term quantum computers as they typically reduce quantum resource requirements. However, in order to implement VQAs, an efficient classical optimization strategy is required. Here we present a new stochastic gradient descent method using an adaptive number of shots at each step, called the global Coupled Adaptive Number of Shots (gCANS) method, which improves on prior art in both the number of iterations as well as the number of shots required. These improvements reduce both the time and money required to run VQAs on current cloud platforms. We analytically prove that in a convex setting gCANS achieves geometric convergence to the optimum. Further, we numerically investigate the performance of gCANS on some chemical configuration problems. We also consider finding the ground state for an Ising model with different numbers of spins to examine the scaling of the method. We find that for these problems, gCANS compares favorably to all of the other optimizers we consider.

Equivalence of quantum barren plateaus to cost concentration and narrow gorges

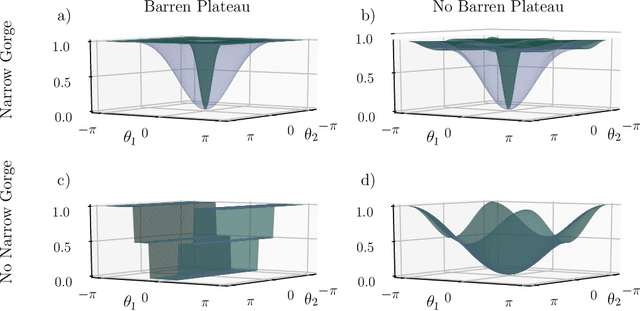
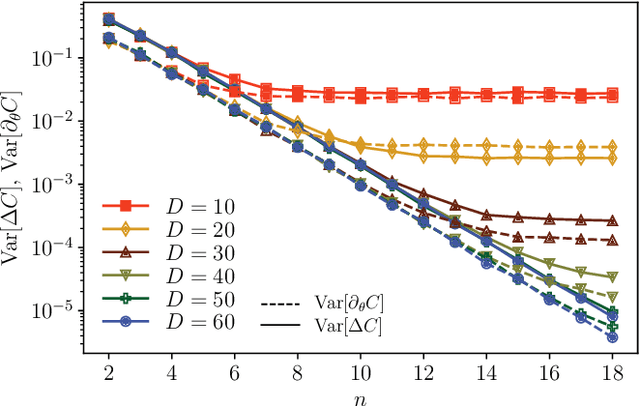
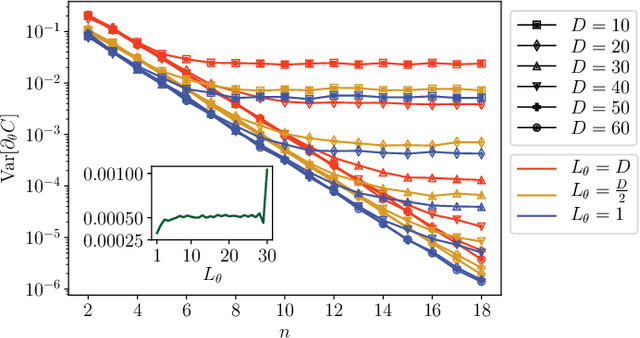
Optimizing parameterized quantum circuits (PQCs) is the leading approach to make use of near-term quantum computers. However, very little is known about the cost function landscape for PQCs, which hinders progress towards quantum-aware optimizers. In this work, we investigate the connection between three different landscape features that have been observed for PQCs: (1) exponentially vanishing gradients (called barren plateaus), (2) exponential cost concentration about the mean, and (3) the exponential narrowness of minina (called narrow gorges). We analytically prove that these three phenomena occur together, i.e., when one occurs then so do the other two. A key implication of this result is that one can numerically diagnose barren plateaus via cost differences rather than via the computationally more expensive gradients. More broadly, our work shows that quantum mechanics rules out certain cost landscapes (which otherwise would be mathematically possible), and hence our results are interesting from a quantum foundations perspective.

Long-time simulations with high fidelity on quantum hardware

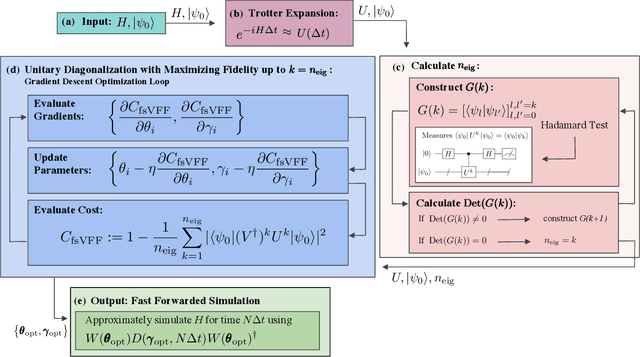
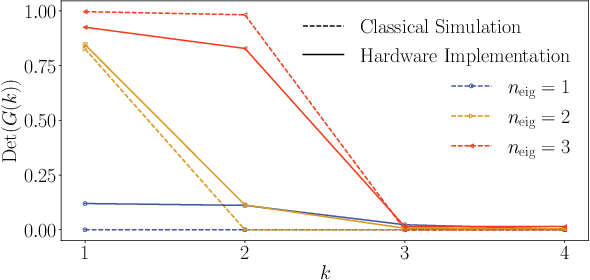
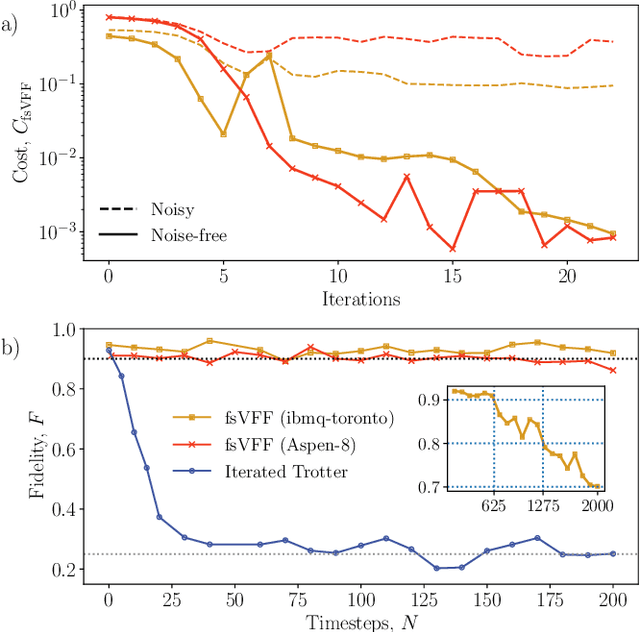
Moderate-size quantum computers are now publicly accessible over the cloud, opening the exciting possibility of performing dynamical simulations of quantum systems. However, while rapidly improving, these devices have short coherence times, limiting the depth of algorithms that may be successfully implemented. Here we demonstrate that, despite these limitations, it is possible to implement long-time, high fidelity simulations on current hardware. Specifically, we simulate an XY-model spin chain on the Rigetti and IBM quantum computers, maintaining a fidelity of at least 0.9 for over 600 time steps. This is a factor of 150 longer than is possible using the iterated Trotter method. Our simulations are performed using a new algorithm that we call the fixed state Variational Fast Forwarding (fsVFF) algorithm. This algorithm decreases the circuit depth and width required for a quantum simulation by finding an approximate diagonalization of a short time evolution unitary. Crucially, fsVFF only requires finding a diagonalization on the subspace spanned by the initial state, rather than on the total Hilbert space as with previous methods, substantially reducing the required resources.

Variational Quantum Algorithms

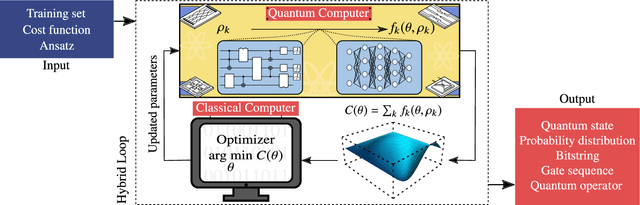
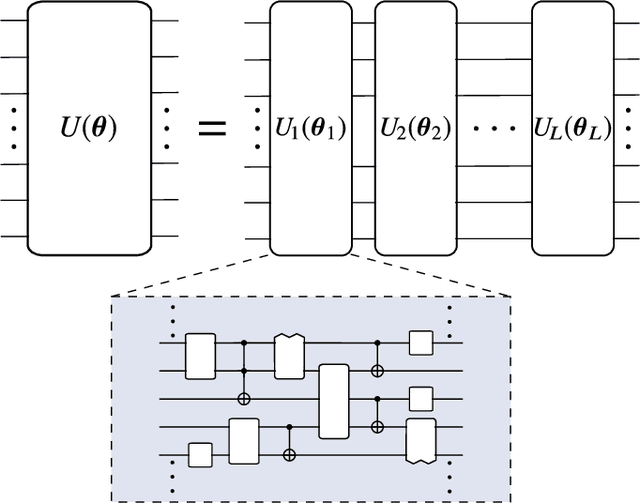
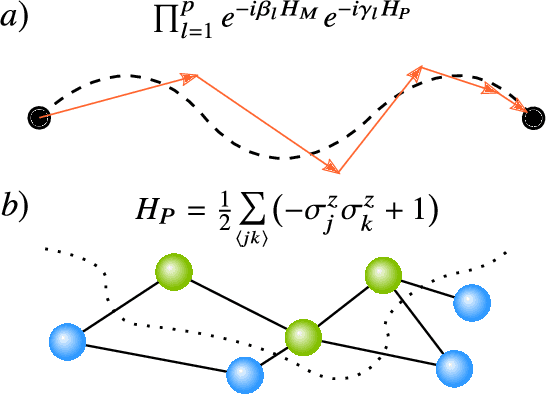
Applications such as simulating large quantum systems or solving large-scale linear algebra problems are immensely challenging for classical computers due their extremely high computational cost. Quantum computers promise to unlock these applications, although fault-tolerant quantum computers will likely not be available for several years. Currently available quantum devices have serious constraints, including limited qubit numbers and noise processes that limit circuit depth. Variational Quantum Algorithms (VQAs), which employ a classical optimizer to train a parametrized quantum circuit, have emerged as a leading strategy to address these constraints. VQAs have now been proposed for essentially all applications that researchers have envisioned for quantum computers, and they appear to the best hope for obtaining quantum advantage. Nevertheless, challenges remain including the trainability, accuracy, and efficiency of VQAs. In this review article we present an overview of the field of VQAs. Furthermore, we discuss strategies to overcome their challenges as well as the exciting prospects for using them as a means to obtain quantum advantage.

Effect of barren plateaus on gradient-free optimization

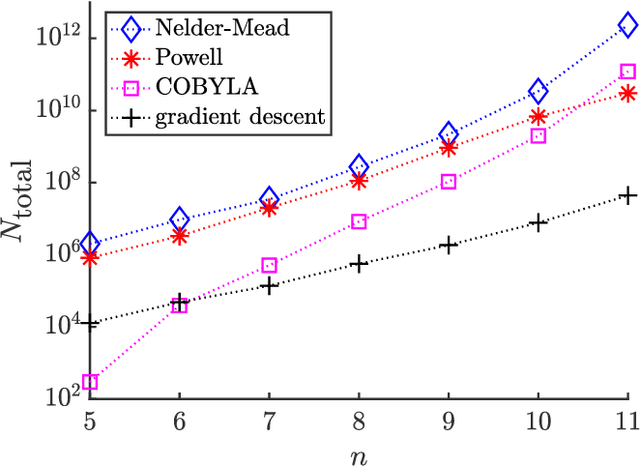
Barren plateau landscapes correspond to gradients that vanish exponentially in the number of qubits. Such landscapes have been demonstrated for variational quantum algorithms and quantum neural networks with either deep circuits or global cost functions. For obvious reasons, it is expected that gradient-based optimizers will be significantly affected by barren plateaus. However, whether or not gradient-free optimizers are impacted is a topic of debate, with some arguing that gradient-free approaches are unaffected by barren plateaus. Here we show that, indeed, gradient-free optimizers do not solve the barren plateau problem. Our main result proves that cost function differences, which are the basis for making decisions in a gradient-free optimization, are exponentially suppressed in a barren plateau. Hence, without exponential precision, gradient-free optimizers will not make progress in the optimization. We numerically confirm this by training in a barren plateau with several gradient-free optimizers (Nelder-Mead, Powell, and COBYLA algorithms), and show that the numbers of shots required in the optimization grows exponentially with the number of qubits.

Optimizing parametrized quantum circuits via noise-induced breaking of symmetries

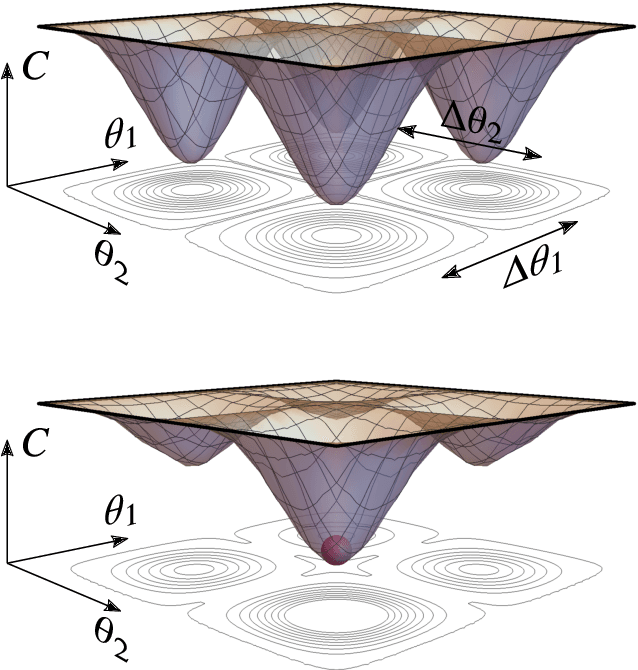
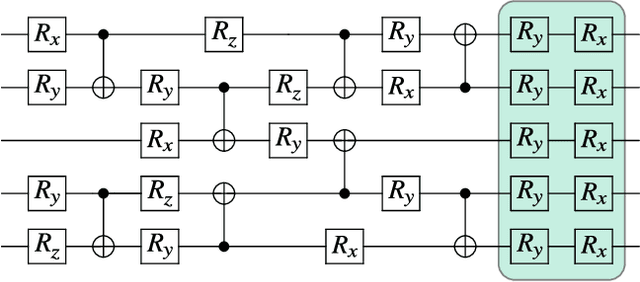
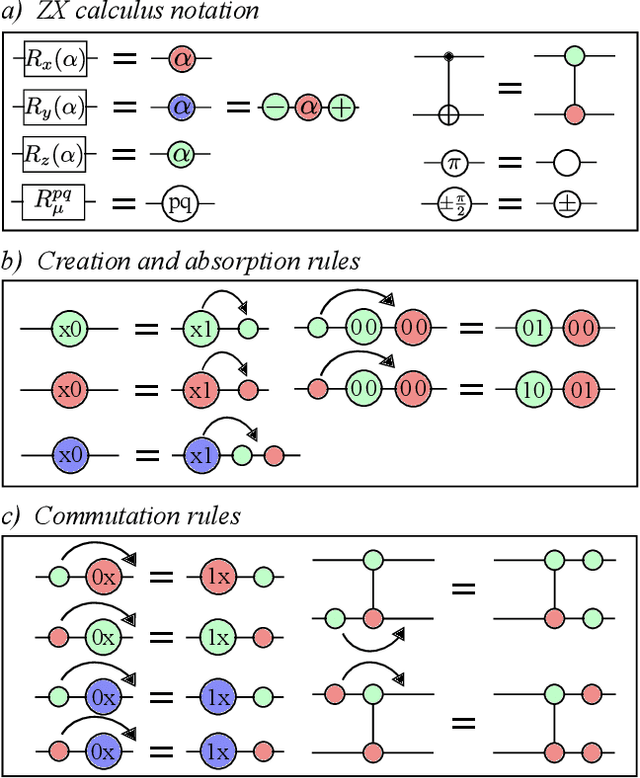
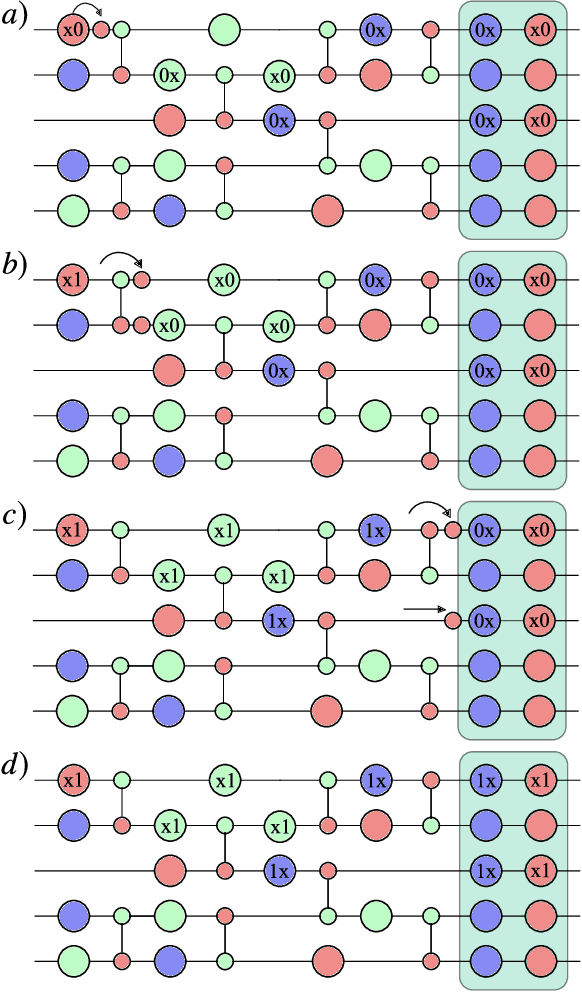
Very little is known about the cost landscape for parametrized Quantum Circuits (PQCs). Nevertheless, PQCs are employed in Quantum Neural Networks and Variational Quantum Algorithms, which may allow for near-term quantum advantage. Such applications require good optimizers to train PQCs. Recent works have focused on quantum-aware optimizers specifically tailored for PQCs. However, ignorance of the cost landscape could hinder progress towards such optimizers. In this work, we analytically prove two results for PQCs: (1) We find an exponentially large symmetry in PQCs, yielding an exponentially large degeneracy of the minima in the cost landscape. (2) We show that noise (specifically non-unital noise) can break these symmetries and lift the degeneracy of minima, making many of them local minima instead of global minima. Based on these results, we introduce an optimization method called Symmetry-based Minima Hopping (SYMH), which exploits the underlying symmetries in PQCs to hop between local minima in the cost landscape. The versatility of SYMH allows it to be combined with local optimizers (e.g., gradient descent) with minimal overhead. Our numerical simulations show that SYMH improves the overall optimizer performance.