Demonstration of Robust and Efficient Quantum Property Learning with Shallow Shadows

Extracting information efficiently from quantum systems is a major component of quantum information processing tasks. Randomized measurements, or classical shadows, enable predicting many properties of arbitrary quantum states using few measurements. While random single qubit measurements are experimentally friendly and suitable for learning low-weight Pauli observables, they perform poorly for nonlocal observables. Prepending a shallow random quantum circuit before measurements maintains this experimental friendliness, but also has favorable sample complexities for observables beyond low-weight Paulis, including high-weight Paulis and global low-rank properties such as fidelity. However, in realistic scenarios, quantum noise accumulated with each additional layer of the shallow circuit biases the results. To address these challenges, we propose the robust shallow shadows protocol. Our protocol uses Bayesian inference to learn the experimentally relevant noise model and mitigate it in postprocessing. This mitigation introduces a bias-variance trade-off: correcting for noise-induced bias comes at the cost of a larger estimator variance. Despite this increased variance, as we demonstrate on a superconducting quantum processor, our protocol correctly recovers state properties such as expectation values, fidelity, and entanglement entropy, while maintaining a lower sample complexity compared to the random single qubit measurement scheme. We also theoretically analyze the effects of noise on sample complexity and show how the optimal choice of the shallow shadow depth varies with noise strength. This combined theoretical and experimental analysis positions the robust shallow shadow protocol as a scalable, robust, and sample-efficient protocol for characterizing quantum states on current quantum computing platforms.

Exploiting Inductive Biases in Video Modeling through Neural CDEs

We introduce a novel approach to video modeling that leverages controlled differential equations (CDEs) to address key challenges in video tasks, notably video interpolation and mask propagation. We apply CDEs at varying resolutions leading to a continuous-time U-Net architecture. Unlike traditional methods, our approach does not require explicit optical flow learning, and instead makes use of the inherent continuous-time features of CDEs to produce a highly expressive video model. We demonstrate competitive performance against state-of-the-art models for video interpolation and mask propagation tasks.

Variable Length Embeddings

In this work, we introduce a novel deep learning architecture, Variable Length Embeddings (VLEs), an autoregressive model that can produce a latent representation composed of an arbitrary number of tokens. As a proof of concept, we demonstrate the capabilities of VLEs on tasks that involve reconstruction and image decomposition. We evaluate our experiments on a mix of the iNaturalist and ImageNet datasets and find that VLEs achieve comparable reconstruction results to a state of the art VAE, using less than a tenth of the parameters.

Practical Black Box Hamiltonian Learning

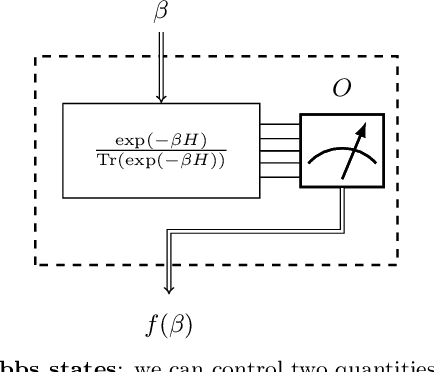
We study the problem of learning the parameters for the Hamiltonian of a quantum many-body system, given limited access to the system. In this work, we build upon recent approaches to Hamiltonian learning via derivative estimation. We propose a protocol that improves the scaling dependence of prior works, particularly with respect to parameters relating to the structure of the Hamiltonian (e.g., its locality $k$). Furthermore, by deriving exact bounds on the performance of our protocol, we are able to provide a precise numerical prescription for theoretically optimal settings of hyperparameters in our learning protocol, such as the maximum evolution time (when learning with unitary dynamics) or minimum temperature (when learning with Gibbs states). Thanks to these improvements, our protocol is practical for large problems: we demonstrate this with a numerical simulation of our protocol on an 80-qubit system.

Adaptive shot allocation for fast convergence in variational quantum algorithms

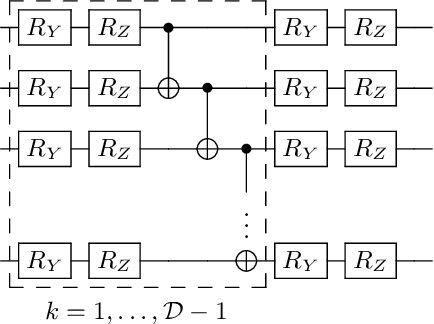
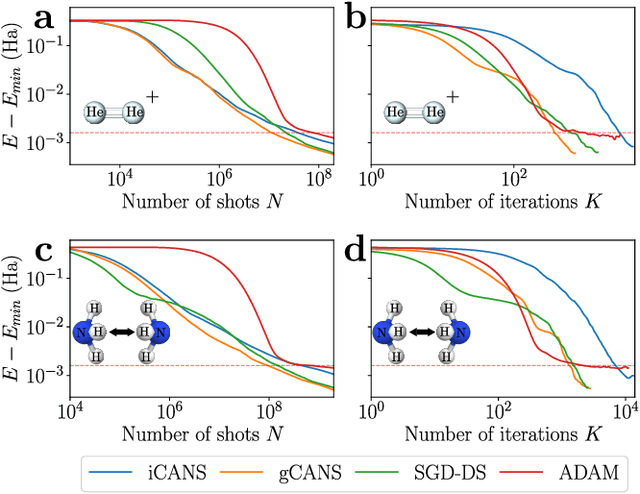
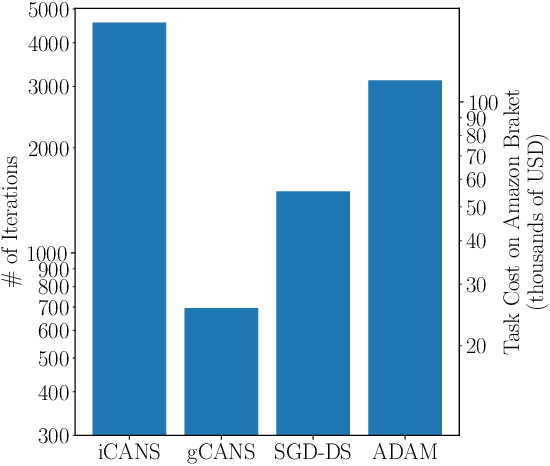
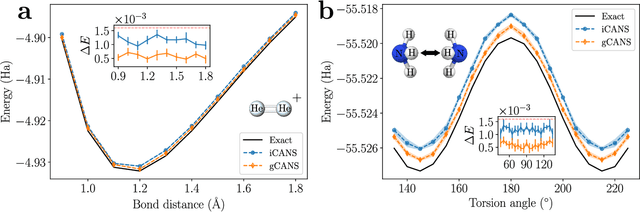
Variational Quantum Algorithms (VQAs) are a promising approach for practical applications like chemistry and materials science on near-term quantum computers as they typically reduce quantum resource requirements. However, in order to implement VQAs, an efficient classical optimization strategy is required. Here we present a new stochastic gradient descent method using an adaptive number of shots at each step, called the global Coupled Adaptive Number of Shots (gCANS) method, which improves on prior art in both the number of iterations as well as the number of shots required. These improvements reduce both the time and money required to run VQAs on current cloud platforms. We analytically prove that in a convex setting gCANS achieves geometric convergence to the optimum. Further, we numerically investigate the performance of gCANS on some chemical configuration problems. We also consider finding the ground state for an Ising model with different numbers of spins to examine the scaling of the method. We find that for these problems, gCANS compares favorably to all of the other optimizers we consider.