Demonstration of Robust and Efficient Quantum Property Learning with Shallow Shadows

Extracting information efficiently from quantum systems is a major component of quantum information processing tasks. Randomized measurements, or classical shadows, enable predicting many properties of arbitrary quantum states using few measurements. While random single qubit measurements are experimentally friendly and suitable for learning low-weight Pauli observables, they perform poorly for nonlocal observables. Prepending a shallow random quantum circuit before measurements maintains this experimental friendliness, but also has favorable sample complexities for observables beyond low-weight Paulis, including high-weight Paulis and global low-rank properties such as fidelity. However, in realistic scenarios, quantum noise accumulated with each additional layer of the shallow circuit biases the results. To address these challenges, we propose the robust shallow shadows protocol. Our protocol uses Bayesian inference to learn the experimentally relevant noise model and mitigate it in postprocessing. This mitigation introduces a bias-variance trade-off: correcting for noise-induced bias comes at the cost of a larger estimator variance. Despite this increased variance, as we demonstrate on a superconducting quantum processor, our protocol correctly recovers state properties such as expectation values, fidelity, and entanglement entropy, while maintaining a lower sample complexity compared to the random single qubit measurement scheme. We also theoretically analyze the effects of noise on sample complexity and show how the optimal choice of the shallow shadow depth varies with noise strength. This combined theoretical and experimental analysis positions the robust shallow shadow protocol as a scalable, robust, and sample-efficient protocol for characterizing quantum states on current quantum computing platforms.

Digital-analog quantum learning on Rydberg atom arrays

We propose hybrid digital-analog learning algorithms on Rydberg atom arrays, combining the potentially practical utility and near-term realizability of quantum learning with the rapidly scaling architectures of neutral atoms. Our construction requires only single-qubit operations in the digital setting and global driving according to the Rydberg Hamiltonian in the analog setting. We perform a comprehensive numerical study of our algorithm on both classical and quantum data, given respectively by handwritten digit classification and unsupervised quantum phase boundary learning. We show in the two representative problems that digital-analog learning is not only feasible in the near term, but also requires shorter circuit depths and is more robust to realistic error models as compared to digital learning schemes. Our results suggest that digital-analog learning opens a promising path towards improved variational quantum learning experiments in the near term.

Many-body localized hidden Born machine

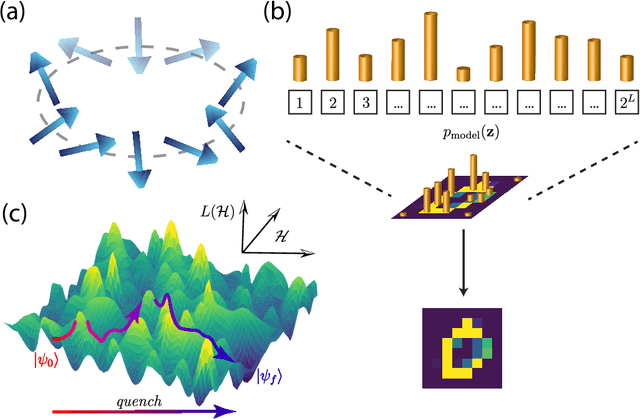
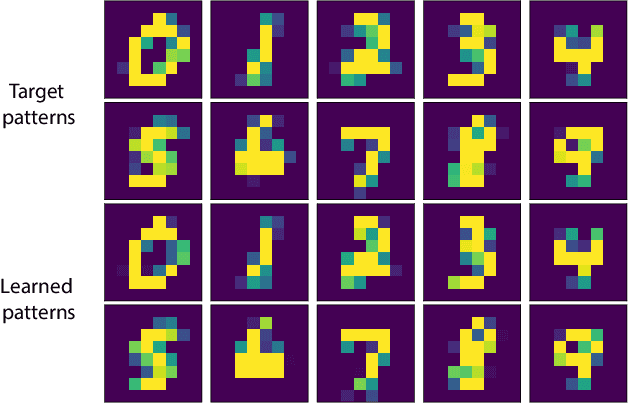
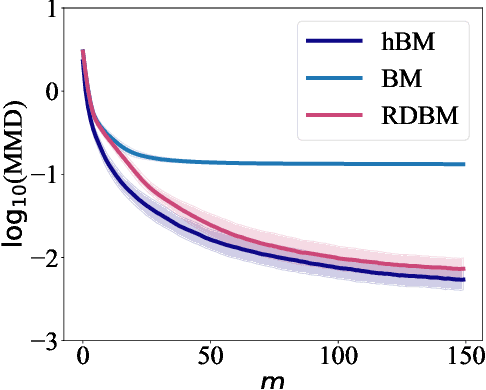
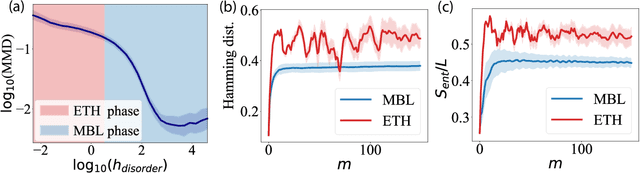
Born Machines are quantum-inspired generative models that leverage the probabilistic nature of quantum states. Here, we present a new architecture called many-body localized (MBL) hidden Born machine that uses both MBL dynamics and hidden units as learning resources. We theoretically prove that MBL Born machines possess more expressive power than classical models, and the introduction of hidden units boosts its learning power. We numerically demonstrate that the MBL hidden Born machine is capable of learning a toy dataset consisting of patterns of MNIST handwritten digits, quantum data obtained from quantum many-body states, and non-local parity data. In order to understand the mechanism behind learning, we track physical quantities such as von Neumann entanglement entropy and Hamming distance during learning, and compare the learning outcomes in the MBL, thermal, and Anderson localized phases. We show that the superior learning power of the MBL phase relies importantly on both localization and interaction. Our architecture and algorithm provide novel strategies of utilizing quantum many-body systems as learning resources, and reveal a powerful connection between disorder, interaction, and learning in quantum systems.

Learning quantum symmetries with interactive quantum-classical variational algorithms

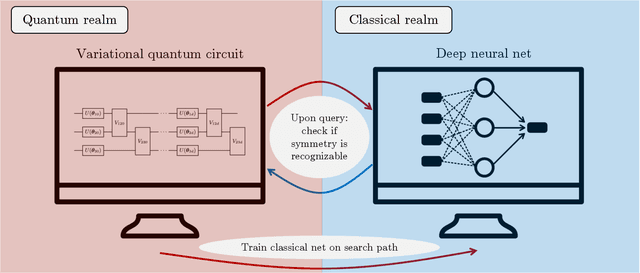
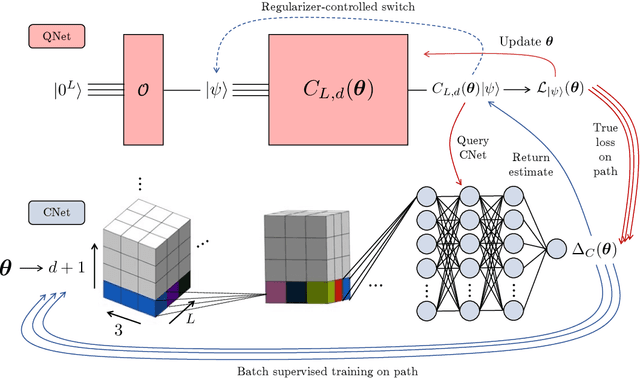
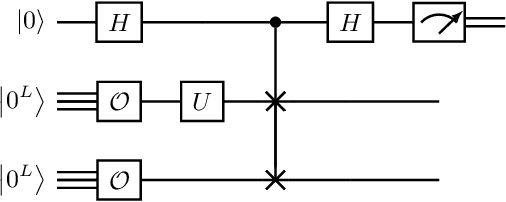
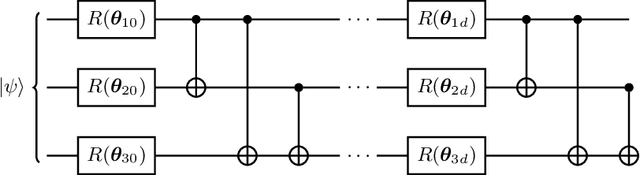
A symmetry of a state $\lvert \psi \rangle$ is a unitary operator of which $\lvert \psi \rangle$ is an eigenvector. When $\lvert \psi \rangle$ is an unknown state supplied by a black-box oracle, the state's symmetries serve to characterize it, and often relegate much of the desired information about $\lvert \psi \rangle$. In this paper, we develop a variational hybrid quantum-classical learning scheme to systematically probe for symmetries of $\lvert \psi \rangle$ with no a priori assumptions about the state. This procedure can be used to learn various symmetries at the same time. In order to avoid re-learning already known symmetries, we introduce an interactive protocol with a classical deep neural net. The classical net thereby regularizes against repetitive findings and allows our algorithm to terminate empirically with all possible symmetries found. Our scheme can be implemented efficiently on average with non-local SWAP gates; we also give a less efficient algorithm with only local operations, which may be more appropriate for current noisy quantum devices. We demonstrate our algorithm on representative families of states.