FreeInv: Free Lunch for Improving DDIM Inversion

Naive DDIM inversion process usually suffers from a trajectory deviation issue, i.e., the latent trajectory during reconstruction deviates from the one during inversion. To alleviate this issue, previous methods either learn to mitigate the deviation or design cumbersome compensation strategy to reduce the mismatch error, exhibiting substantial time and computation cost. In this work, we present a nearly free-lunch method (named FreeInv) to address the issue more effectively and efficiently. In FreeInv, we randomly transform the latent representation and keep the transformation the same between the corresponding inversion and reconstruction time-step. It is motivated from a statistical perspective that an ensemble of DDIM inversion processes for multiple trajectories yields a smaller trajectory mismatch error on expectation. Moreover, through theoretical analysis and empirical study, we show that FreeInv performs an efficient ensemble of multiple trajectories. FreeInv can be freely integrated into existing inversion-based image and video editing techniques. Especially for inverting video sequences, it brings more significant fidelity and efficiency improvements. Comprehensive quantitative and qualitative evaluation on PIE benchmark and DAVIS dataset shows that FreeInv remarkably outperforms conventional DDIM inversion, and is competitive among previous state-of-the-art inversion methods, with superior computation efficiency.

Arbitrary Polynomial Separations in Trainable Quantum Machine Learning

Recent theoretical results in quantum machine learning have demonstrated a general trade-off between the expressive power of quantum neural networks (QNNs) and their trainability; as a corollary of these results, practical exponential separations in expressive power over classical machine learning models are believed to be infeasible as such QNNs take a time to train that is exponential in the model size. We here circumvent these negative results by constructing a hierarchy of efficiently trainable QNNs that exhibit unconditionally provable, polynomial memory separations of arbitrary constant degree over classical neural networks in performing a classical sequence modeling task. Furthermore, each unit cell of the introduced class of QNNs is computationally efficient, implementable in constant time on a quantum device. The classical networks we prove a separation over include well-known examples such as recurrent neural networks and Transformers. We show that quantum contextuality is the source of the expressivity separation, suggesting that other classical sequence learning problems with long-time correlations may be a regime where practical advantages in quantum machine learning may exist.

Many-body localized hidden Born machine

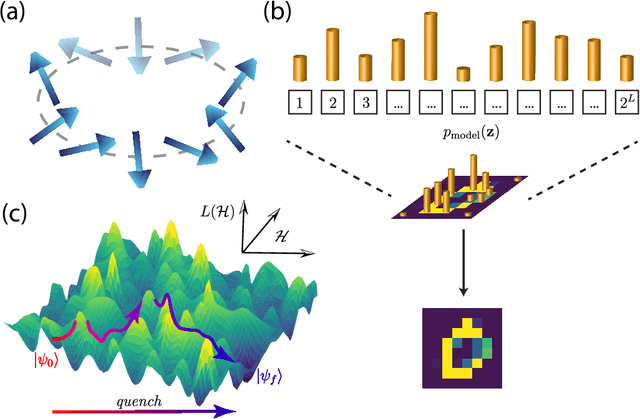
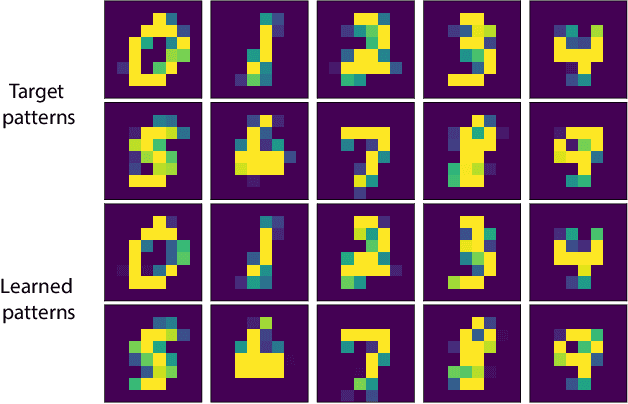
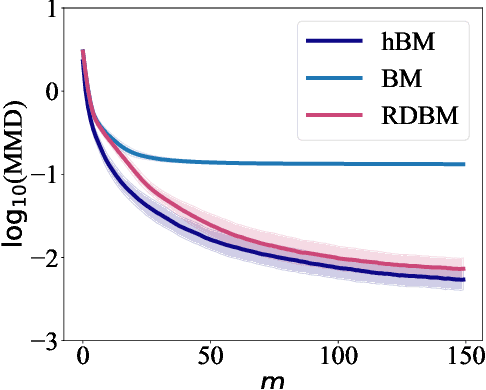
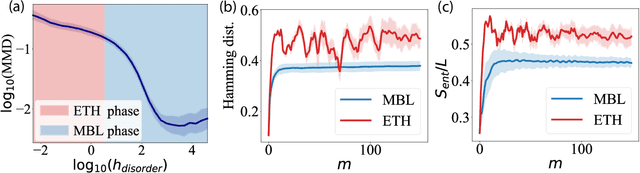
Born Machines are quantum-inspired generative models that leverage the probabilistic nature of quantum states. Here, we present a new architecture called many-body localized (MBL) hidden Born machine that uses both MBL dynamics and hidden units as learning resources. We theoretically prove that MBL Born machines possess more expressive power than classical models, and the introduction of hidden units boosts its learning power. We numerically demonstrate that the MBL hidden Born machine is capable of learning a toy dataset consisting of patterns of MNIST handwritten digits, quantum data obtained from quantum many-body states, and non-local parity data. In order to understand the mechanism behind learning, we track physical quantities such as von Neumann entanglement entropy and Hamming distance during learning, and compare the learning outcomes in the MBL, thermal, and Anderson localized phases. We show that the superior learning power of the MBL phase relies importantly on both localization and interaction. Our architecture and algorithm provide novel strategies of utilizing quantum many-body systems as learning resources, and reveal a powerful connection between disorder, interaction, and learning in quantum systems.

Pairwise Emotional Relationship Recognition in Drama Videos: Dataset and Benchmark

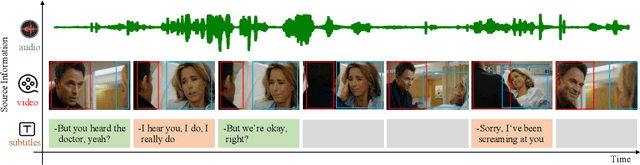
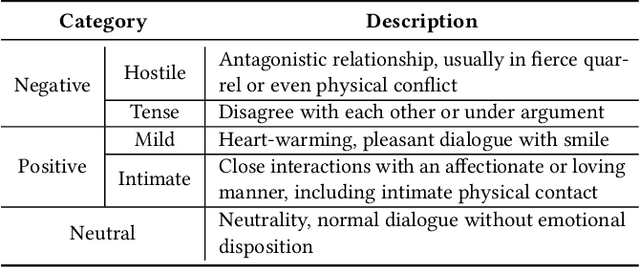
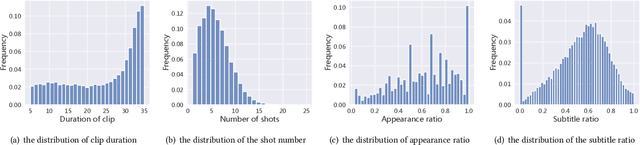
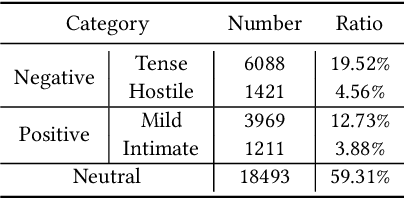
Recognizing the emotional state of people is a basic but challenging task in video understanding. In this paper, we propose a new task in this field, named Pairwise Emotional Relationship Recognition (PERR). This task aims to recognize the emotional relationship between the two interactive characters in a given video clip. It is different from the traditional emotion and social relation recognition task. Varieties of information, consisting of character appearance, behaviors, facial emotions, dialogues, background music as well as subtitles contribute differently to the final results, which makes the task more challenging but meaningful in developing more advanced multi-modal models. To facilitate the task, we develop a new dataset called Emotional RelAtionship of inTeractiOn (ERATO) based on dramas and movies. ERATO is a large-scale multi-modal dataset for PERR task, which has 31,182 video clips, lasting about 203 video hours. Different from the existing datasets, ERATO contains interaction-centric videos with multi-shots, varied video length, and multiple modalities including visual, audio and text. As a minor contribution, we propose a baseline model composed of Synchronous Modal-Temporal Attention (SMTA) unit to fuse the multi-modal information for the PERR task. In contrast to other prevailing attention mechanisms, our proposed SMTA can steadily improve the performance by about 1\%. We expect the ERATO as well as our proposed SMTA to open up a new way for PERR task in video understanding and further improve the research of multi-modal fusion methodology.

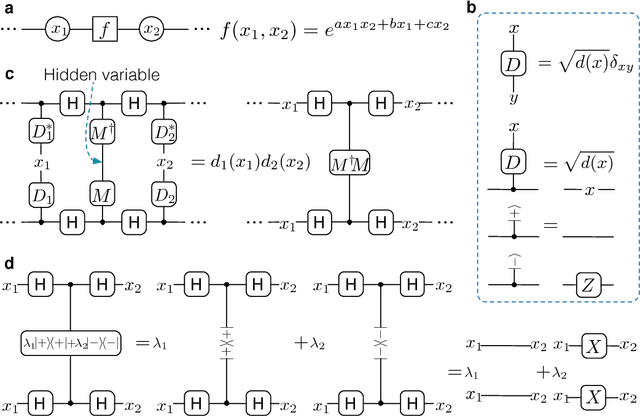
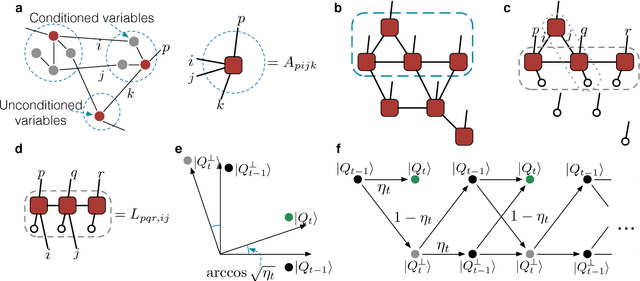
Enhancing Generative Models via Quantum Correlations

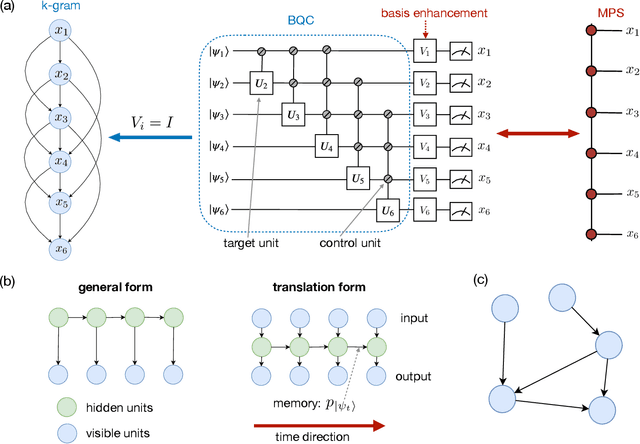
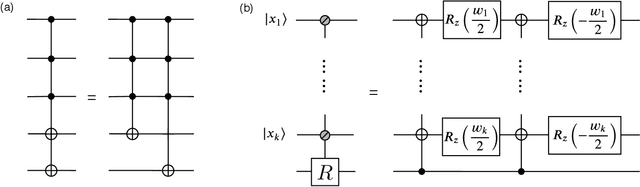
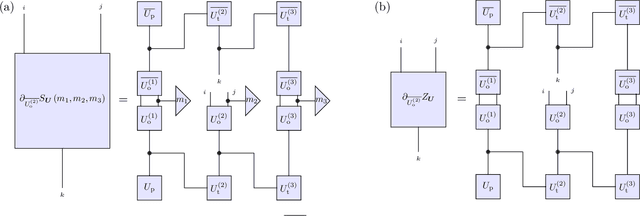
Generative modeling using samples drawn from the probability distribution constitutes a powerful approach for unsupervised machine learning. Quantum mechanical systems can produce probability distributions that exhibit quantum correlations which are difficult to capture using classical models. We show theoretically that such quantum correlations provide a powerful resource for generative modeling. In particular, we provide an unconditional proof of separation in expressive power between a class of widely-used generative models, known as Bayesian networks, and its minimal quantum extension. We show that this expressivity advantage is associated with quantum nonlocality and quantum contextuality. Furthermore, we numerically test this separation on standard machine learning data sets and show that it holds for practical problems. The possibility of quantum advantage demonstrated in this work not only sheds light on the design of useful quantum machine learning protocols but also provides inspiration to draw on ideas from quantum foundations to improve purely classical algorithms.

An efficient quantum algorithm for generative machine learning

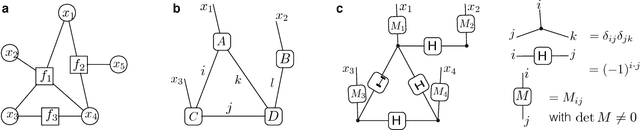
A central task in the field of quantum computing is to find applications where quantum computer could provide exponential speedup over any classical computer. Machine learning represents an important field with broad applications where quantum computer may offer significant speedup. Several quantum algorithms for discriminative machine learning have been found based on efficient solving of linear algebraic problems, with potential exponential speedup in runtime under the assumption of effective input from a quantum random access memory. In machine learning, generative models represent another large class which is widely used for both supervised and unsupervised learning. Here, we propose an efficient quantum algorithm for machine learning based on a quantum generative model. We prove that our proposed model is exponentially more powerful to represent probability distributions compared with classical generative models and has exponential speedup in training and inference at least for some instances under a reasonable assumption in computational complexity theory. Our result opens a new direction for quantum machine learning and offers a remarkable example in which a quantum algorithm shows exponential improvement over any classical algorithm in an important application field.