Learning topological states from randomized measurements using variational tensor network tomography

Learning faithful representations of quantum states is crucial to fully characterizing the variety of many-body states created on quantum processors. While various tomographic methods such as classical shadow and MPS tomography have shown promise in characterizing a wide class of quantum states, they face unique limitations in detecting topologically ordered two-dimensional states. To address this problem, we implement and study a heuristic tomographic method that combines variational optimization on tensor networks with randomized measurement techniques. Using this approach, we demonstrate its ability to learn the ground state of the surface code Hamiltonian as well as an experimentally realizable quantum spin liquid state. In particular, we perform numerical experiments using MPS ans\"atze and systematically investigate the sample complexity required to achieve high fidelities for systems of sizes up to $48$ qubits. In addition, we provide theoretical insights into the scaling of our learning algorithm by analyzing the statistical properties of maximum likelihood estimation. Notably, our method is sample-efficient and experimentally friendly, only requiring snapshots of the quantum state measured randomly in the $X$ or $Z$ bases. Using this subset of measurements, our approach can effectively learn any real pure states represented by tensor networks, and we rigorously prove that random-$XZ$ measurements are tomographically complete for such states.

Many-body localized hidden Born machine

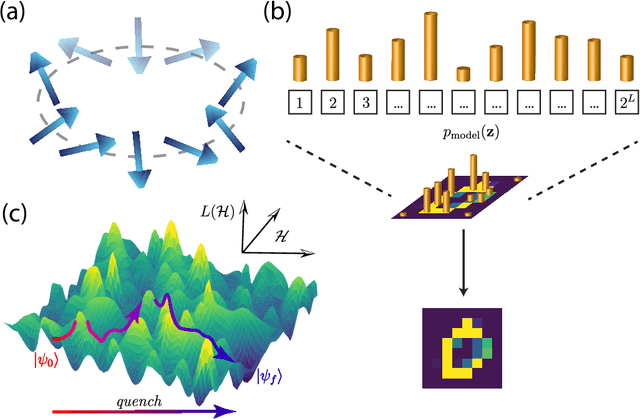
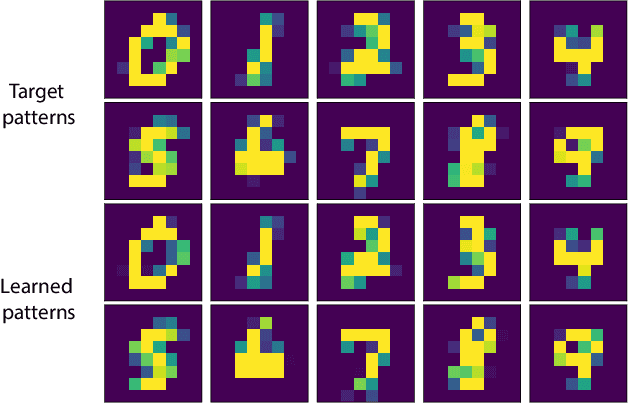
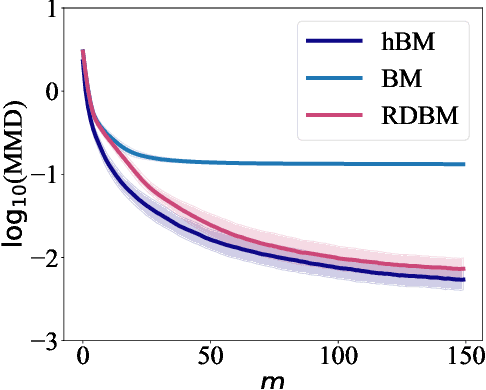
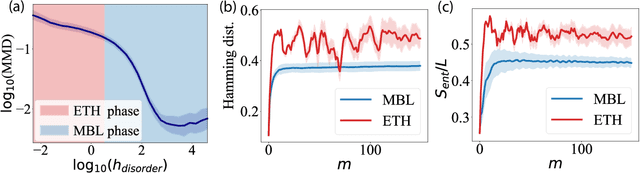
Born Machines are quantum-inspired generative models that leverage the probabilistic nature of quantum states. Here, we present a new architecture called many-body localized (MBL) hidden Born machine that uses both MBL dynamics and hidden units as learning resources. We theoretically prove that MBL Born machines possess more expressive power than classical models, and the introduction of hidden units boosts its learning power. We numerically demonstrate that the MBL hidden Born machine is capable of learning a toy dataset consisting of patterns of MNIST handwritten digits, quantum data obtained from quantum many-body states, and non-local parity data. In order to understand the mechanism behind learning, we track physical quantities such as von Neumann entanglement entropy and Hamming distance during learning, and compare the learning outcomes in the MBL, thermal, and Anderson localized phases. We show that the superior learning power of the MBL phase relies importantly on both localization and interaction. Our architecture and algorithm provide novel strategies of utilizing quantum many-body systems as learning resources, and reveal a powerful connection between disorder, interaction, and learning in quantum systems.

Learning quantum symmetries with interactive quantum-classical variational algorithms

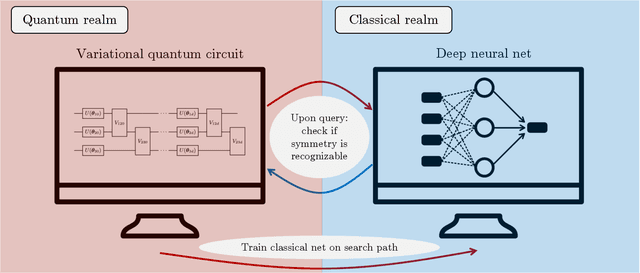
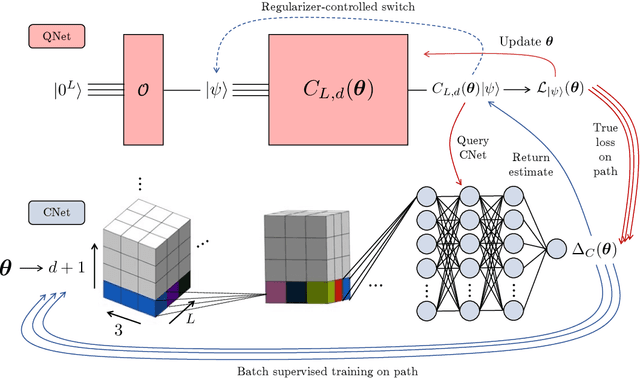
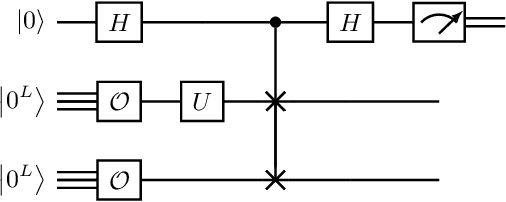
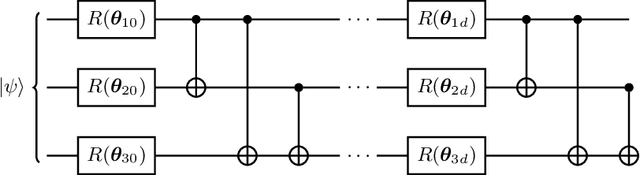
A symmetry of a state $\lvert \psi \rangle$ is a unitary operator of which $\lvert \psi \rangle$ is an eigenvector. When $\lvert \psi \rangle$ is an unknown state supplied by a black-box oracle, the state's symmetries serve to characterize it, and often relegate much of the desired information about $\lvert \psi \rangle$. In this paper, we develop a variational hybrid quantum-classical learning scheme to systematically probe for symmetries of $\lvert \psi \rangle$ with no a priori assumptions about the state. This procedure can be used to learn various symmetries at the same time. In order to avoid re-learning already known symmetries, we introduce an interactive protocol with a classical deep neural net. The classical net thereby regularizes against repetitive findings and allows our algorithm to terminate empirically with all possible symmetries found. Our scheme can be implemented efficiently on average with non-local SWAP gates; we also give a less efficient algorithm with only local operations, which may be more appropriate for current noisy quantum devices. We demonstrate our algorithm on representative families of states.

An analytic theory for the dynamics of wide quantum neural networks

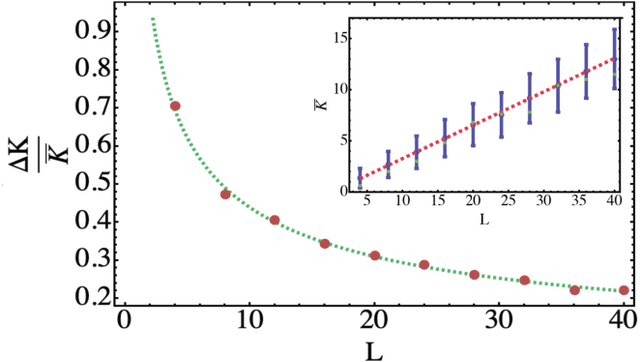
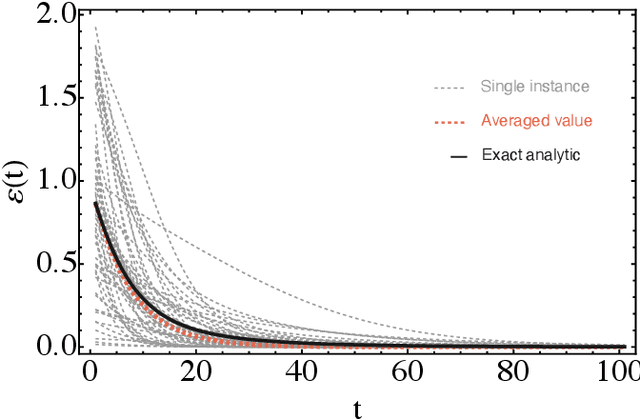
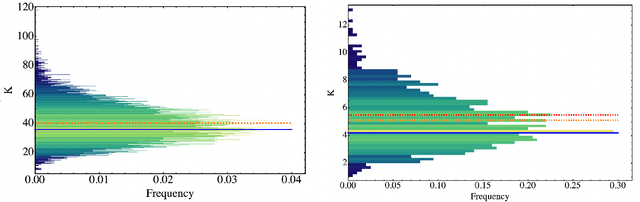
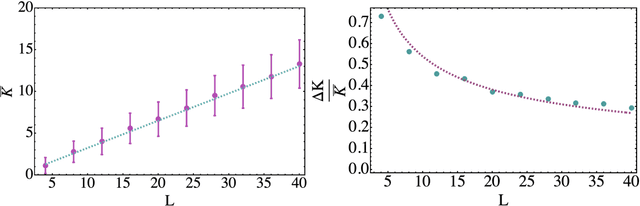
Parametrized quantum circuits can be used as quantum neural networks and have the potential to outperform their classical counterparts when trained for addressing learning problems. To date, much of the results on their performance on practical problems are heuristic in nature. In particular, the convergence rate for the training of quantum neural networks is not fully understood. Here, we analyze the dynamics of gradient descent for the training error of a class of variational quantum machine learning models. We define wide quantum neural networks as parameterized quantum circuits in the limit of a large number of qubits and variational parameters. We then find a simple analytic formula that captures the average behavior of their loss function and discuss the consequences of our findings. For example, for random quantum circuits, we predict and characterize an exponential decay of the residual training error as a function of the parameters of the system. We finally validate our analytic results with numerical experiments.