Towards efficient quantum algorithms for diffusion probability models

A diffusion probabilistic model (DPM) is a generative model renowned for its ability to produce high-quality outputs in tasks such as image and audio generation. However, training DPMs on large, high-dimensional datasets such as high-resolution images or audio incurs significant computational, energy, and hardware costs. In this work, we introduce efficient quantum algorithms for implementing DPMs through various quantum ODE solvers. These algorithms highlight the potential of quantum Carleman linearization for diverse mathematical structures, leveraging state-of-the-art quantum linear system solvers (QLSS) or linear combination of Hamiltonian simulations (LCHS). Specifically, we focus on two approaches: DPM-solver-$k$ which employs exact $k$-th order derivatives to compute a polynomial approximation of $\epsilon_\theta(x_\lambda,\lambda)$; and UniPC which uses finite difference of $\epsilon_\theta(x_\lambda,\lambda)$ at different points $(x_{s_m}, \lambda_{s_m})$ to approximate higher-order derivatives. As such, this work represents one of the most direct and pragmatic applications of quantum algorithms to large-scale machine learning models, presumably talking substantial steps towards demonstrating the practical utility of quantum computing.

Opportunities and limitations of explaining quantum machine learning

A common trait of many machine learning models is that it is often difficult to understand and explain what caused the model to produce the given output. While the explainability of neural networks has been an active field of research in the last years, comparably little is known for quantum machine learning models. Despite a few recent works analyzing some specific aspects of explainability, as of now there is no clear big picture perspective as to what can be expected from quantum learning models in terms of explainability. In this work, we address this issue by identifying promising research avenues in this direction and lining out the expected future results. We additionally propose two explanation methods designed specifically for quantum machine learning models, as first of their kind to the best of our knowledge. Next to our pre-view of the field, we compare both existing and novel methods to explain the predictions of quantum learning models. By studying explainability in quantum machine learning, we can contribute to the sustainable development of the field, preventing trust issues in the future.

Interactive proofs for verifying (quantum) learning and testing

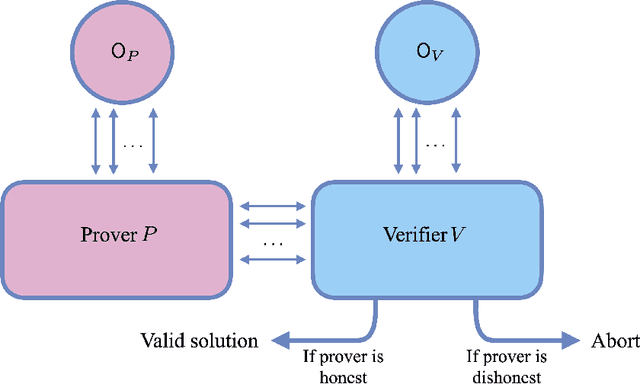
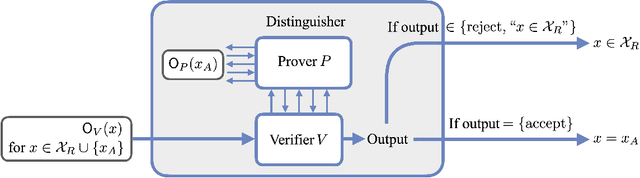
We consider the problem of testing and learning from data in the presence of resource constraints, such as limited memory or weak data access, which place limitations on the efficiency and feasibility of testing or learning. In particular, we ask the following question: Could a resource-constrained learner/tester use interaction with a resource-unconstrained but untrusted party to solve a learning or testing problem more efficiently than they could without such an interaction? In this work, we answer this question both abstractly and for concrete problems, in two complementary ways: For a wide variety of scenarios, we prove that a resource-constrained learner cannot gain any advantage through classical interaction with an untrusted prover. As a special case, we show that for the vast majority of testing and learning problems in which quantum memory is a meaningful resource, a memory-constrained quantum algorithm cannot overcome its limitations via classical communication with a memory-unconstrained quantum prover. In contrast, when quantum communication is allowed, we construct a variety of interactive proof protocols, for specific learning and testing problems, which allow memory-constrained quantum verifiers to gain significant advantages through delegation to untrusted provers. These results highlight both the limitations and potential of delegating learning and testing problems to resource-rich but untrusted third parties.

Artificially intelligent Maxwell's demon for optimal control of open quantum systems

Feedback control of open quantum systems is of fundamental importance for practical applications in various contexts, ranging from quantum computation to quantum error correction and quantum metrology. Its use in the context of thermodynamics further enables the study of the interplay between information and energy. However, deriving optimal feedback control strategies is highly challenging, as it involves the optimal control of open quantum systems, the stochastic nature of quantum measurement, and the inclusion of policies that maximize a long-term time- and trajectory-averaged goal. In this work, we employ a reinforcement learning approach to automate and capture the role of a quantum Maxwell's demon: the agent takes the literal role of discovering optimal feedback control strategies in qubit-based systems that maximize a trade-off between measurement-powered cooling and measurement efficiency. Considering weak or projective quantum measurements, we explore different regimes based on the ordering between the thermalization, the measurement, and the unitary feedback timescales, finding different and highly non-intuitive, yet interpretable, strategies. In the thermalization-dominated regime, we find strategies with elaborate finite-time thermalization protocols conditioned on measurement outcomes. In the measurement-dominated regime, we find that optimal strategies involve adaptively measuring different qubit observables reflecting the acquired information, and repeating multiple weak measurements until the quantum state is "sufficiently pure", leading to random walks in state space. Finally, we study the case when all timescales are comparable, finding new feedback control strategies that considerably outperform more intuitive ones. We discuss a two-qubit example where we explore the role of entanglement and conclude discussing the scaling of our results to quantum many-body systems.

Online learning of quantum processes

Among recent insights into learning quantum states, online learning and shadow tomography procedures are notable for their ability to accurately predict expectation values even of adaptively chosen observables. In contrast to the state case, quantum process learning tasks with a similarly adaptive nature have received little attention. In this work, we investigate online learning tasks for quantum processes. Whereas online learning is infeasible for general quantum channels, we show that channels of bounded gate complexity as well as Pauli channels can be online learned in the regret and mistake-bounded models of online learning. In fact, we can online learn probabilistic mixtures of any exponentially large set of known channels. We also provide a provably sample-efficient shadow tomography procedure for Pauli channels. Our results extend beyond quantum channels to non-Markovian multi-time processes, with favorable regret and mistake bounds, as well as a shadow tomography procedure. We complement our online learning upper bounds with mistake as well as computational lower bounds. On the technical side, we make use of the multiplicative weights update algorithm, classical adaptive data analysis, and Bell sampling, as well as tools from the theory of quantum combs for multi-time quantum processes. Our work initiates a study of online learning for classes of quantum channels and, more generally, non-Markovian quantum processes. Given the importance of online learning for state shadow tomography, this may serve as a step towards quantum channel variants of adaptive shadow tomography.

Learning topological states from randomized measurements using variational tensor network tomography

Learning faithful representations of quantum states is crucial to fully characterizing the variety of many-body states created on quantum processors. While various tomographic methods such as classical shadow and MPS tomography have shown promise in characterizing a wide class of quantum states, they face unique limitations in detecting topologically ordered two-dimensional states. To address this problem, we implement and study a heuristic tomographic method that combines variational optimization on tensor networks with randomized measurement techniques. Using this approach, we demonstrate its ability to learn the ground state of the surface code Hamiltonian as well as an experimentally realizable quantum spin liquid state. In particular, we perform numerical experiments using MPS ans\"atze and systematically investigate the sample complexity required to achieve high fidelities for systems of sizes up to $48$ qubits. In addition, we provide theoretical insights into the scaling of our learning algorithm by analyzing the statistical properties of maximum likelihood estimation. Notably, our method is sample-efficient and experimentally friendly, only requiring snapshots of the quantum state measured randomly in the $X$ or $Z$ bases. Using this subset of measurements, our approach can effectively learn any real pure states represented by tensor networks, and we rigorously prove that random-$XZ$ measurements are tomographically complete for such states.

On the expressivity of embedding quantum kernels

One of the most natural connections between quantum and classical machine learning has been established in the context of kernel methods. Kernel methods rely on kernels, which are inner products of feature vectors living in large feature spaces. Quantum kernels are typically evaluated by explicitly constructing quantum feature states and then taking their inner product, here called embedding quantum kernels. Since classical kernels are usually evaluated without using the feature vectors explicitly, we wonder how expressive embedding quantum kernels are. In this work, we raise the fundamental question: can all quantum kernels be expressed as the inner product of quantum feature states? Our first result is positive: Invoking computational universality, we find that for any kernel function there always exists a corresponding quantum feature map and an embedding quantum kernel. The more operational reading of the question is concerned with efficient constructions, however. In a second part, we formalize the question of universality of efficient embedding quantum kernels. For shift-invariant kernels, we use the technique of random Fourier features to show that they are universal within the broad class of all kernels which allow a variant of efficient Fourier sampling. We then extend this result to a new class of so-called composition kernels, which we show also contains projected quantum kernels introduced in recent works. After proving the universality of embedding quantum kernels for both shift-invariant and composition kernels, we identify the directions towards new, more exotic, and unexplored quantum kernel families, for which it still remains open whether they correspond to efficient embedding quantum kernels.

Potential and limitations of random Fourier features for dequantizing quantum machine learning

Quantum machine learning is arguably one of the most explored applications of near-term quantum devices. Much focus has been put on notions of variational quantum machine learning where parameterized quantum circuits (PQCs) are used as learning models. These PQC models have a rich structure which suggests that they might be amenable to efficient dequantization via random Fourier features (RFF). In this work, we establish necessary and sufficient conditions under which RFF does indeed provide an efficient dequantization of variational quantum machine learning for regression. We build on these insights to make concrete suggestions for PQC architecture design, and to identify structures which are necessary for a regression problem to admit a potential quantum advantage via PQC based optimization.

Understanding quantum machine learning also requires rethinking generalization

Quantum machine learning models have shown successful generalization performance even when trained with few data. In this work, through systematic randomization experiments, we show that traditional approaches to understanding generalization fail to explain the behavior of such quantum models. Our experiments reveal that state-of-the-art quantum neural networks accurately fit random states and random labeling of training data. This ability to memorize random data defies current notions of small generalization error, problematizing approaches that build on complexity measures such as the VC dimension, the Rademacher complexity, and all their uniform relatives. We complement our empirical results with a theoretical construction showing that quantum neural networks can fit arbitrary labels to quantum states, hinting at their memorization ability. Our results do not preclude the possibility of good generalization with few training data but rather rule out any possible guarantees based only on the properties of the model family. These findings expose a fundamental challenge in the conventional understanding of generalization in quantum machine learning and highlight the need for a paradigm shift in the design of quantum models for machine learning tasks.

On the average-case complexity of learning output distributions of quantum circuits

In this work, we show that learning the output distributions of brickwork random quantum circuits is average-case hard in the statistical query model. This learning model is widely used as an abstract computational model for most generic learning algorithms. In particular, for brickwork random quantum circuits on $n$ qubits of depth $d$, we show three main results: - At super logarithmic circuit depth $d=\omega(\log(n))$, any learning algorithm requires super polynomially many queries to achieve a constant probability of success over the randomly drawn instance. - There exists a $d=O(n)$, such that any learning algorithm requires $\Omega(2^n)$ queries to achieve a $O(2^{-n})$ probability of success over the randomly drawn instance. - At infinite circuit depth $d\to\infty$, any learning algorithm requires $2^{2^{\Omega(n)}}$ many queries to achieve a $2^{-2^{\Omega(n)}}$ probability of success over the randomly drawn instance. As an auxiliary result of independent interest, we show that the output distribution of a brickwork random quantum circuit is constantly far from any fixed distribution in total variation distance with probability $1-O(2^{-n})$, which confirms a variant of a conjecture by Aaronson and Chen.