A quantum-classical reinforcement learning model to play Atari games

Recent advances in reinforcement learning have demonstrated the potential of quantum learning models based on parametrized quantum circuits as an alternative to deep learning models. On the one hand, these findings have shown the ultimate exponential speed-ups in learning that full-blown quantum models can offer in certain -- artificially constructed -- environments. On the other hand, they have demonstrated the ability of experimentally accessible PQCs to solve OpenAI Gym benchmarking tasks. However, it remains an open question whether these near-term QRL techniques can be successfully applied to more complex problems exhibiting high-dimensional observation spaces. In this work, we bridge this gap and present a hybrid model combining a PQC with classical feature encoding and post-processing layers that is capable of tackling Atari games. A classical model, subjected to architectural restrictions similar to those present in the hybrid model is constructed to serve as a reference. Our numerical investigation demonstrates that the proposed hybrid model is capable of solving the Pong environment and achieving scores comparable to the classical reference in Breakout. Furthermore, our findings shed light on important hyperparameter settings and design choices that impact the interplay of the quantum and classical components. This work contributes to the understanding of near-term quantum learning models and makes an important step towards their deployment in real-world RL scenarios.

Variational measurement-based quantum computation for generative modeling

Measurement-based quantum computation (MBQC) offers a fundamentally unique paradigm to design quantum algorithms. Indeed, due to the inherent randomness of quantum measurements, the natural operations in MBQC are not deterministic and unitary, but are rather augmented with probabilistic byproducts. Yet, the main algorithmic use of MBQC so far has been to completely counteract this probabilistic nature in order to simulate unitary computations expressed in the circuit model. In this work, we propose designing MBQC algorithms that embrace this inherent randomness and treat the random byproducts in MBQC as a resource for computation. As a natural application where randomness can be beneficial, we consider generative modeling, a task in machine learning centered around generating complex probability distributions. To address this task, we propose a variational MBQC algorithm equipped with control parameters that allow to directly adjust the degree of randomness to be admitted in the computation. Our numerical findings indicate that this additional randomness can lead to significant gains in learning performance in certain generative modeling tasks. These results highlight the potential advantages in exploiting the inherent randomness of MBQC and motivate further research into MBQC-based algorithms.

Potential and limitations of random Fourier features for dequantizing quantum machine learning

Quantum machine learning is arguably one of the most explored applications of near-term quantum devices. Much focus has been put on notions of variational quantum machine learning where parameterized quantum circuits (PQCs) are used as learning models. These PQC models have a rich structure which suggests that they might be amenable to efficient dequantization via random Fourier features (RFF). In this work, we establish necessary and sufficient conditions under which RFF does indeed provide an efficient dequantization of variational quantum machine learning for regression. We build on these insights to make concrete suggestions for PQC architecture design, and to identify structures which are necessary for a regression problem to admit a potential quantum advantage via PQC based optimization.

Shadows of quantum machine learning

Quantum machine learning is often highlighted as one of the most promising uses for a quantum computer to solve practical problems. However, a major obstacle to the widespread use of quantum machine learning models in practice is that these models, even once trained, still require access to a quantum computer in order to be evaluated on new data. To solve this issue, we suggest that following the training phase of a quantum model, a quantum computer could be used to generate what we call a classical shadow of this model, i.e., a classically computable approximation of the learned function. While recent works already explore this idea and suggest approaches to construct such shadow models, they also raise the possibility that a completely classical model could be trained instead, thus circumventing the need for a quantum computer in the first place. In this work, we take a novel approach to define shadow models based on the frameworks of quantum linear models and classical shadow tomography. This approach allows us to show that there exist shadow models which can solve certain learning tasks that are intractable for fully classical models, based on widely-believed cryptography assumptions. We also discuss the (un)likeliness that all quantum models could be shadowfiable, based on common assumptions in complexity theory.

The power and limitations of learning quantum dynamics incoherently

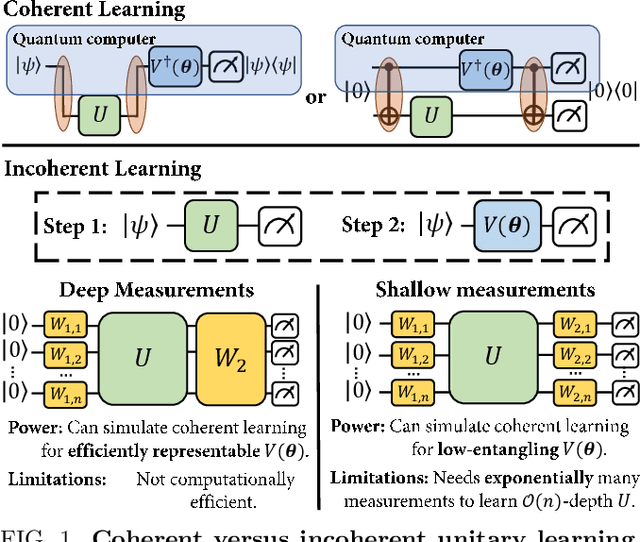
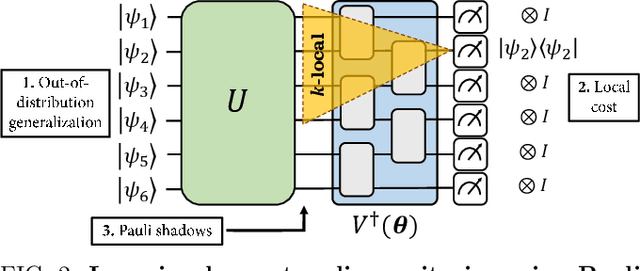
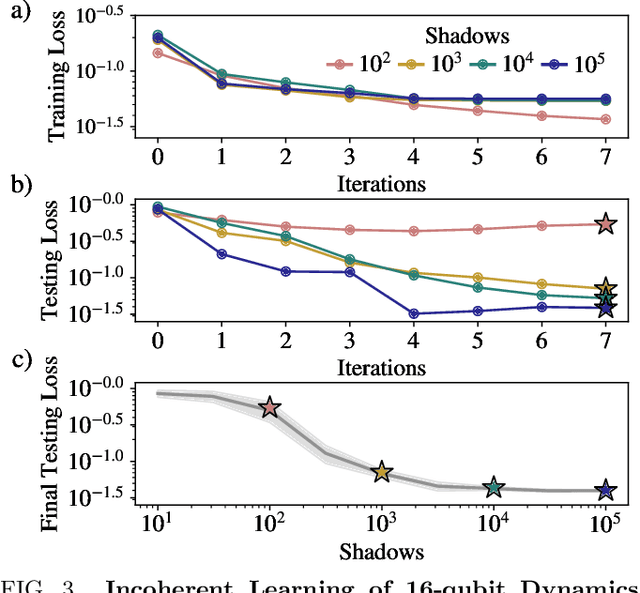
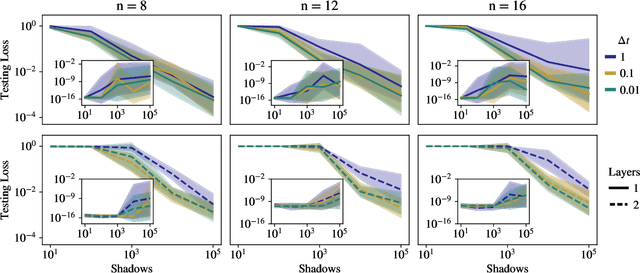
Quantum process learning is emerging as an important tool to study quantum systems. While studied extensively in coherent frameworks, where the target and model system can share quantum information, less attention has been paid to whether the dynamics of quantum systems can be learned without the system and target directly interacting. Such incoherent frameworks are practically appealing since they open up methods of transpiling quantum processes between the different physical platforms without the need for technically challenging hybrid entanglement schemes. Here we provide bounds on the sample complexity of learning unitary processes incoherently by analyzing the number of measurements that are required to emulate well-established coherent learning strategies. We prove that if arbitrary measurements are allowed, then any efficiently representable unitary can be efficiently learned within the incoherent framework; however, when restricted to shallow-depth measurements only low-entangling unitaries can be learned. We demonstrate our incoherent learning algorithm for low entangling unitaries by successfully learning a 16-qubit unitary on \texttt{ibmq\_kolkata}, and further demonstrate the scalabilty of our proposed algorithm through extensive numerical experiments.

Quantum policy gradient algorithms

Understanding the power and limitations of quantum access to data in machine learning tasks is primordial to assess the potential of quantum computing in artificial intelligence. Previous works have already shown that speed-ups in learning are possible when given quantum access to reinforcement learning environments. Yet, the applicability of quantum algorithms in this setting remains very limited, notably in environments with large state and action spaces. In this work, we design quantum algorithms to train state-of-the-art reinforcement learning policies by exploiting quantum interactions with an environment. However, these algorithms only offer full quadratic speed-ups in sample complexity over their classical analogs when the trained policies satisfy some regularity conditions. Interestingly, we find that reinforcement learning policies derived from parametrized quantum circuits are well-behaved with respect to these conditions, which showcases the benefit of a fully-quantum reinforcement learning framework.

Reinforcement Learning Assisted Recursive QAOA

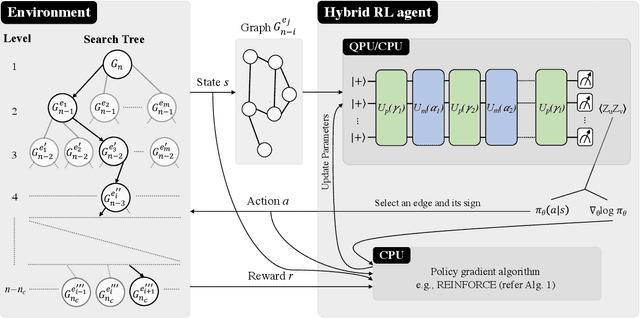
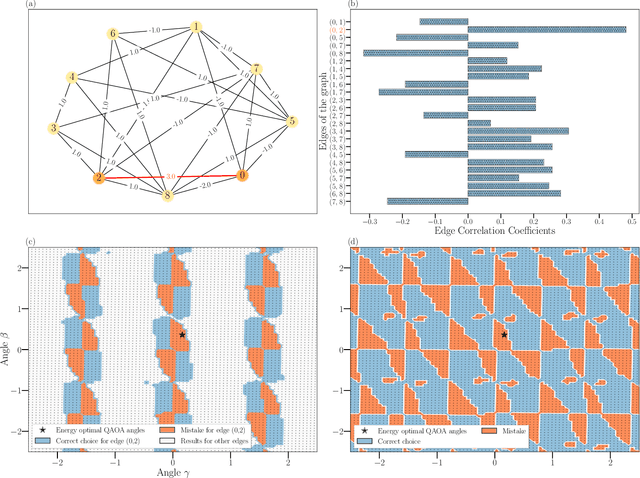
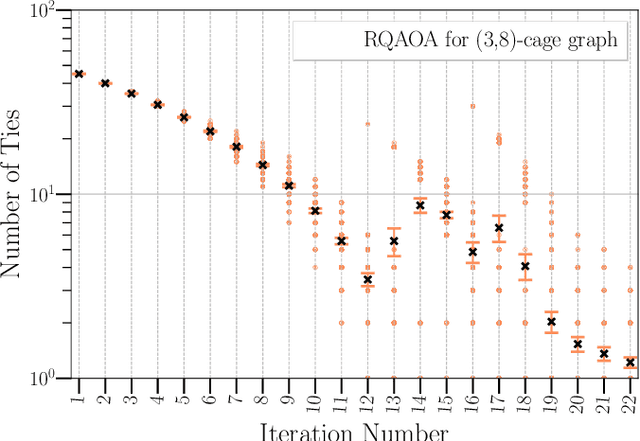
Variational quantum algorithms such as the Quantum Approximation Optimization Algorithm (QAOA) in recent years have gained popularity as they provide the hope of using NISQ devices to tackle hard combinatorial optimization problems. It is, however, known that at low depth, certain locality constraints of QAOA limit its performance. To go beyond these limitations, a non-local variant of QAOA, namely recursive QAOA (RQAOA), was proposed to improve the quality of approximate solutions. The RQAOA has been studied comparatively less than QAOA, and it is less understood, for instance, for what family of instances it may fail to provide high quality solutions. However, as we are tackling $\mathsf{NP}$-hard problems (specifically, the Ising spin model), it is expected that RQAOA does fail, raising the question of designing even better quantum algorithms for combinatorial optimization. In this spirit, we identify and analyze cases where RQAOA fails and, based on this, propose a reinforcement learning enhanced RQAOA variant (RL-RQAOA) that improves upon RQAOA. We show that the performance of RL-RQAOA improves over RQAOA: RL-RQAOA is strictly better on these identified instances where RQAOA underperforms, and is similarly performing on instances where RQAOA is near-optimal. Our work exemplifies the potentially beneficial synergy between reinforcement learning and quantum (inspired) optimization in the design of new, even better heuristics for hard problems.

Near-Optimal Quantum Algorithms for Multivariate Mean Estimation

We propose the first near-optimal quantum algorithm for estimating in Euclidean norm the mean of a vector-valued random variable with finite mean and covariance. Our result aims at extending the theory of multivariate sub-Gaussian estimators to the quantum setting. Unlike classically, where any univariate estimator can be turned into a multivariate estimator with at most a logarithmic overhead in the dimension, no similar result can be proved in the quantum setting. Indeed, Heinrich ruled out the existence of a quantum advantage for the mean estimation problem when the sample complexity is smaller than the dimension. Our main result is to show that, outside this low-precision regime, there is a quantum estimator that outperforms any classical estimator. Our approach is substantially more involved than in the univariate setting, where most quantum estimators rely only on phase estimation. We exploit a variety of additional algorithmic techniques such as amplitude amplification, the Bernstein-Vazirani algorithm, and quantum singular value transformation. Our analysis also uses concentration inequalities for multivariate truncated statistics. We develop our quantum estimators in two different input models that showed up in the literature before. The first one provides coherent access to the binary representation of the random variable and it encompasses the classical setting. In the second model, the random variable is directly encoded into the phases of quantum registers. This model arises naturally in many quantum algorithms but it is often incomparable to having classical samples. We adapt our techniques to these two settings and we show that the second model is strictly weaker for solving the mean estimation problem. Finally, we describe several applications of our algorithms, notably in measuring the expectation values of commuting observables and in the field of machine learning.

Quantum machine learning beyond kernel methods

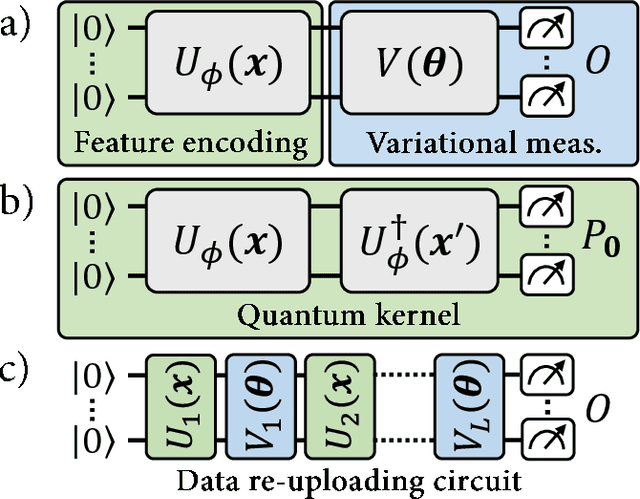
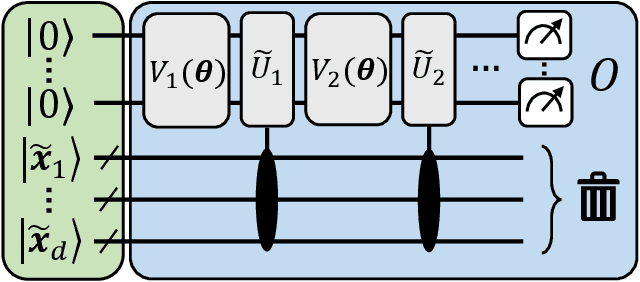
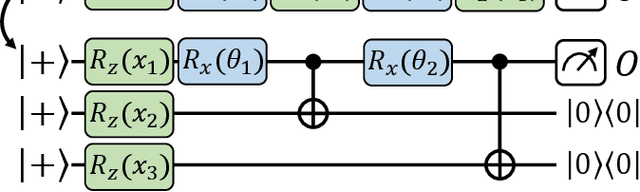
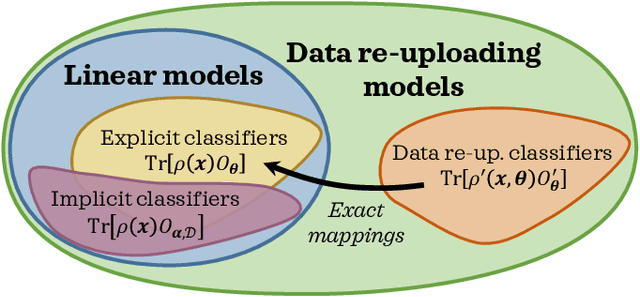
With noisy intermediate-scale quantum computers showing great promise for near-term applications, a number of machine learning algorithms based on parametrized quantum circuits have been suggested as possible means to achieve learning advantages. Yet, our understanding of how these quantum machine learning models compare, both to existing classical models and to each other, remains limited. A big step in this direction has been made by relating them to so-called kernel methods from classical machine learning. By building on this connection, previous works have shown that a systematic reformulation of many quantum machine learning models as kernel models was guaranteed to improve their training performance. In this work, we first extend the applicability of this result to a more general family of parametrized quantum circuit models called data re-uploading circuits. Secondly, we show, through simple constructions and numerical simulations, that models defined and trained variationally can exhibit a critically better generalization performance than their kernel formulations, which is the true figure of merit of machine learning tasks. Our results constitute another step towards a more comprehensive theory of quantum machine learning models next to kernel formulations.

Variational quantum policies for reinforcement learning

Variational quantum circuits have recently gained popularity as quantum machine learning models. While considerable effort has been invested to train them in supervised and unsupervised learning settings, relatively little attention has been given to their potential use in reinforcement learning. In this work, we leverage the understanding of quantum policy gradient algorithms in a number of ways. First, we investigate how to construct and train reinforcement learning policies based on variational quantum circuits. We propose several designs for quantum policies, provide their learning algorithms, and test their performance on classical benchmarking environments. Second, we show the existence of task environments with a provable separation in performance between quantum learning agents and any polynomial-time classical learner, conditioned on the widely-believed classical hardness of the discrete logarithm problem. We also consider more natural settings, in which we show an empirical quantum advantage of our quantum policies over standard neural-network policies. Our results constitute a first step towards establishing a practical near-term quantum advantage in a reinforcement learning setting. Additionally, we believe that some of our design choices for variational quantum policies may also be beneficial to other models based on variational quantum circuits, such as quantum classifiers and quantum regression models.