The Work Capacity of Channels with Memory: Maximum Extractable Work in Percept-Action Loops

Predicting future observations plays a central role in machine learning, biology, economics, and many other fields. It lies at the heart of organizational principles such as the variational free energy principle and has even been shown -- based on the second law of thermodynamics -- to be necessary for reaching the fundamental energetic limits of sequential information processing. While the usefulness of the predictive paradigm is undisputed, complex adaptive systems that interact with their environment are more than just predictive machines: they have the power to act upon their environment and cause change. In this work, we develop a framework to analyze the thermodynamics of information processing in percept-action loops -- a model of agent-environment interaction -- allowing us to investigate the thermodynamic implications of actions and percepts on equal footing. To this end, we introduce the concept of work capacity -- the maximum rate at which an agent can expect to extract work from its environment. Our results reveal that neither of two previously established design principles for work-efficient agents -- maximizing predictive power and forgetting past actions -- remains optimal in environments where actions have observable consequences. Instead, a trade-off emerges: work-efficient agents must balance prediction and forgetting, as remembering past actions can reduce the available free energy. This highlights a fundamental departure from the thermodynamics of passive observation, suggesting that prediction and energy efficiency may be at odds in active learning systems.

Free Energy Projective Simulation (FEPS): Active inference with interpretability

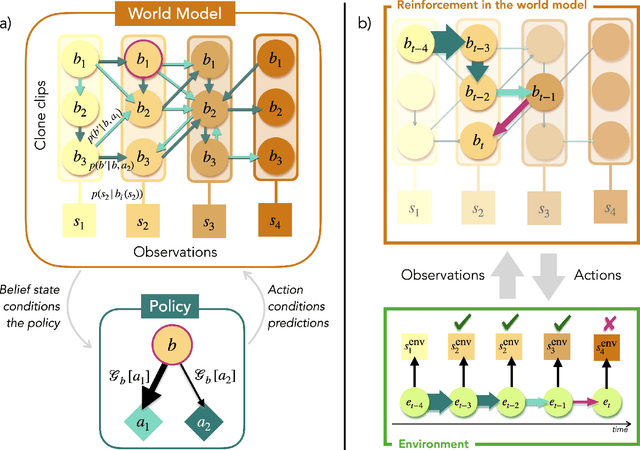
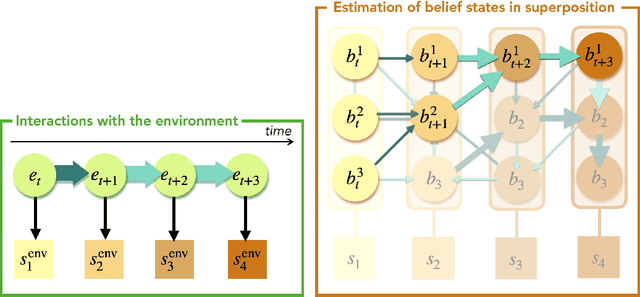
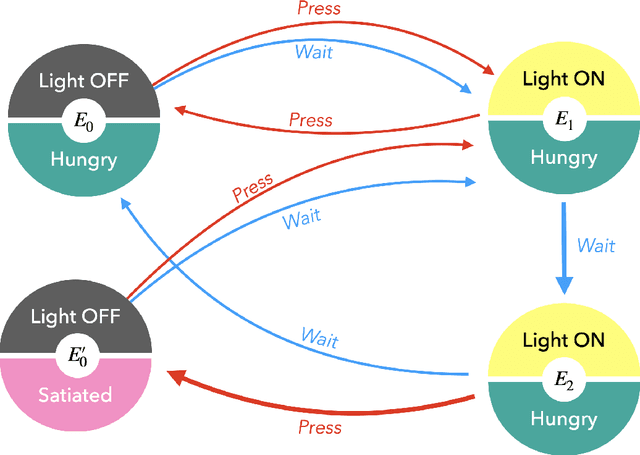
In the last decade, the free energy principle (FEP) and active inference (AIF) have achieved many successes connecting conceptual models of learning and cognition to mathematical models of perception and action. This effort is driven by a multidisciplinary interest in understanding aspects of self-organizing complex adaptive systems, including elements of agency. Various reinforcement learning (RL) models performing active inference have been proposed and trained on standard RL tasks using deep neural networks. Recent work has focused on improving such agents' performance in complex environments by incorporating the latest machine learning techniques. In this paper, we take an alternative approach. Within the constraints imposed by the FEP and AIF, we attempt to model agents in an interpretable way without deep neural networks by introducing Free Energy Projective Simulation (FEPS). Using internal rewards only, FEPS agents build a representation of their partially observable environments with which they interact. Following AIF, the policy to achieve a given task is derived from this world model by minimizing the expected free energy. Leveraging the interpretability of the model, techniques are introduced to deal with long-term goals and reduce prediction errors caused by erroneous hidden state estimation. We test the FEPS model on two RL environments inspired from behavioral biology: a timed response task and a navigation task in a partially observable grid. Our results show that FEPS agents fully resolve the ambiguity of both environments by appropriately contextualizing their observations based on prediction accuracy only. In addition, they infer optimal policies flexibly for any target observation in the environment.

Optimal foraging strategies can be learned and outperform Lévy walks

L\'evy walks and other theoretical models of optimal foraging have been successfully used to describe real-world scenarios, attracting attention in several fields such as economy, physics, ecology, and evolutionary biology. However, it remains unclear in most cases which strategies maximize foraging efficiency and whether such strategies can be learned by living organisms. To address these questions, we model foragers as reinforcement learning agents. We first prove theoretically that maximizing rewards in our reinforcement learning model is equivalent to optimizing foraging efficiency. We then show with numerical experiments that our agents learn foraging strategies which outperform the efficiency of known strategies such as L\'evy walks.

Reinforcement learning and decision making via single-photon quantum walks

Variational quantum algorithms represent a promising approach to quantum machine learning where classical neural networks are replaced by parametrized quantum circuits. Here, we present a variational approach to quantize projective simulation (PS), a reinforcement learning model aimed at interpretable artificial intelligence. Decision making in PS is modeled as a random walk on a graph describing the agent's memory. To implement the quantized model, we consider quantum walks of single photons in a lattice of tunable Mach-Zehnder interferometers. We propose variational algorithms tailored to reinforcement learning tasks, and we show, using an example from transfer learning, that the quantized PS learning model can outperform its classical counterpart. Finally, we discuss the role of quantum interference for training and decision making, paving the way for realizations of interpretable quantum learning agents.

Quantum machine learning beyond kernel methods

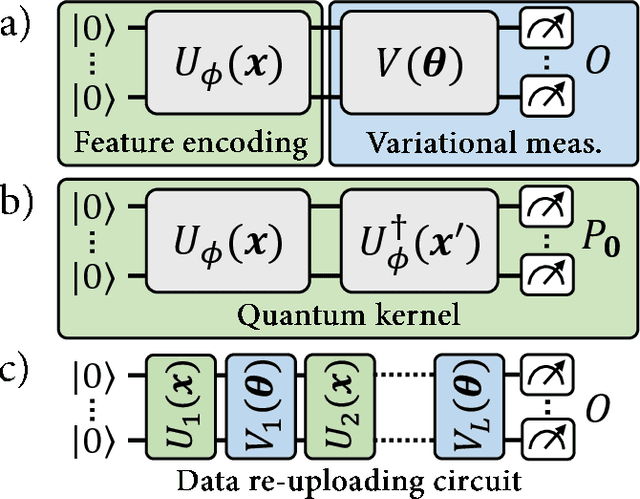
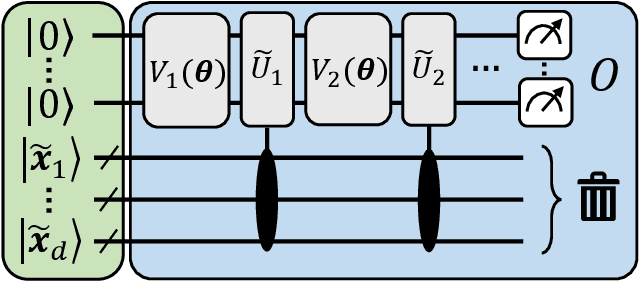
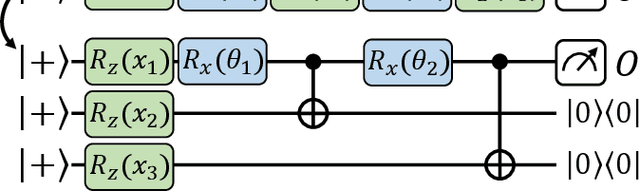
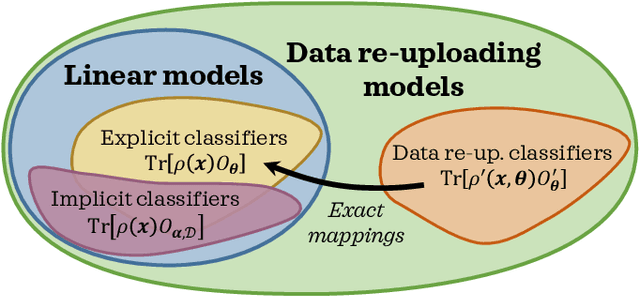
With noisy intermediate-scale quantum computers showing great promise for near-term applications, a number of machine learning algorithms based on parametrized quantum circuits have been suggested as possible means to achieve learning advantages. Yet, our understanding of how these quantum machine learning models compare, both to existing classical models and to each other, remains limited. A big step in this direction has been made by relating them to so-called kernel methods from classical machine learning. By building on this connection, previous works have shown that a systematic reformulation of many quantum machine learning models as kernel models was guaranteed to improve their training performance. In this work, we first extend the applicability of this result to a more general family of parametrized quantum circuit models called data re-uploading circuits. Secondly, we show, through simple constructions and numerical simulations, that models defined and trained variationally can exhibit a critically better generalization performance than their kernel formulations, which is the true figure of merit of machine learning tasks. Our results constitute another step towards a more comprehensive theory of quantum machine learning models next to kernel formulations.

Neural-Network Heuristics for Adaptive Bayesian Quantum Estimation

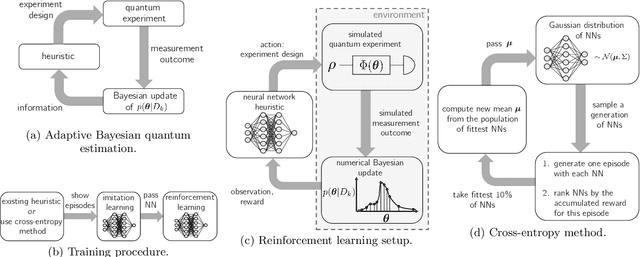
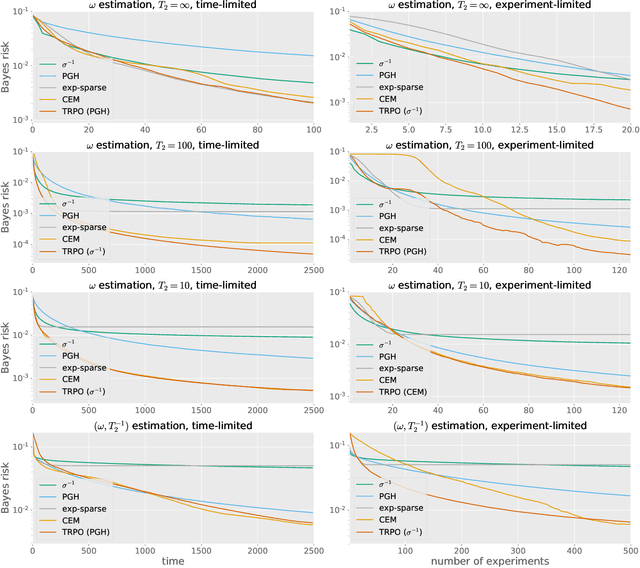
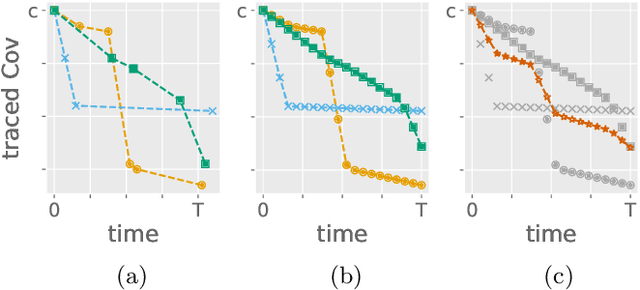
Quantum metrology promises unprecedented measurement precision but suffers in practice from the limited availability of resources such as the number of probes, their coherence time, or non-classical quantum states. The adaptive Bayesian approach to parameter estimation allows for an efficient use of resources thanks to adaptive experiment design. For its practical success fast numerical solutions for the Bayesian update and the adaptive experiment design are crucial. Here we show that neural networks can be trained to become fast and strong experiment-design heuristics using a combination of an evolutionary strategy and reinforcement learning. Neural-network heuristics are shown to outperform established heuristics for the technologically important example of frequency estimation of a qubit that suffers from dephasing. Our method of creating neural-network heuristics is very general and complements the well-studied sequential Monte-Carlo method for Bayesian updates to form a complete framework for adaptive Bayesian quantum estimation.

Improving the dynamics of quantum sensors with reinforcement learning

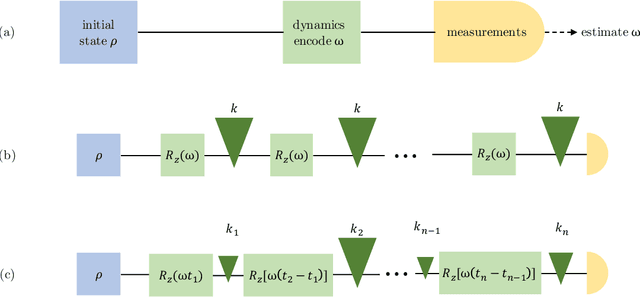
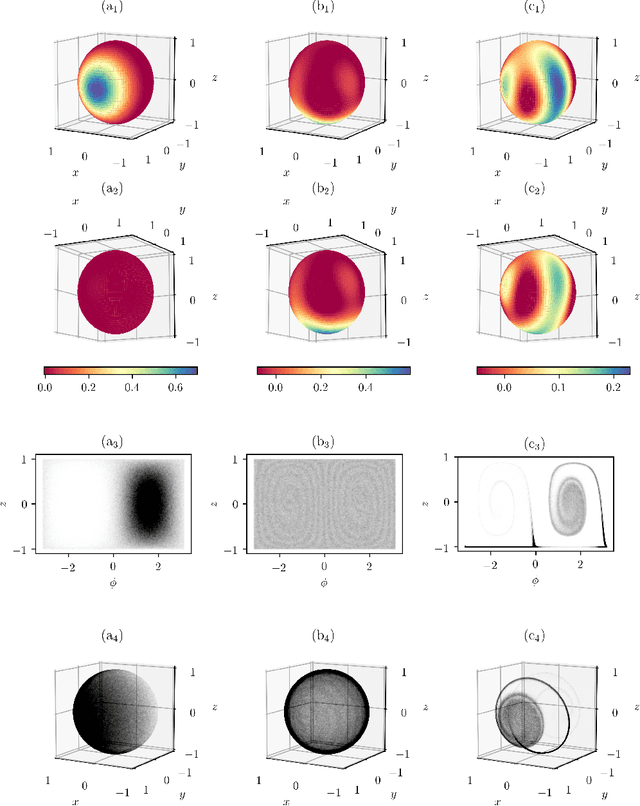
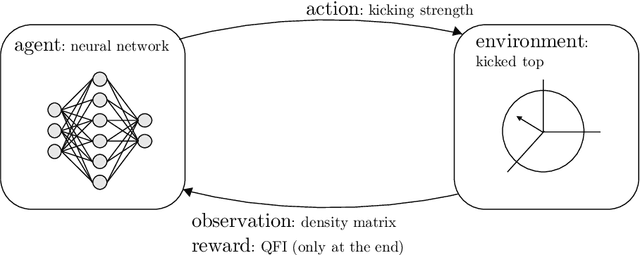
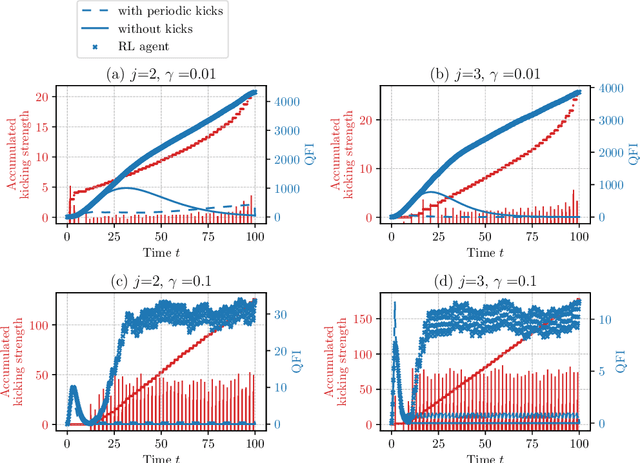
Recently proposed quantum-chaotic sensors achieve quantum enhancements in measurement precision by applying nonlinear control pulses to the dynamics of the quantum sensor while using classical initial states that are easy to prepare. Here, we use the cross entropy method of reinforcement learning to optimize the strength and position of control pulses. Compared to the quantum-chaotic sensors in the presence of superradiant damping, we find that decoherence can be fought even better and measurement precision can be enhanced further by optimizing the control. In some examples, we find enhancements in sensitivity by more than an order of magnitude. By visualizing the evolution of the quantum state, the mechanism exploited by the reinforcement learning method is identified as a kind of spin-squeezing strategy that is adapted to the superradiant damping.