Measurement-based quantum computation from Clifford quantum cellular automata

Measurement-based quantum computation (MBQC) is a paradigm for quantum computation where computation is driven by local measurements on a suitably entangled resource state. In this work we show that MBQC is related to a model of quantum computation based on Clifford quantum cellular automata (CQCA). Specifically, we show that certain MBQCs can be directly constructed from CQCAs which yields a simple and intuitive circuit model representation of MBQC in terms of quantum computation based on CQCA. We apply this description to construct various MBQC-based Ans\"atze for parameterized quantum circuits, demonstrating that the different Ans\"atze may lead to significantly different performances on different learning tasks. In this way, MBQC yields a family of Hardware-efficient Ans\"atze that may be adapted to specific problem settings and is particularly well suited for architectures with translationally invariant gates such as neutral atoms.

Variational measurement-based quantum computation for generative modeling

Measurement-based quantum computation (MBQC) offers a fundamentally unique paradigm to design quantum algorithms. Indeed, due to the inherent randomness of quantum measurements, the natural operations in MBQC are not deterministic and unitary, but are rather augmented with probabilistic byproducts. Yet, the main algorithmic use of MBQC so far has been to completely counteract this probabilistic nature in order to simulate unitary computations expressed in the circuit model. In this work, we propose designing MBQC algorithms that embrace this inherent randomness and treat the random byproducts in MBQC as a resource for computation. As a natural application where randomness can be beneficial, we consider generative modeling, a task in machine learning centered around generating complex probability distributions. To address this task, we propose a variational MBQC algorithm equipped with control parameters that allow to directly adjust the degree of randomness to be admitted in the computation. Our numerical findings indicate that this additional randomness can lead to significant gains in learning performance in certain generative modeling tasks. These results highlight the potential advantages in exploiting the inherent randomness of MBQC and motivate further research into MBQC-based algorithms.

Automated Gadget Discovery in Science

In recent years, reinforcement learning (RL) has become increasingly successful in its application to science and the process of scientific discovery in general. However, while RL algorithms learn to solve increasingly complex problems, interpreting the solutions they provide becomes ever more challenging. In this work, we gain insights into an RL agent's learned behavior through a post-hoc analysis based on sequence mining and clustering. Specifically, frequent and compact subroutines, used by the agent to solve a given task, are distilled as gadgets and then grouped by various metrics. This process of gadget discovery develops in three stages: First, we use an RL agent to generate data, then, we employ a mining algorithm to extract gadgets and finally, the obtained gadgets are grouped by a density-based clustering algorithm. We demonstrate our method by applying it to two quantum-inspired RL environments. First, we consider simulated quantum optics experiments for the design of high-dimensional multipartite entangled states where the algorithm finds gadgets that correspond to modern interferometer setups. Second, we consider a circuit-based quantum computing environment where the algorithm discovers various gadgets for quantum information processing, such as quantum teleportation. This approach for analyzing the policy of a learned agent is agent and environment agnostic and can yield interesting insights into any agent's policy.

Quantum machine learning beyond kernel methods

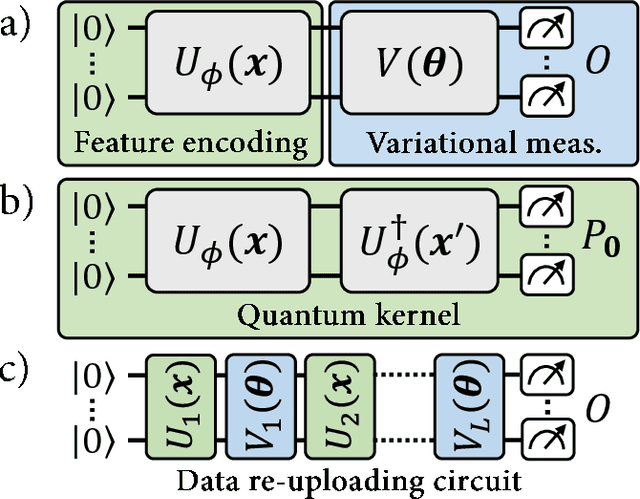
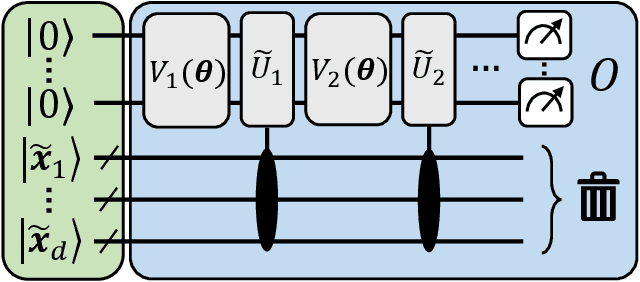
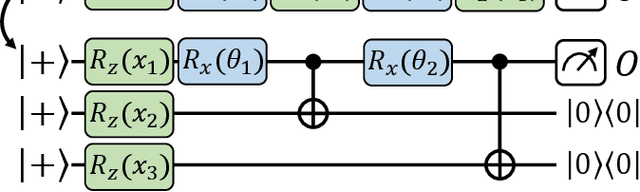
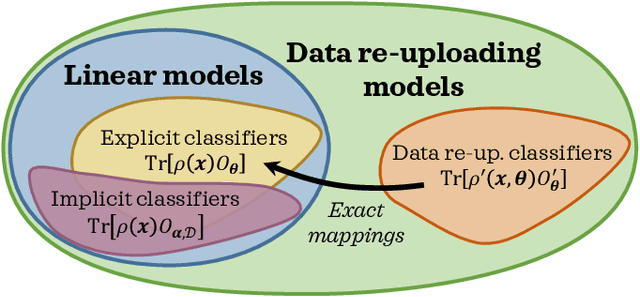
With noisy intermediate-scale quantum computers showing great promise for near-term applications, a number of machine learning algorithms based on parametrized quantum circuits have been suggested as possible means to achieve learning advantages. Yet, our understanding of how these quantum machine learning models compare, both to existing classical models and to each other, remains limited. A big step in this direction has been made by relating them to so-called kernel methods from classical machine learning. By building on this connection, previous works have shown that a systematic reformulation of many quantum machine learning models as kernel models was guaranteed to improve their training performance. In this work, we first extend the applicability of this result to a more general family of parametrized quantum circuit models called data re-uploading circuits. Secondly, we show, through simple constructions and numerical simulations, that models defined and trained variationally can exhibit a critically better generalization performance than their kernel formulations, which is the true figure of merit of machine learning tasks. Our results constitute another step towards a more comprehensive theory of quantum machine learning models next to kernel formulations.

Operationally meaningful representations of physical systems in neural networks

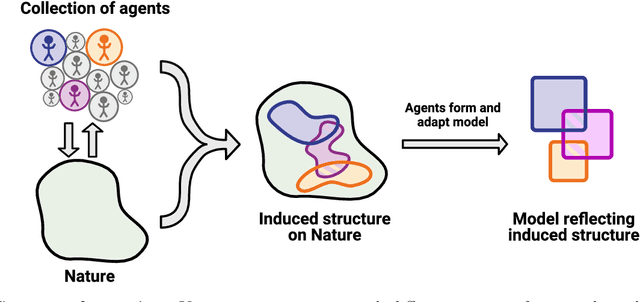
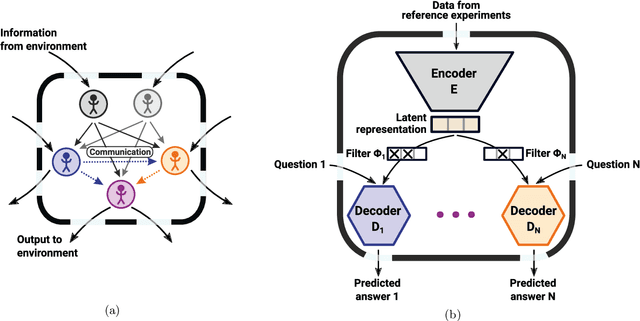
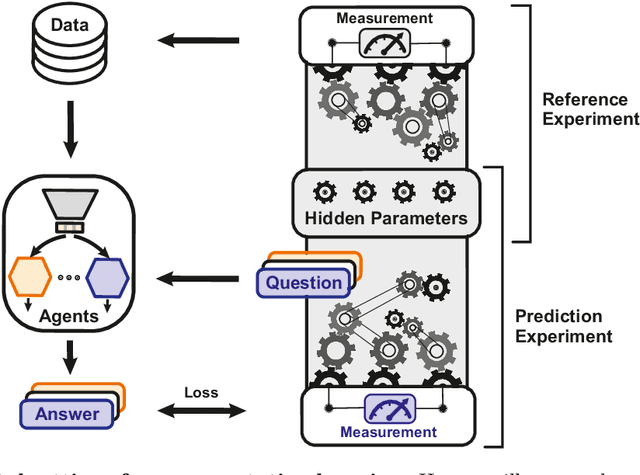
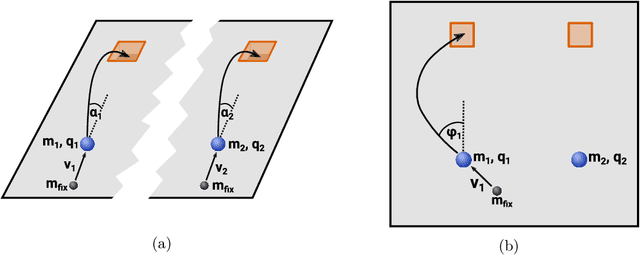
To make progress in science, we often build abstract representations of physical systems that meaningfully encode information about the systems. The representations learnt by most current machine learning techniques reflect statistical structure present in the training data; however, these methods do not allow us to specify explicit and operationally meaningful requirements on the representation. Here, we present a neural network architecture based on the notion that agents dealing with different aspects of a physical system should be able to communicate relevant information as efficiently as possible to one another. This produces representations that separate different parameters which are useful for making statements about the physical system in different experimental settings. We present examples involving both classical and quantum physics. For instance, our architecture finds a compact representation of an arbitrary two-qubit system that separates local parameters from parameters describing quantum correlations. We further show that this method can be combined with reinforcement learning to enable representation learning within interactive scenarios where agents need to explore experimental settings to identify relevant variables.

A framework for deep energy-based reinforcement learning with quantum speed-up

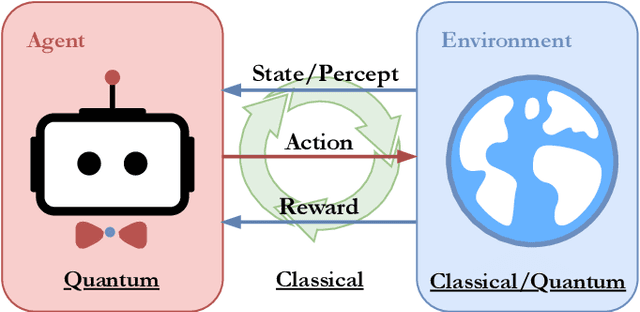
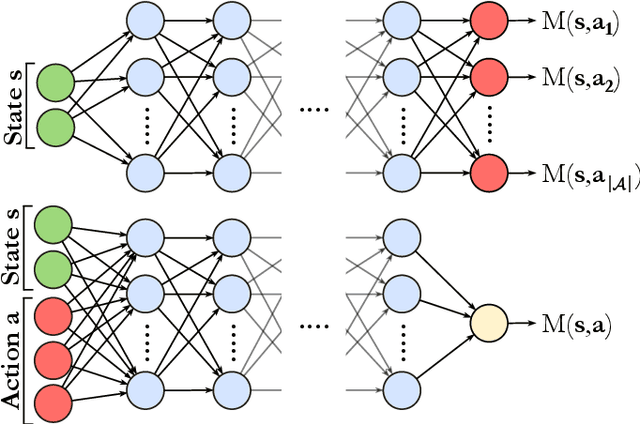
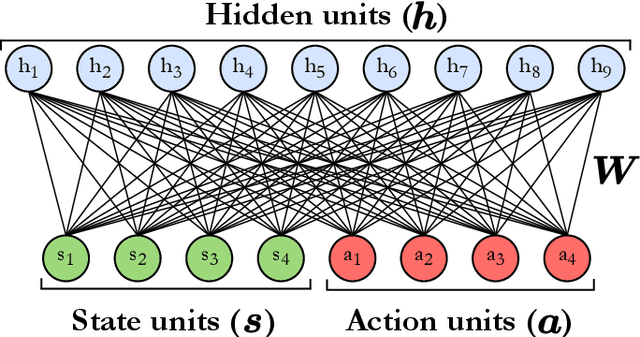
In the past decade, deep learning methods have seen tremendous success in various supervised and unsupervised learning tasks such as classification and generative modeling. More recently, deep neural networks have emerged in the domain of reinforcement learning as a tool to solve decision-making problems of unprecedented complexity, e.g., navigation problems or game-playing AI. Despite the successful combinations of ideas from quantum computing with machine learning methods, there have been relatively few attempts to design quantum algorithms that would enhance deep reinforcement learning. This is partly due to the fact that quantum enhancements of deep neural networks, in general, have not been as extensively investigated as other quantum machine learning methods. In contrast, projective simulation is a reinforcement learning model inspired by the stochastic evolution of physical systems that enables a quantum speed-up in decision making. In this paper, we develop a unifying framework that connects deep learning and projective simulation, opening the route to quantum improvements in deep reinforcement learning. Our approach is based on so-called generative energy-based models to design reinforcement learning methods with a computational advantage in solving complex and large-scale decision-making problems.

Photonic architecture for reinforcement learning

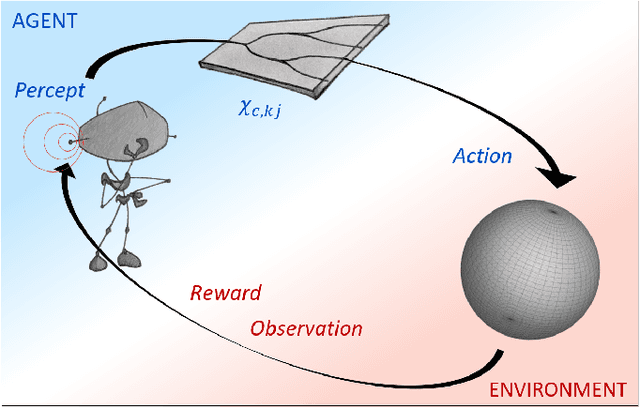
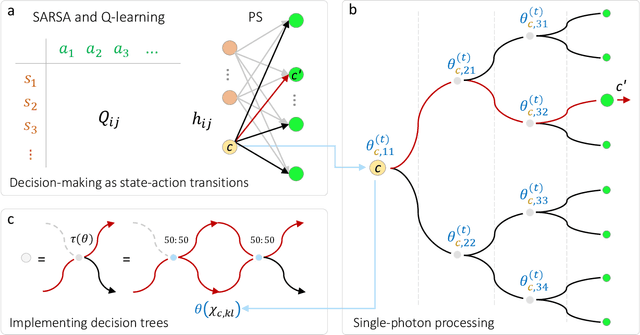
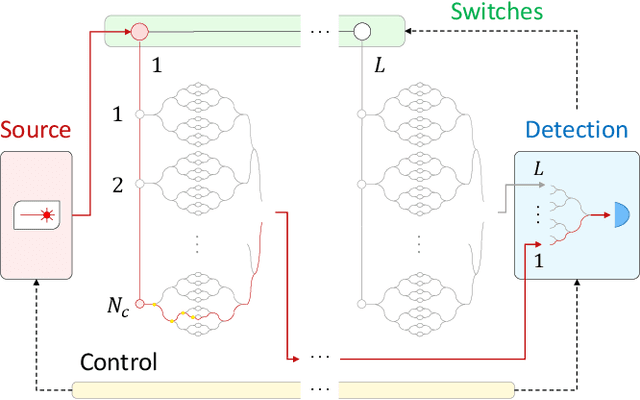
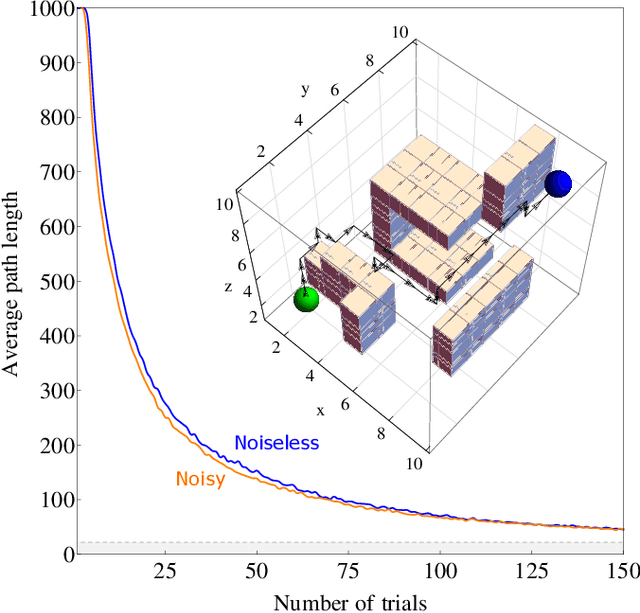
The last decade has seen an unprecedented growth in artificial intelligence and photonic technologies, both of which drive the limits of modern-day computing devices. In line with these recent developments, this work brings together the state of the art of both fields within the framework of reinforcement learning. We present the blueprint for a photonic implementation of an active learning machine incorporating contemporary algorithms such as SARSA, Q-learning, and projective simulation. We numerically investigate its performance within typical reinforcement learning environments, showing that realistic levels of experimental noise can be tolerated or even be beneficial for the learning process. Remarkably, the architecture itself enables mechanisms of abstraction and generalization, two features which are often considered key ingredients for artificial intelligence. The proposed architecture, based on single-photon evolution on a mesh of tunable beamsplitters, is simple, scalable, and a first integration in portable systems appears to be within the reach of near-term technology.

Optimizing Quantum Error Correction Codes with Reinforcement Learning

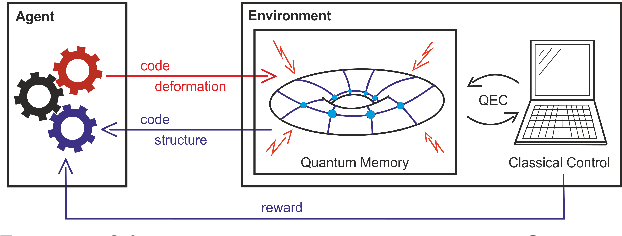
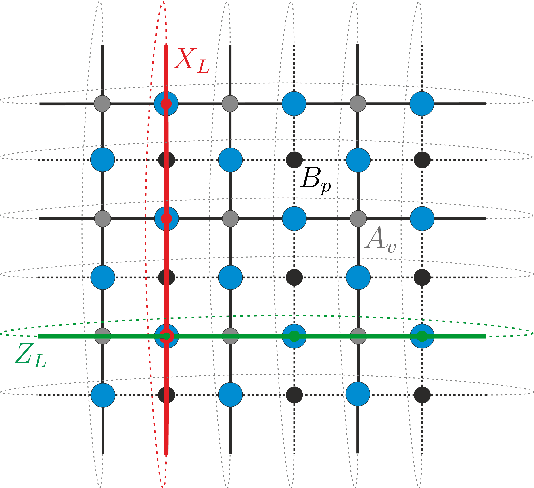
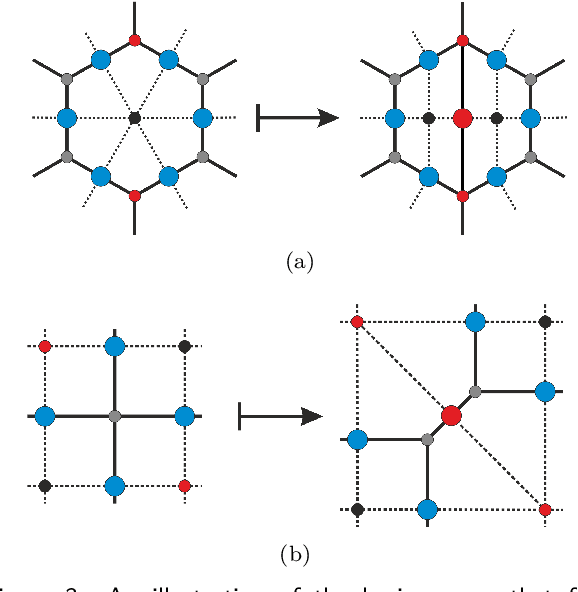
Quantum error correction is widely thought to be the key to fault-tolerant quantum computation. However, determining the most suited encoding for unknown error channels or specific laboratory setups is highly challenging. Here, we present a reinforcement learning framework for optimizing and fault-tolerantly adapting quantum error correction codes. We consider a reinforcement learning agent tasked with modifying a quantum memory until a desired logical error rate is reached. Using efficient simulations of a surface code quantum memory with about 70 physical qubits, we demonstrate that such a reinforcement learning agent can determine near-optimal solutions, in terms of the number of physical qubits, for various error models of interest. Moreover, we show that agents trained on one task are able to transfer their experience to similar tasks. This ability for transfer learning showcases the inherent strengths of reinforcement learning and the applicability of our approach for optimization both in off-line simulations and on-line under laboratory conditions.

Active learning machine learns to create new quantum experiments

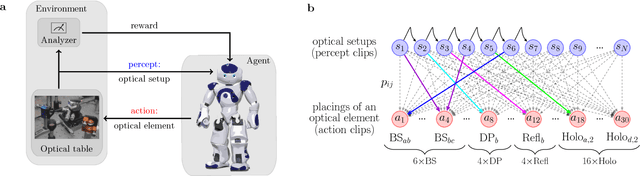
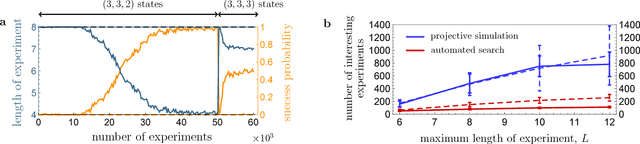
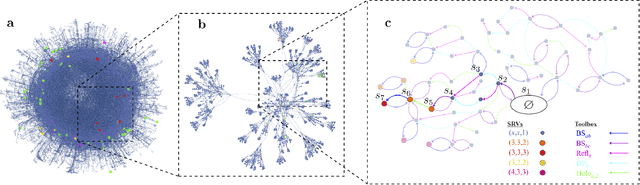
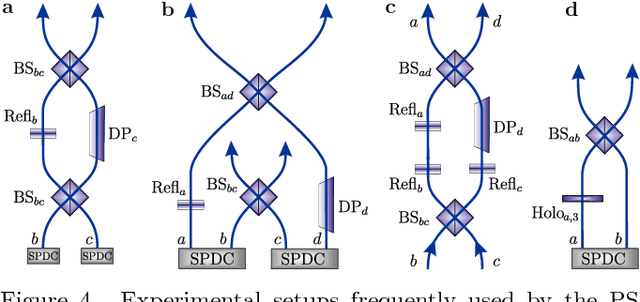
How useful can machine learning be in a quantum laboratory? Here we raise the question of the potential of intelligent machines in the context of scientific research. A major motivation for the present work is the unknown reachability of various entanglement classes in quantum experiments. We investigate this question by using the projective simulation model, a physics-oriented approach to artificial intelligence. In our approach, the projective simulation system is challenged to design complex photonic quantum experiments that produce high-dimensional entangled multiphoton states, which are of high interest in modern quantum experiments. The artificial intelligence system learns to create a variety of entangled states, and improves the efficiency of their realization. In the process, the system autonomously (re)discovers experimental techniques which are only now becoming standard in modern quantum optical experiments - a trait which was not explicitly demanded from the system but emerged through the process of learning. Such features highlight the possibility that machines could have a significantly more creative role in future research.