Optimizing Quantum Error Correction Codes with Reinforcement Learning

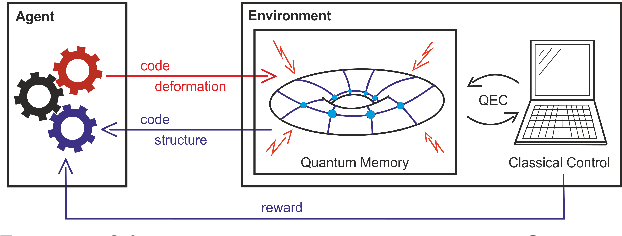
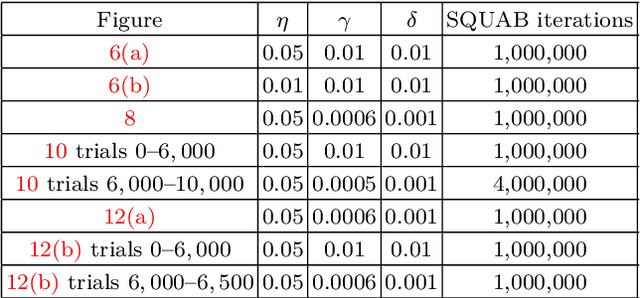
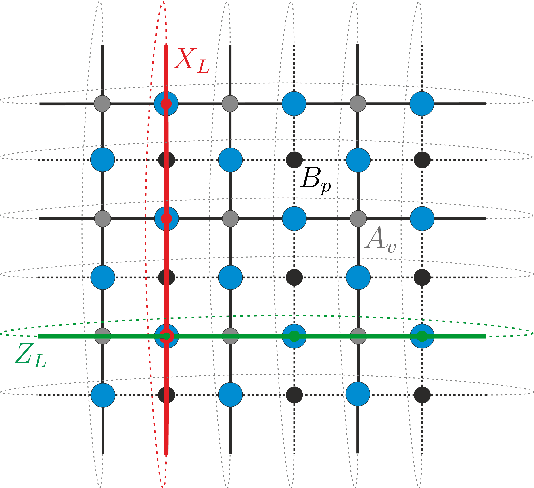
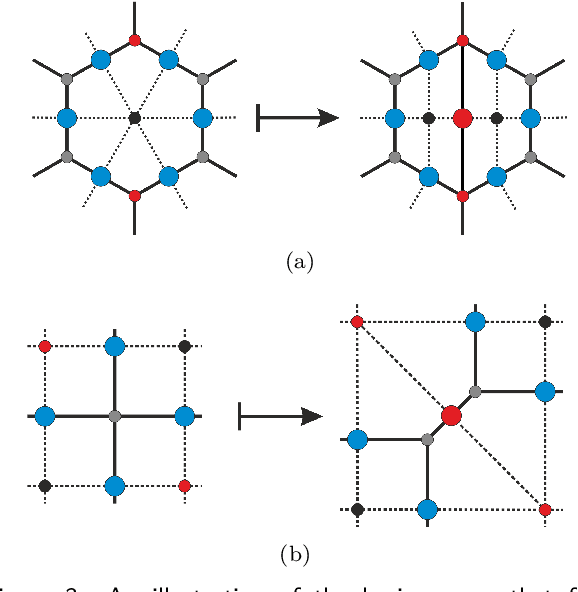
Quantum error correction is widely thought to be the key to fault-tolerant quantum computation. However, determining the most suited encoding for unknown error channels or specific laboratory setups is highly challenging. Here, we present a reinforcement learning framework for optimizing and fault-tolerantly adapting quantum error correction codes. We consider a reinforcement learning agent tasked with modifying a quantum memory until a desired logical error rate is reached. Using efficient simulations of a surface code quantum memory with about 70 physical qubits, we demonstrate that such a reinforcement learning agent can determine near-optimal solutions, in terms of the number of physical qubits, for various error models of interest. Moreover, we show that agents trained on one task are able to transfer their experience to similar tasks. This ability for transfer learning showcases the inherent strengths of reinforcement learning and the applicability of our approach for optimization both in off-line simulations and on-line under laboratory conditions.

Speeding-up the decision making of a learning agent using an ion trap quantum processor

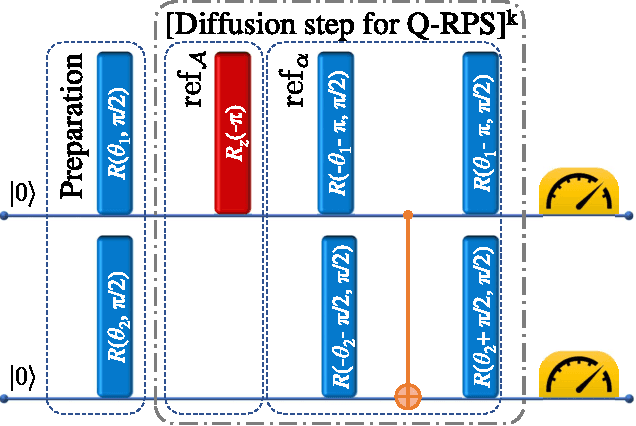
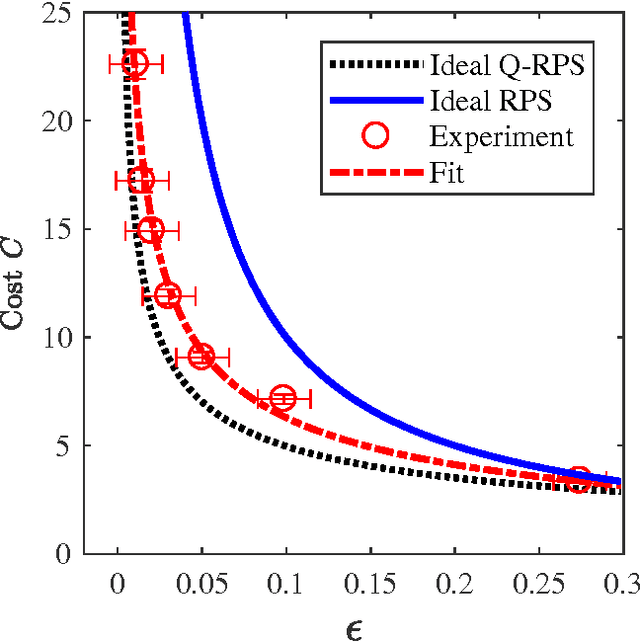
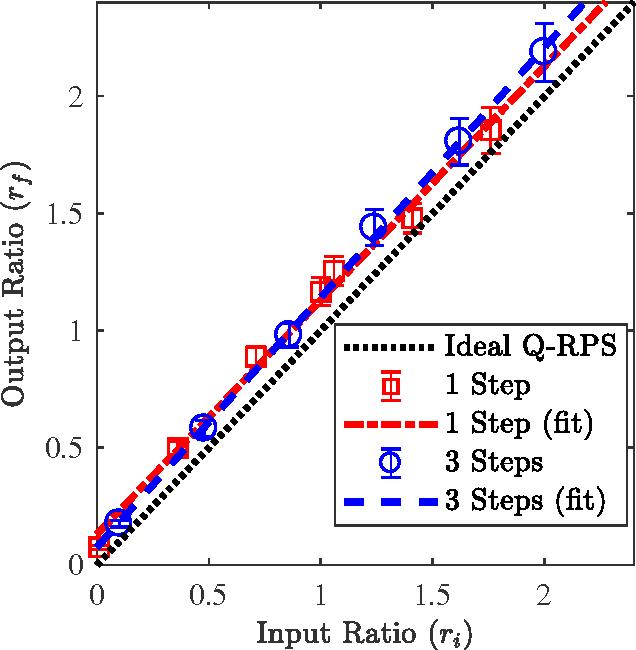
We report a proof-of-principle experimental demonstration of the quantum speed-up for learning agents utilizing a small-scale quantum information processor based on radiofrequency-driven trapped ions. The decision-making process of a quantum learning agent within the projective simulation paradigm for machine learning is implemented in a system of two qubits. The latter are realized using hyperfine states of two frequency-addressed atomic ions exposed to a static magnetic field gradient. We show that the deliberation time of this quantum learning agent is quadratically improved with respect to comparable classical learning agents. The performance of this quantum-enhanced learning agent highlights the potential of scalable quantum processors taking advantage of machine learning.