Q-Match: Iterative Shape Matching via Quantum Annealing

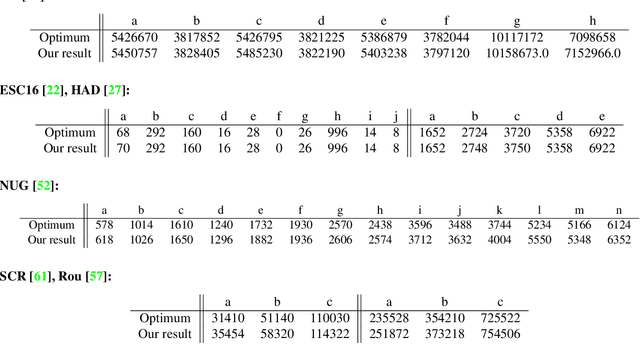
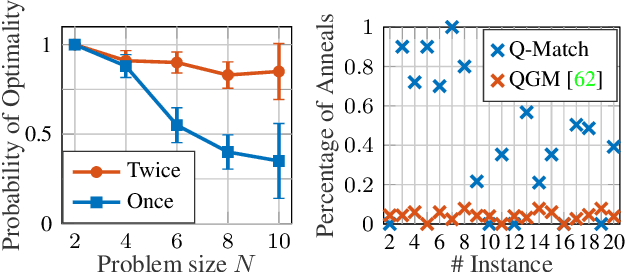
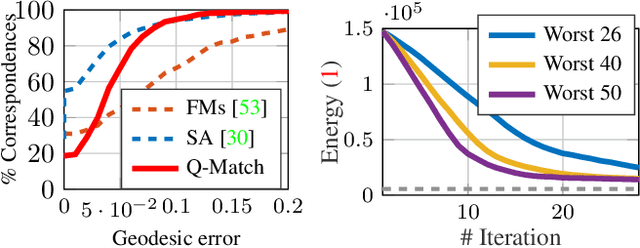
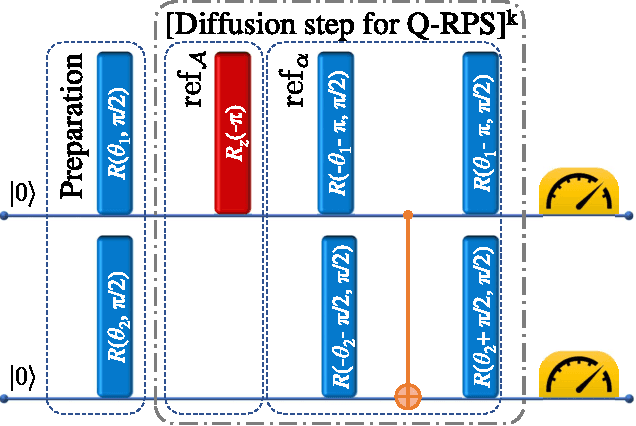
Finding shape correspondences can be formulated as an NP-hard quadratic assignment problem (QAP) that becomes infeasible for shapes with high sampling density. A promising research direction is to tackle such quadratic optimization problems over binary variables with quantum annealing, which, in theory, allows to find globally optimal solutions relying on a new computational paradigm. Unfortunately, enforcing the linear equality constraints in QAPs via a penalty significantly limits the success probability of such methods on currently available quantum hardware. To address this limitation, this paper proposes Q-Match, i.e., a new iterative quantum method for QAPs inspired by the alpha-expansion algorithm, which allows solving problems of an order of magnitude larger than current quantum methods. It works by implicitly enforcing the QAP constraints by updating the current estimates in a cyclic fashion. Further, Q-Match can be applied for shape matching problems iteratively, on a subset of well-chosen correspondences, allowing us to scale to real-world problems. Using the latest quantum annealer, the D-Wave Advantage, we evaluate the proposed method on a subset of QAPLIB as well as on isometric shape matching problems from the FAUST dataset.

Speeding-up the decision making of a learning agent using an ion trap quantum processor

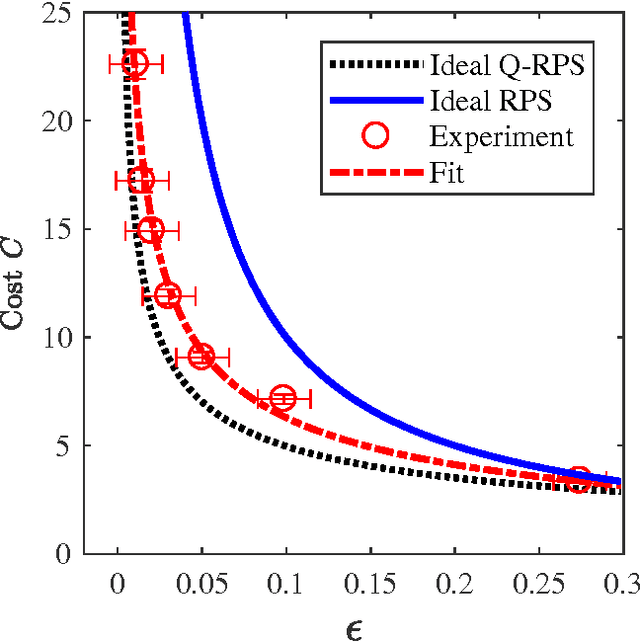
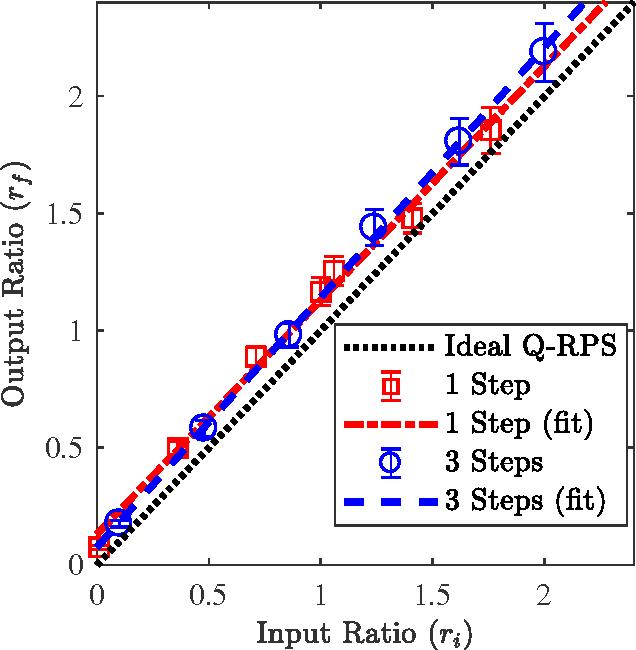
We report a proof-of-principle experimental demonstration of the quantum speed-up for learning agents utilizing a small-scale quantum information processor based on radiofrequency-driven trapped ions. The decision-making process of a quantum learning agent within the projective simulation paradigm for machine learning is implemented in a system of two qubits. The latter are realized using hyperfine states of two frequency-addressed atomic ions exposed to a static magnetic field gradient. We show that the deliberation time of this quantum learning agent is quadratically improved with respect to comparable classical learning agents. The performance of this quantum-enhanced learning agent highlights the potential of scalable quantum processors taking advantage of machine learning.