Disentanglement by means of action-induced representations

Learning interpretable representations with variational autoencoders (VAEs) is a major goal of representation learning. The main challenge lies in obtaining disentangled representations, where each latent dimension corresponds to a distinct generative factor. This difficulty is fundamentally tied to the inability to perform nonlinear independent component analysis. Here, we introduce the framework of action-induced representations (AIRs) which models representations of physical systems given experiments (or actions) that can be performed on them. We show that, in this framework, we can provably disentangle degrees of freedom w.r.t. their action dependence. We further introduce a variational AIR architecture (VAIR) that can extract AIRs and therefore achieve provable disentanglement where standard VAEs fail. Beyond state representation, VAIR also captures the action dependence of the underlying generative factors, directly linking experiments to the degrees of freedom they influence.

The Work Capacity of Channels with Memory: Maximum Extractable Work in Percept-Action Loops

Predicting future observations plays a central role in machine learning, biology, economics, and many other fields. It lies at the heart of organizational principles such as the variational free energy principle and has even been shown -- based on the second law of thermodynamics -- to be necessary for reaching the fundamental energetic limits of sequential information processing. While the usefulness of the predictive paradigm is undisputed, complex adaptive systems that interact with their environment are more than just predictive machines: they have the power to act upon their environment and cause change. In this work, we develop a framework to analyze the thermodynamics of information processing in percept-action loops -- a model of agent-environment interaction -- allowing us to investigate the thermodynamic implications of actions and percepts on equal footing. To this end, we introduce the concept of work capacity -- the maximum rate at which an agent can expect to extract work from its environment. Our results reveal that neither of two previously established design principles for work-efficient agents -- maximizing predictive power and forgetting past actions -- remains optimal in environments where actions have observable consequences. Instead, a trade-off emerges: work-efficient agents must balance prediction and forgetting, as remembering past actions can reduce the available free energy. This highlights a fundamental departure from the thermodynamics of passive observation, suggesting that prediction and energy efficiency may be at odds in active learning systems.

Learning to reset in target search problems

Target search problems are central to a wide range of fields, from biological foraging to the optimization algorithms. Recently, the ability to reset the search has been shown to significantly improve the searcher's efficiency. However, the optimal resetting strategy depends on the specific properties of the search problem and can often be challenging to determine. In this work, we propose a reinforcement learning (RL)-based framework to train agents capable of optimizing their search efficiency in environments by learning how to reset. First, we validate the approach in a well-established benchmark: the Brownian search with resetting. There, RL agents consistently recover strategies closely resembling the sharp resetting distribution, known to be optimal in this scenario. We then extend the framework by allowing agents to control not only when to reset, but also their spatial dynamics through turning actions. In this more complex setting, the agents discover strategies that adapt both resetting and turning to the properties of the environment, outperforming the proposed benchmarks. These results demonstrate how reinforcement learning can serve both as an optimization tool and a mechanism for uncovering new, interpretable strategies in stochastic search processes with resetting.

Free Energy Projective Simulation (FEPS): Active inference with interpretability

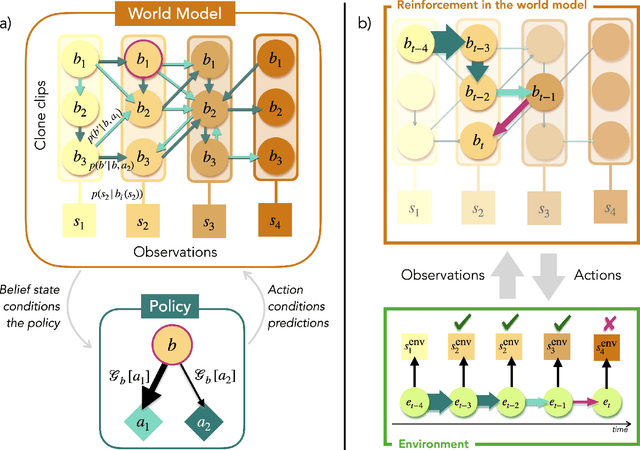
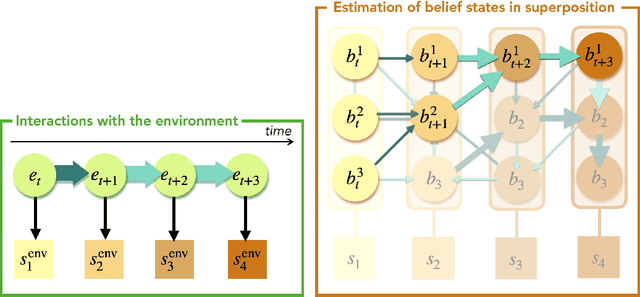
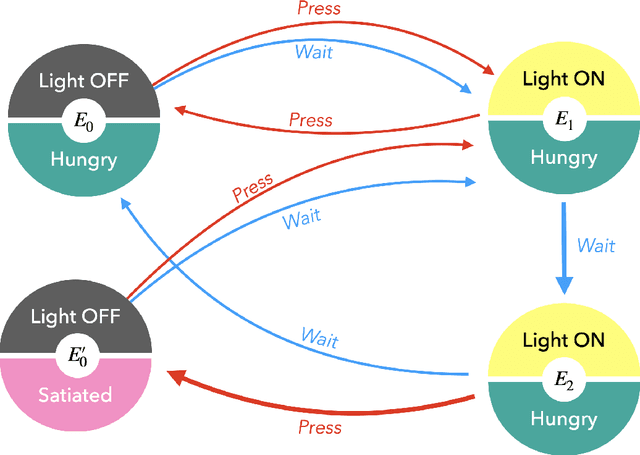
In the last decade, the free energy principle (FEP) and active inference (AIF) have achieved many successes connecting conceptual models of learning and cognition to mathematical models of perception and action. This effort is driven by a multidisciplinary interest in understanding aspects of self-organizing complex adaptive systems, including elements of agency. Various reinforcement learning (RL) models performing active inference have been proposed and trained on standard RL tasks using deep neural networks. Recent work has focused on improving such agents' performance in complex environments by incorporating the latest machine learning techniques. In this paper, we take an alternative approach. Within the constraints imposed by the FEP and AIF, we attempt to model agents in an interpretable way without deep neural networks by introducing Free Energy Projective Simulation (FEPS). Using internal rewards only, FEPS agents build a representation of their partially observable environments with which they interact. Following AIF, the policy to achieve a given task is derived from this world model by minimizing the expected free energy. Leveraging the interpretability of the model, techniques are introduced to deal with long-term goals and reduce prediction errors caused by erroneous hidden state estimation. We test the FEPS model on two RL environments inspired from behavioral biology: a timed response task and a navigation task in a partially observable grid. Our results show that FEPS agents fully resolve the ambiguity of both environments by appropriately contextualizing their observations based on prediction accuracy only. In addition, they infer optimal policies flexibly for any target observation in the environment.

A Universal Quantum Computer From Relativistic Motion

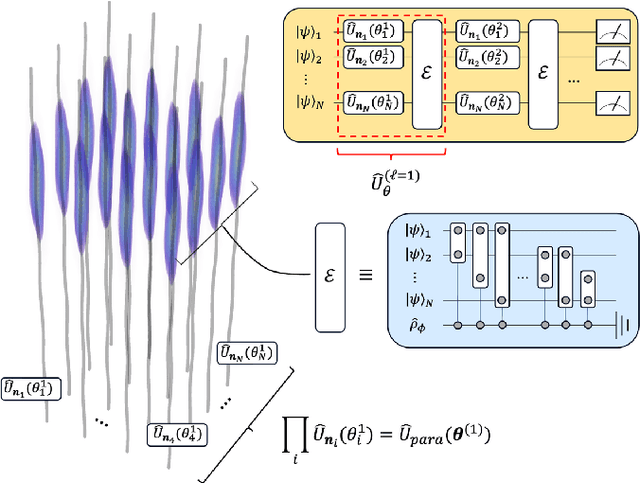
We present an explicit construction of a relativistic quantum computing architecture using a variational quantum circuit approach that is shown to allow for universal quantum computing. The variational quantum circuit consists of tunable single-qubit rotations and entangling gates that are implemented successively. The single qubit rotations are parameterized by the proper time intervals of the qubits' trajectories and can be tuned by varying their relativistic motion in spacetime. The entangling layer is mediated by a relativistic quantum field instead of through direct coupling between the qubits. Within this setting, we give a prescription for how to use quantum field-mediated entanglement and manipulation of the relativistic motion of qubits to obtain a universal gate set, for which compact non-perturbative expressions that are valid for general spacetimes are also obtained. We also derive a lower bound on the channel fidelity that shows the existence of parameter regimes in which all entangling operations are effectively unitary, despite the noise generated from the presence of a mediating quantum field. Finally, we consider an explicit implementation of the quantum Fourier transform with relativistic qubits.

Multi-Excitation Projective Simulation with a Many-Body Physics Inspired Inductive Bias

With the impressive progress of deep learning, applications relying on machine learning are increasingly being integrated into daily life. However, most deep learning models have an opaque, oracle-like nature making it difficult to interpret and understand their decisions. This problem led to the development of the field known as eXplainable Artificial Intelligence (XAI). One method in this field known as Projective Simulation (PS) models a chain-of-thought as a random walk of a particle on a graph with vertices that have concepts attached to them. While this description has various benefits, including the possibility of quantization, it cannot be naturally used to model thoughts that combine several concepts simultaneously. To overcome this limitation, we introduce Multi-Excitation Projective Simulation (mePS), a generalization that considers a chain-of-thought to be a random walk of several particles on a hypergraph. A definition for a dynamic hypergraph is put forward to describe the agent's training history along with applications to AI and hypergraph visualization. An inductive bias inspired by the remarkably successful few-body interaction models used in quantum many-body physics is formalized for our classical mePS framework and employed to tackle the exponential complexity associated with naive implementations of hypergraphs. We prove that our inductive bias reduces the complexity from exponential to polynomial, with the exponent representing the cutoff on how many particles can interact. We numerically apply our method to two toy environments and a more complex scenario modelling the diagnosis of a broken computer. These environments demonstrate the resource savings provided by an appropriate choice of inductive bias, as well as showcasing aspects of interpretability. A quantum model for mePS is also briefly outlined and some future directions for it are discussed.

Measurement-based quantum computation from Clifford quantum cellular automata

Measurement-based quantum computation (MBQC) is a paradigm for quantum computation where computation is driven by local measurements on a suitably entangled resource state. In this work we show that MBQC is related to a model of quantum computation based on Clifford quantum cellular automata (CQCA). Specifically, we show that certain MBQCs can be directly constructed from CQCAs which yields a simple and intuitive circuit model representation of MBQC in terms of quantum computation based on CQCA. We apply this description to construct various MBQC-based Ans\"atze for parameterized quantum circuits, demonstrating that the different Ans\"atze may lead to significantly different performances on different learning tasks. In this way, MBQC yields a family of Hardware-efficient Ans\"atze that may be adapted to specific problem settings and is particularly well suited for architectures with translationally invariant gates such as neutral atoms.

Quantum circuit synthesis with diffusion models

Quantum computing has recently emerged as a transformative technology. Yet, its promised advantages rely on efficiently translating quantum operations into viable physical realizations. In this work, we use generative machine learning models, specifically denoising diffusion models (DMs), to facilitate this transformation. Leveraging text-conditioning, we steer the model to produce desired quantum operations within gate-based quantum circuits. Notably, DMs allow to sidestep during training the exponential overhead inherent in the classical simulation of quantum dynamics -- a consistent bottleneck in preceding ML techniques. We demonstrate the model's capabilities across two tasks: entanglement generation and unitary compilation. The model excels at generating new circuits and supports typical DM extensions such as masking and editing to, for instance, align the circuit generation to the constraints of the targeted quantum device. Given their flexibility and generalization abilities, we envision DMs as pivotal in quantum circuit synthesis, enhancing both practical applications but also insights into theoretical quantum computation.

Variational measurement-based quantum computation for generative modeling

Measurement-based quantum computation (MBQC) offers a fundamentally unique paradigm to design quantum algorithms. Indeed, due to the inherent randomness of quantum measurements, the natural operations in MBQC are not deterministic and unitary, but are rather augmented with probabilistic byproducts. Yet, the main algorithmic use of MBQC so far has been to completely counteract this probabilistic nature in order to simulate unitary computations expressed in the circuit model. In this work, we propose designing MBQC algorithms that embrace this inherent randomness and treat the random byproducts in MBQC as a resource for computation. As a natural application where randomness can be beneficial, we consider generative modeling, a task in machine learning centered around generating complex probability distributions. To address this task, we propose a variational MBQC algorithm equipped with control parameters that allow to directly adjust the degree of randomness to be admitted in the computation. Our numerical findings indicate that this additional randomness can lead to significant gains in learning performance in certain generative modeling tasks. These results highlight the potential advantages in exploiting the inherent randomness of MBQC and motivate further research into MBQC-based algorithms.

Optimal foraging strategies can be learned and outperform Lévy walks

L\'evy walks and other theoretical models of optimal foraging have been successfully used to describe real-world scenarios, attracting attention in several fields such as economy, physics, ecology, and evolutionary biology. However, it remains unclear in most cases which strategies maximize foraging efficiency and whether such strategies can be learned by living organisms. To address these questions, we model foragers as reinforcement learning agents. We first prove theoretically that maximizing rewards in our reinforcement learning model is equivalent to optimizing foraging efficiency. We then show with numerical experiments that our agents learn foraging strategies which outperform the efficiency of known strategies such as L\'evy walks.