Artificial Agency and Large Language Models

The arrival of Large Language Models (LLMs) has stirred up philosophical debates about the possibility of realizing agency in an artificial manner. In this work we contribute to the debate by presenting a theoretical model that can be used as a threshold conception for artificial agents. The model defines agents as systems whose actions and goals are always influenced by a dynamic framework of factors that consists of the agent's accessible history, its adaptive repertoire and its external environment. This framework, in turn, is influenced by the actions that the agent takes and the goals that it forms. We show with the help of the model that state-of-the-art LLMs are not agents yet, but that there are elements to them that suggest a way forward. The paper argues that a combination of the agent architecture presented in Park et al. (2023) together with the use of modules like the Coscientist in Boiko et al. (2023) could potentially be a way to realize agency in an artificial manner. We end the paper by reflecting on the obstacles one might face in building such an artificial agent and by presenting possible directions for future research.

Quantum circuit synthesis with diffusion models

Quantum computing has recently emerged as a transformative technology. Yet, its promised advantages rely on efficiently translating quantum operations into viable physical realizations. In this work, we use generative machine learning models, specifically denoising diffusion models (DMs), to facilitate this transformation. Leveraging text-conditioning, we steer the model to produce desired quantum operations within gate-based quantum circuits. Notably, DMs allow to sidestep during training the exponential overhead inherent in the classical simulation of quantum dynamics -- a consistent bottleneck in preceding ML techniques. We demonstrate the model's capabilities across two tasks: entanglement generation and unitary compilation. The model excels at generating new circuits and supports typical DM extensions such as masking and editing to, for instance, align the circuit generation to the constraints of the targeted quantum device. Given their flexibility and generalization abilities, we envision DMs as pivotal in quantum circuit synthesis, enhancing both practical applications but also insights into theoretical quantum computation.

Universal representation by Boltzmann machines with Regularised Axons

It is widely known that Boltzmann machines are capable of representing arbitrary probability distributions over the values of their visible neurons, given enough hidden ones. However, sampling -- and thus training -- these models can be numerically hard. Recently we proposed a regularisation of the connections of Boltzmann machines, in order to control the energy landscape of the model, paving a way for efficient sampling and training. Here we formally prove that such regularised Boltzmann machines preserve the ability to represent arbitrary distributions. This is in conjunction with controlling the number of energy local minima, thus enabling easy \emph{guided} sampling and training. Furthermore, we explicitly show that regularised Boltzmann machines can store exponentially many arbitrarily correlated visible patterns with perfect retrieval, and we connect them to the Dense Associative Memory networks.

Learning minimal representations of stochastic processes with variational autoencoders

Stochastic processes have found numerous applications in science, as they are broadly used to model a variety of natural phenomena. Due to their intrinsic randomness and uncertainty, they are however difficult to characterize. Here, we introduce an unsupervised machine learning approach to determine the minimal set of parameters required to effectively describe the dynamics of a stochastic process. Our method builds upon an extended $\beta$-variational autoencoder architecture. By means of simulated datasets corresponding to paradigmatic diffusion models, we showcase its effectiveness in extracting the minimal relevant parameters that accurately describe these dynamics. Furthermore, the method enables the generation of new trajectories that faithfully replicate the expected stochastic behavior. Overall, our approach enables for the autonomous discovery of unknown parameters describing stochastic processes, hence enhancing our comprehension of complex phenomena across various fields.

Optimal foraging strategies can be learned and outperform Lévy walks

L\'evy walks and other theoretical models of optimal foraging have been successfully used to describe real-world scenarios, attracting attention in several fields such as economy, physics, ecology, and evolutionary biology. However, it remains unclear in most cases which strategies maximize foraging efficiency and whether such strategies can be learned by living organisms. To address these questions, we model foragers as reinforcement learning agents. We first prove theoretically that maximizing rewards in our reinforcement learning model is equivalent to optimizing foraging efficiency. We then show with numerical experiments that our agents learn foraging strategies which outperform the efficiency of known strategies such as L\'evy walks.

Preface: Characterisation of Physical Processes from Anomalous Diffusion Data

Preface to the special issue "Characterisation of Physical Processes from Anomalous Diffusion Data" associated with the Anomalous Diffusion Challenge ( https://andi-challenge.org ) and published in Journal of Physics A: Mathematical and Theoretical. The list of articles included in the special issue can be accessed at https://iopscience.iop.org/journal/1751-8121/page/Characterisation-of-Physical-Processes-from-Anomalous-Diffusion-Data .

Unsupervised learning of anomalous diffusion data

The characterization of diffusion processes is a keystone in our understanding of a variety of physical phenomena. Many of these deviate from Brownian motion, giving rise to anomalous diffusion. Various theoretical models exists nowadays to describe such processes, but their application to experimental setups is often challenging, due to the stochastic nature of the phenomena and the difficulty to harness reliable data. The latter often consists on short and noisy trajectories, which are hard to characterize with usual statistical approaches. In recent years, we have witnessed an impressive effort to bridge theory and experiments by means of supervised machine learning techniques, with astonishing results. In this work, we explore the use of unsupervised methods in anomalous diffusion data. We show that the main diffusion characteristics can be learnt without the need of any labelling of the data. We use such method to discriminate between anomalous diffusion models and extract their physical parameters. Moreover, we explore the feasibility of finding novel types of diffusion, in this case represented by compositions of existing diffusion models. At last, we showcase the use of the method in experimental data and demonstrate its advantages for cases where supervised learning is not applicable.

Efficient training of energy-based models via spin-glass control

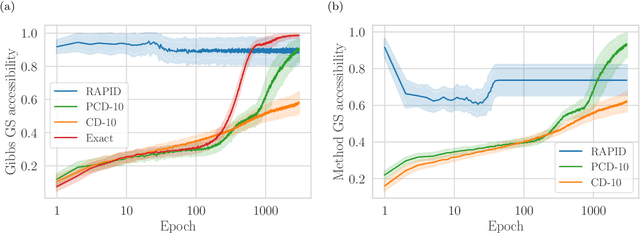
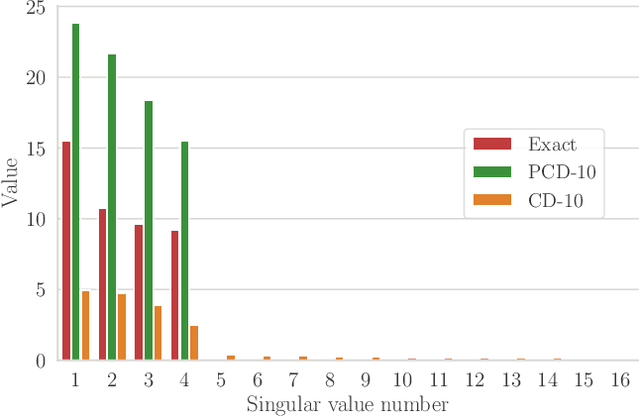
We present an efficient method for unsupervised learning using Boltzmann machines. The method is rooted in the control of the spin-glass properties of the Ising model described by the Boltzmann machine's weights. This allows for very easy access to low-energy configurations. We apply RAPID, the combination of Restricting the Axons (RA) of the model and training via Pattern-InDuced correlations (PID), to learn the Bars and Stripes dataset of various sizes and the MNIST dataset. We show how, in these tasks, RAPID quickly outperforms standard techniques for unsupervised learning in generalization ability. Indeed, both the number of epochs needed for effective learning and the computation time per training step are greatly reduced. In its simplest form, PID allows to compute the negative phase of the log-likelihood gradient with no Markov chain Monte Carlo sampling costs at all.

Machine learning method for single trajectory characterization

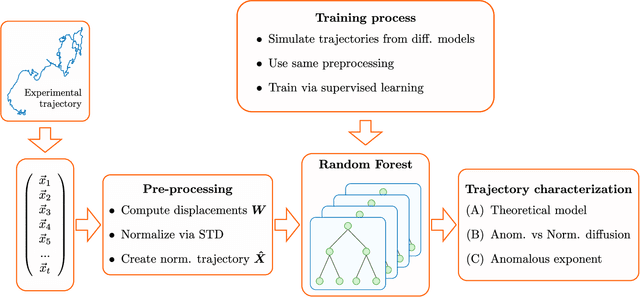
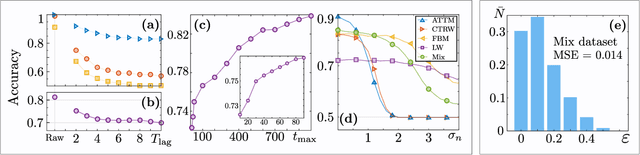
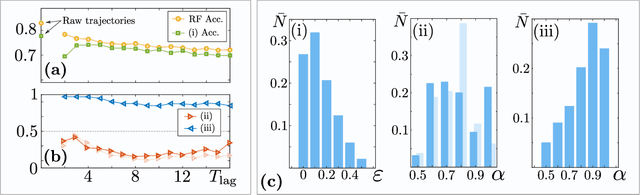
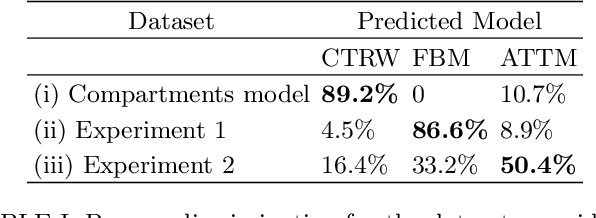
In order to study transport in complex environments, it is extremely important to determine the physical mechanism underlying diffusion, and precisely characterize its nature and parameters. Often, this task is strongly impacted by data consisting of trajectories with short length and limited localization precision. In this paper, we propose a machine learning method based on a random forest architecture, which is able to associate even very short trajectories to the underlying diffusion mechanism with a high accuracy. In addition, the method is able to classify the motion according to normal or anomalous diffusion, and determine its anomalous exponent with a small error. The method provides highly accurate outputs even when working with very short trajectories and in the presence of experimental noise. We further demonstrate the application of transfer learning to experimental and simulated data not included in the training/testing dataset. This allows for a full, high-accuracy characterization of experimental trajectories without the need of any prior information.