Learning minimal representations of stochastic processes with variational autoencoders

Stochastic processes have found numerous applications in science, as they are broadly used to model a variety of natural phenomena. Due to their intrinsic randomness and uncertainty, they are however difficult to characterize. Here, we introduce an unsupervised machine learning approach to determine the minimal set of parameters required to effectively describe the dynamics of a stochastic process. Our method builds upon an extended $\beta$-variational autoencoder architecture. By means of simulated datasets corresponding to paradigmatic diffusion models, we showcase its effectiveness in extracting the minimal relevant parameters that accurately describe these dynamics. Furthermore, the method enables the generation of new trajectories that faithfully replicate the expected stochastic behavior. Overall, our approach enables for the autonomous discovery of unknown parameters describing stochastic processes, hence enhancing our comprehension of complex phenomena across various fields.

Identifying Quantum Phase Transitions with Adversarial Neural Networks

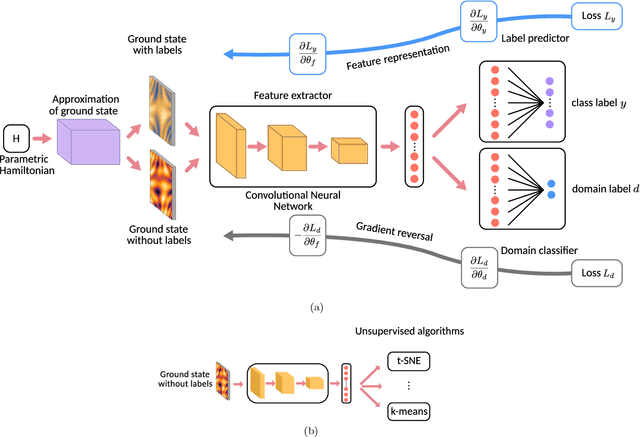
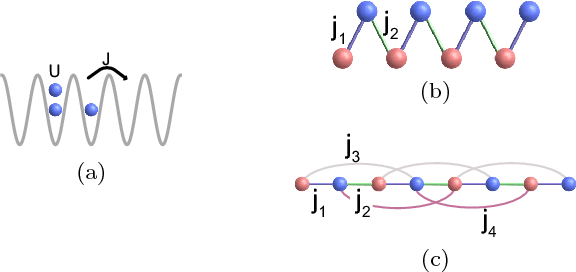
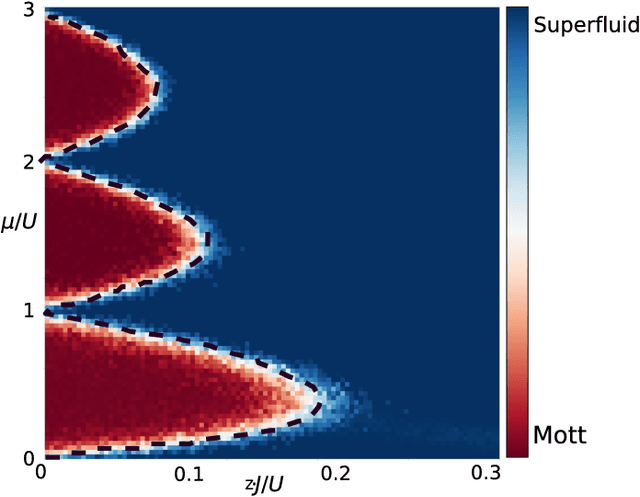
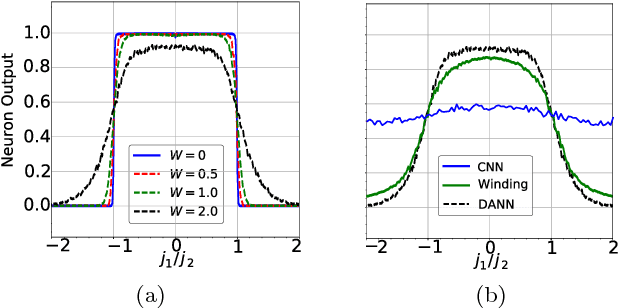
The identification of phases of matter is a challenging task, especially in quantum mechanics, where the complexity of the ground state appears to grow exponentially with the size of the system. We address this problem with state-of-the-art deep learning techniques: adversarial domain adaptation. We derive the phase diagram of the whole parameter space starting from a fixed and known subspace using unsupervised learning. The input data set contains both labeled and unlabeled data instances. The first kind is a system that admits an accurate analytical or numerical solution, and one can recover its phase diagram. The second type is the physical system with an unknown phase diagram. Adversarial domain adaptation uses both types of data to create invariant feature extracting layers in a deep learning architecture. Once these layers are trained, we can attach an unsupervised learner to the network to find phase transitions. We show the success of this technique by applying it on several paradigmatic models: the Ising model with different temperatures, the Bose-Hubbard model, and the SSH model with disorder. The input is the ground state without any manual feature engineering, and the dimension of the parameter space is unrestricted. The method finds unknown transitions successfully and predicts transition points in close agreement with standard methods. This study opens the door to the classification of physical systems where the phases boundaries are complex such as the many-body localization problem or the Bose glass phase.