Universal representation by Boltzmann machines with Regularised Axons

It is widely known that Boltzmann machines are capable of representing arbitrary probability distributions over the values of their visible neurons, given enough hidden ones. However, sampling -- and thus training -- these models can be numerically hard. Recently we proposed a regularisation of the connections of Boltzmann machines, in order to control the energy landscape of the model, paving a way for efficient sampling and training. Here we formally prove that such regularised Boltzmann machines preserve the ability to represent arbitrary distributions. This is in conjunction with controlling the number of energy local minima, thus enabling easy \emph{guided} sampling and training. Furthermore, we explicitly show that regularised Boltzmann machines can store exponentially many arbitrarily correlated visible patterns with perfect retrieval, and we connect them to the Dense Associative Memory networks.

Learning minimal representations of stochastic processes with variational autoencoders

Stochastic processes have found numerous applications in science, as they are broadly used to model a variety of natural phenomena. Due to their intrinsic randomness and uncertainty, they are however difficult to characterize. Here, we introduce an unsupervised machine learning approach to determine the minimal set of parameters required to effectively describe the dynamics of a stochastic process. Our method builds upon an extended $\beta$-variational autoencoder architecture. By means of simulated datasets corresponding to paradigmatic diffusion models, we showcase its effectiveness in extracting the minimal relevant parameters that accurately describe these dynamics. Furthermore, the method enables the generation of new trajectories that faithfully replicate the expected stochastic behavior. Overall, our approach enables for the autonomous discovery of unknown parameters describing stochastic processes, hence enhancing our comprehension of complex phenomena across various fields.

Preface: Characterisation of Physical Processes from Anomalous Diffusion Data

Preface to the special issue "Characterisation of Physical Processes from Anomalous Diffusion Data" associated with the Anomalous Diffusion Challenge ( https://andi-challenge.org ) and published in Journal of Physics A: Mathematical and Theoretical. The list of articles included in the special issue can be accessed at https://iopscience.iop.org/journal/1751-8121/page/Characterisation-of-Physical-Processes-from-Anomalous-Diffusion-Data .

Unsupervised learning of anomalous diffusion data

The characterization of diffusion processes is a keystone in our understanding of a variety of physical phenomena. Many of these deviate from Brownian motion, giving rise to anomalous diffusion. Various theoretical models exists nowadays to describe such processes, but their application to experimental setups is often challenging, due to the stochastic nature of the phenomena and the difficulty to harness reliable data. The latter often consists on short and noisy trajectories, which are hard to characterize with usual statistical approaches. In recent years, we have witnessed an impressive effort to bridge theory and experiments by means of supervised machine learning techniques, with astonishing results. In this work, we explore the use of unsupervised methods in anomalous diffusion data. We show that the main diffusion characteristics can be learnt without the need of any labelling of the data. We use such method to discriminate between anomalous diffusion models and extract their physical parameters. Moreover, we explore the feasibility of finding novel types of diffusion, in this case represented by compositions of existing diffusion models. At last, we showcase the use of the method in experimental data and demonstrate its advantages for cases where supervised learning is not applicable.

Efficient training of energy-based models via spin-glass control

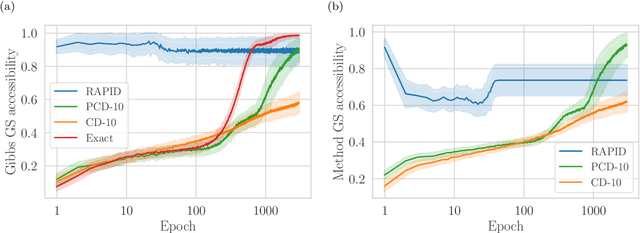
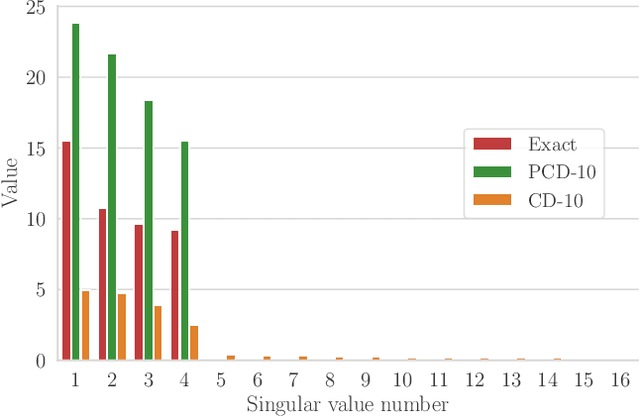
We present an efficient method for unsupervised learning using Boltzmann machines. The method is rooted in the control of the spin-glass properties of the Ising model described by the Boltzmann machine's weights. This allows for very easy access to low-energy configurations. We apply RAPID, the combination of Restricting the Axons (RA) of the model and training via Pattern-InDuced correlations (PID), to learn the Bars and Stripes dataset of various sizes and the MNIST dataset. We show how, in these tasks, RAPID quickly outperforms standard techniques for unsupervised learning in generalization ability. Indeed, both the number of epochs needed for effective learning and the computation time per training step are greatly reduced. In its simplest form, PID allows to compute the negative phase of the log-likelihood gradient with no Markov chain Monte Carlo sampling costs at all.

Quantum Compressed Sensing with Unsupervised Tensor Network Machine Learning

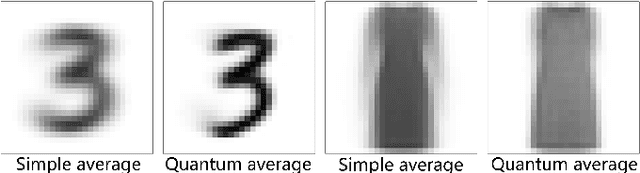
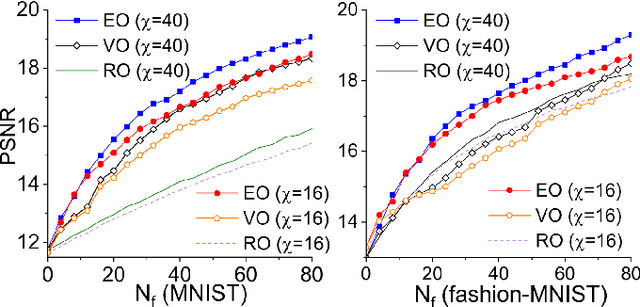
We propose tensor-network compressed sensing (TNCS) for compressing and communicating classical information via the quantum states trained by the unsupervised tensor network (TN) machine learning. The main task of TNCS is to reconstruct as accurately as possible the full classical information from a generative TN state, by knowing as small part of the classical information as possible. In the applications to the datasets of hand-written digits and fashion images, we train the generative TN (matrix product state) by the training set, and show that the images in the testing set can be reconstructed from a small number of pixels. Related issues including the applications of TNCS to quantum encrypted communication are discussed.

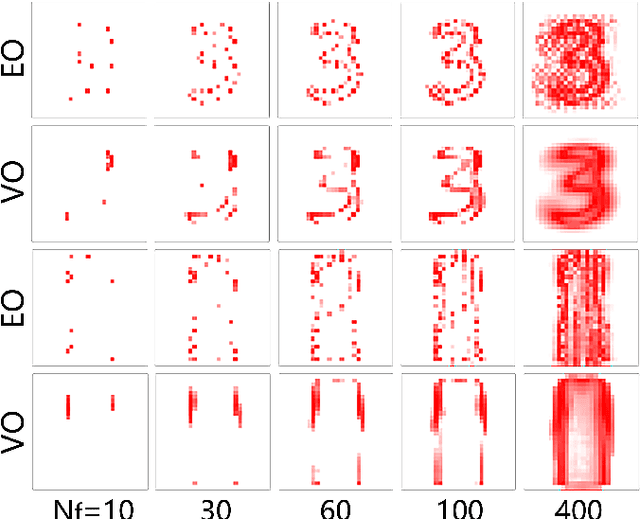
Machine learning method for single trajectory characterization

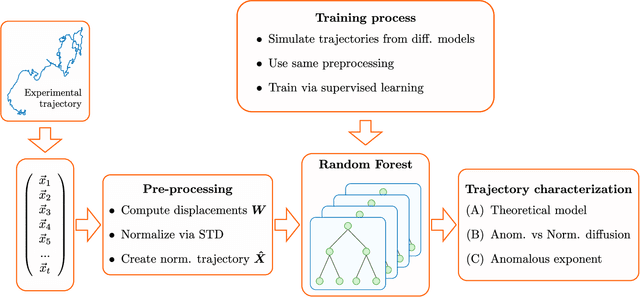
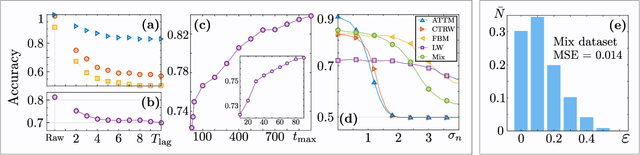
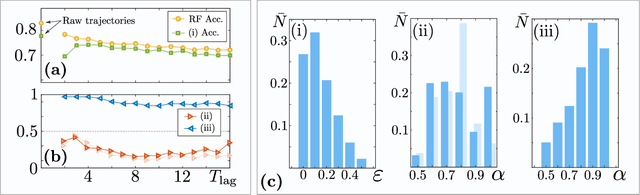
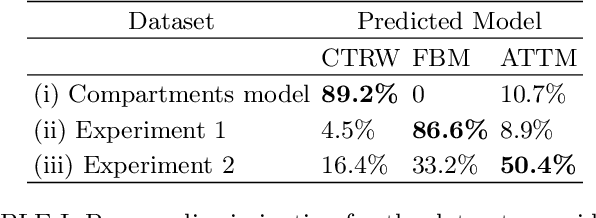
In order to study transport in complex environments, it is extremely important to determine the physical mechanism underlying diffusion, and precisely characterize its nature and parameters. Often, this task is strongly impacted by data consisting of trajectories with short length and limited localization precision. In this paper, we propose a machine learning method based on a random forest architecture, which is able to associate even very short trajectories to the underlying diffusion mechanism with a high accuracy. In addition, the method is able to classify the motion according to normal or anomalous diffusion, and determine its anomalous exponent with a small error. The method provides highly accurate outputs even when working with very short trajectories and in the presence of experimental noise. We further demonstrate the application of transfer learning to experimental and simulated data not included in the training/testing dataset. This allows for a full, high-accuracy characterization of experimental trajectories without the need of any prior information.

Machine Learning by Two-Dimensional Hierarchical Tensor Networks: A Quantum Information Theoretic Perspective on Deep Architectures

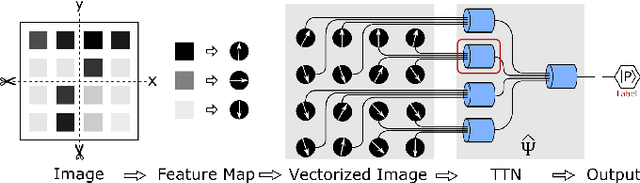
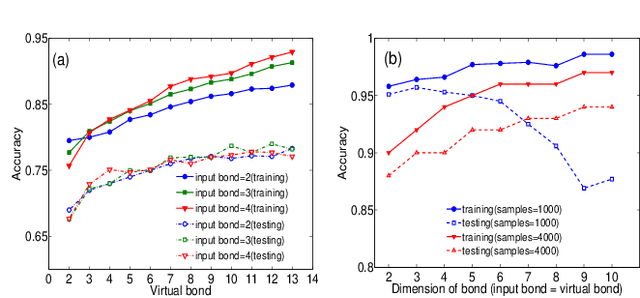
The resemblance between the methods used in quantum-many body physics and in machine learning has drawn considerable attention. In particular, tensor networks (TNs) and deep learning architectures bear striking similarities to the extent that TNs can be used for machine learning. Previous results used one-dimensional TNs in image recognition, showing limited scalability and flexibilities. In this work, we train two-dimensional hierarchical TNs to solve image recognition problems, using a training algorithm derived from the multipartite entanglement renormalization ansatz. This approach introduces novel mathematical connections among quantum many-body physics, quantum information theory, and machine learning. While keeping the TN unitary in the training phase, TN states are defined, which optimally encode classes of images into quantum many-body states. We study the quantum features of the TN states, including quantum entanglement and fidelity. We find these quantities could be novel properties that characterize the image classes, as well as the machine learning tasks. Our work could contribute to the research on identifying/modeling quantum artificial intelligences.

Entanglement-guided architectures of machine learning by quantum tensor network

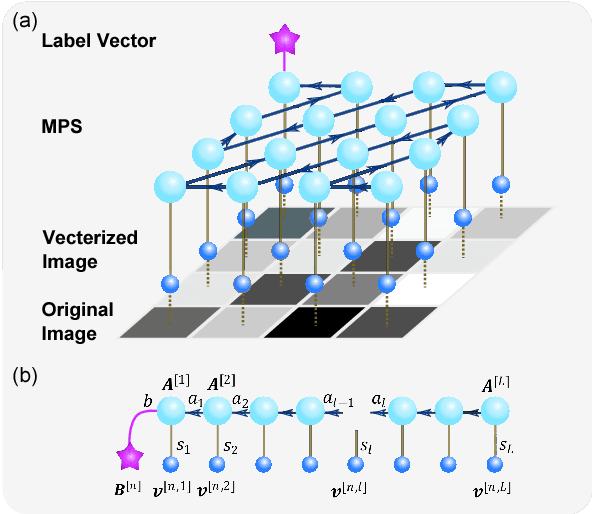
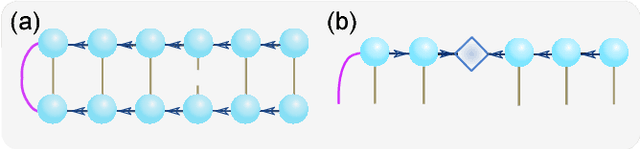
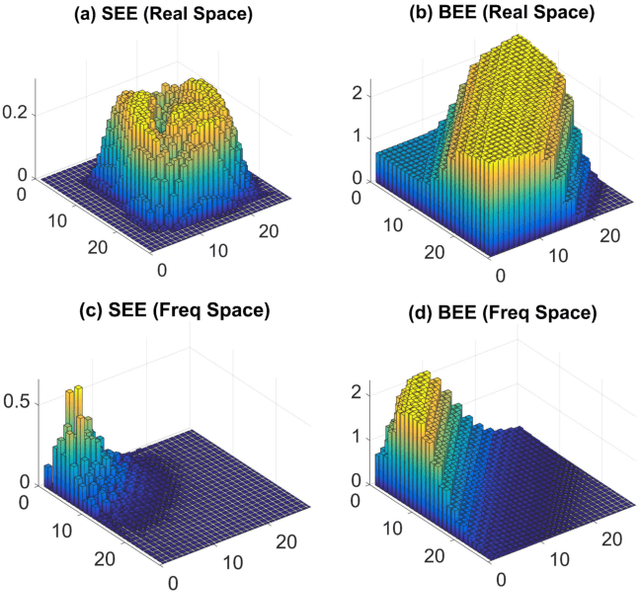
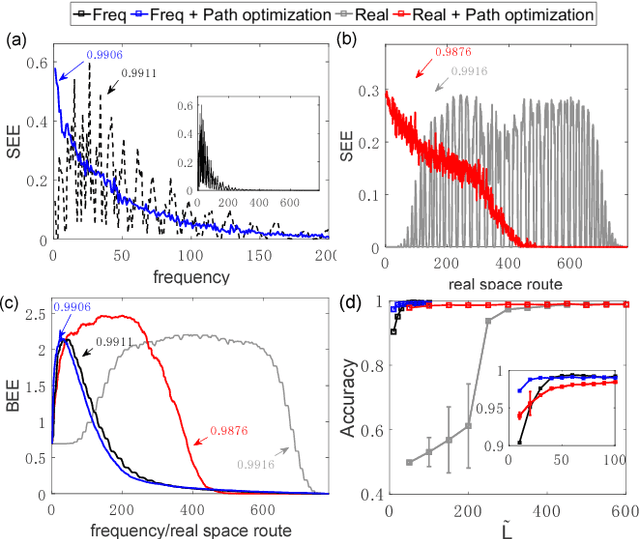
It is a fundamental, but still elusive question whether the schemes based on quantum mechanics, in particular on quantum entanglement, can be used for classical information processing and machine learning. Even partial answer to this question would bring important insights to both fields of machine learning and quantum mechanics. In this work, we implement simple numerical experiments, related to pattern/images classification, in which we represent the classifiers by many-qubit quantum states written in the matrix product states (MPS). Classical machine learning algorithm is applied to these quantum states to learn the classical data. We explicitly show how quantum entanglement (i.e., single-site and bipartite entanglement) can emerge in such represented images. Entanglement characterizes here the importance of data, and such information are practically used to guide the architecture of MPS, and improve the efficiency. The number of needed qubits can be reduced to less than 1/10 of the original number, which is within the access of the state-of-the-art quantum computers. We expect such numerical experiments could open new paths in charactering classical machine learning algorithms, and at the same time shed lights on the generic quantum simulations/computations of machine learning tasks.