Machine Learning by Two-Dimensional Hierarchical Tensor Networks: A Quantum Information Theoretic Perspective on Deep Architectures

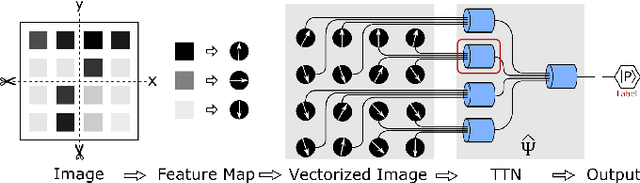
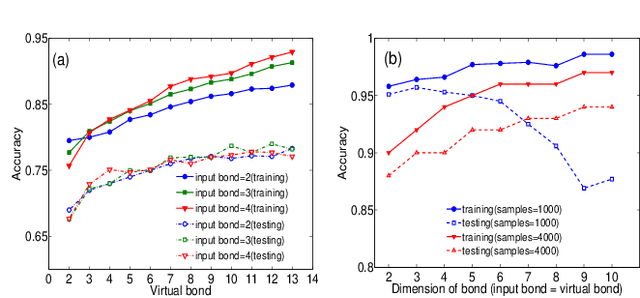
The resemblance between the methods used in quantum-many body physics and in machine learning has drawn considerable attention. In particular, tensor networks (TNs) and deep learning architectures bear striking similarities to the extent that TNs can be used for machine learning. Previous results used one-dimensional TNs in image recognition, showing limited scalability and flexibilities. In this work, we train two-dimensional hierarchical TNs to solve image recognition problems, using a training algorithm derived from the multipartite entanglement renormalization ansatz. This approach introduces novel mathematical connections among quantum many-body physics, quantum information theory, and machine learning. While keeping the TN unitary in the training phase, TN states are defined, which optimally encode classes of images into quantum many-body states. We study the quantum features of the TN states, including quantum entanglement and fidelity. We find these quantities could be novel properties that characterize the image classes, as well as the machine learning tasks. Our work could contribute to the research on identifying/modeling quantum artificial intelligences.