Transformer-based Drum-level Prediction in a Boiler Plant with Delayed Relations among Multivariates

The steam drum water level is a critical parameter that directly impacts the safety and efficiency of power plant operations. However, predicting the drum water level in boilers is challenging due to complex non-linear process dynamics originating from long-time delays and interrelations, as well as measurement noise. This paper investigates the application of Transformer-based models for predicting drum water levels in a steam boiler plant. Leveraging the capabilities of Transformer architectures, this study aims to develop an accurate and robust predictive framework to anticipate water level fluctuations and facilitate proactive control strategies. To this end, a prudent pipeline is proposed, including 1) data preprocess, 2) causal relation analysis, 3) delay inference, 4) variable augmentation, and 5) prediction. Through extensive experimentation and analysis, the effectiveness of Transformer-based approaches in steam drum water level prediction is evaluated, highlighting their potential to enhance operational stability and optimize plant performance.

Tensor networks for interpretable and efficient quantum-inspired machine learning

It is a critical challenge to simultaneously gain high interpretability and efficiency with the current schemes of deep machine learning (ML). Tensor network (TN), which is a well-established mathematical tool originating from quantum mechanics, has shown its unique advantages on developing efficient ``white-box'' ML schemes. Here, we give a brief review on the inspiring progresses made in TN-based ML. On one hand, interpretability of TN ML is accommodated with the solid theoretical foundation based on quantum information and many-body physics. On the other hand, high efficiency can be rendered from the powerful TN representations and the advanced computational techniques developed in quantum many-body physics. With the fast development on quantum computers, TN is expected to conceive novel schemes runnable on quantum hardware, heading towards the ``quantum artificial intelligence'' in the forthcoming future.

Intelligent diagnostic scheme for lung cancer screening with Raman spectra data by tensor network machine learning

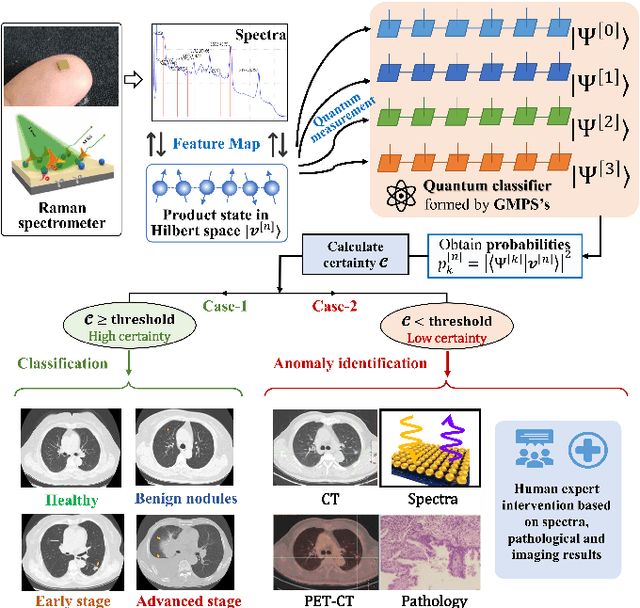
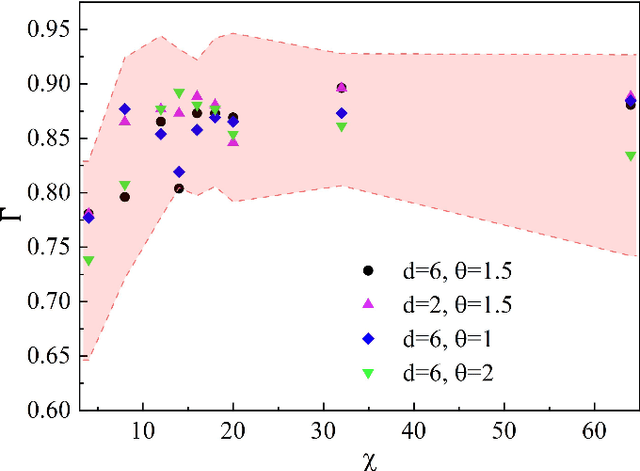
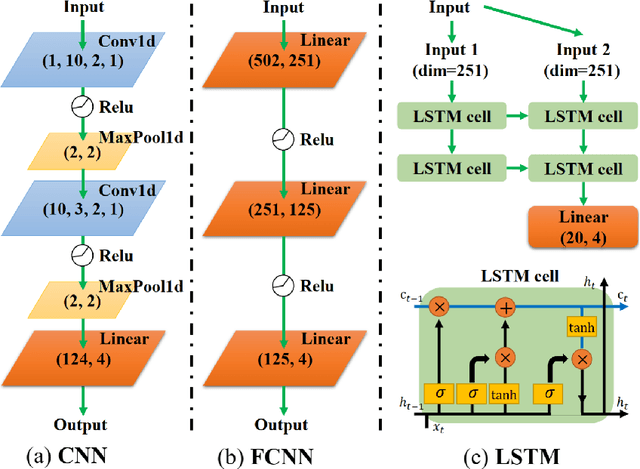
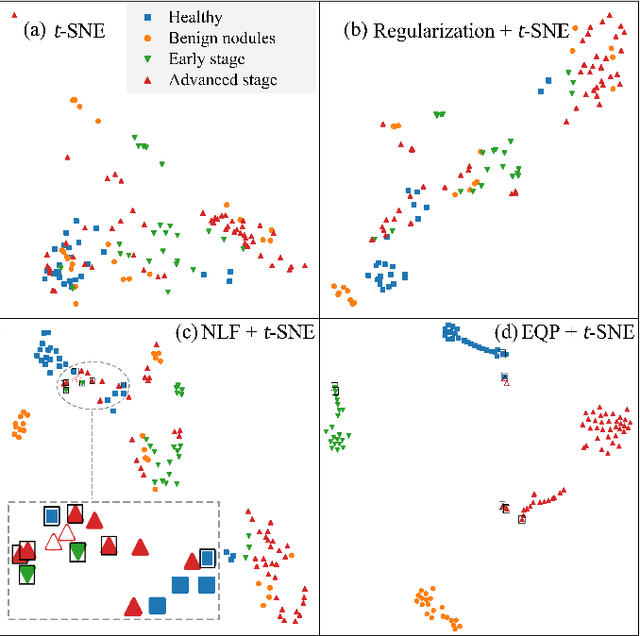
Artificial intelligence (AI) has brought tremendous impacts on biomedical sciences from academic researches to clinical applications, such as in biomarkers' detection and diagnosis, optimization of treatment, and identification of new therapeutic targets in drug discovery. However, the contemporary AI technologies, particularly deep machine learning (ML), severely suffer from non-interpretability, which might uncontrollably lead to incorrect predictions. Interpretability is particularly crucial to ML for clinical diagnosis as the consumers must gain necessary sense of security and trust from firm grounds or convincing interpretations. In this work, we propose a tensor-network (TN)-ML method to reliably predict lung cancer patients and their stages via screening Raman spectra data of Volatile organic compounds (VOCs) in exhaled breath, which are generally suitable as biomarkers and are considered to be an ideal way for non-invasive lung cancer screening. The prediction of TN-ML is based on the mutual distances of the breath samples mapped to the quantum Hilbert space. Thanks to the quantum probabilistic interpretation, the certainty of the predictions can be quantitatively characterized. The accuracy of the samples with high certainty is almost 100$\%$. The incorrectly-classified samples exhibit obviously lower certainty, and thus can be decipherably identified as anomalies, which will be handled by human experts to guarantee high reliability. Our work sheds light on shifting the ``AI for biomedical sciences'' from the conventional non-interpretable ML schemes to the interpretable human-ML interactive approaches, for the purpose of high accuracy and reliability.

Tangent-Space Gradient Optimization of Tensor Network for Machine Learning

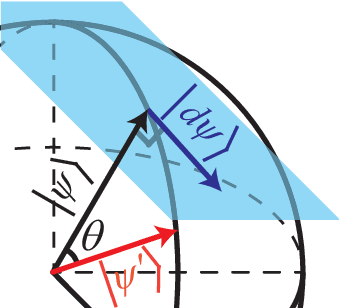
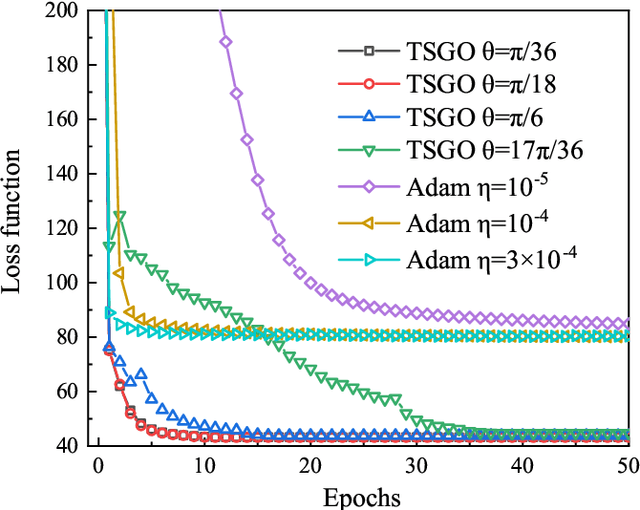
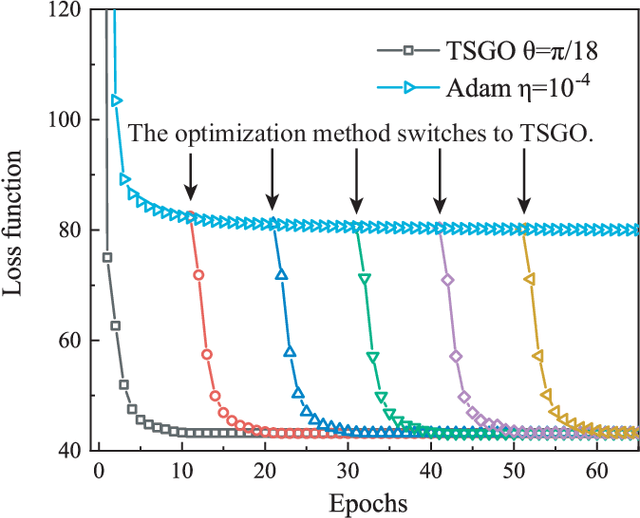
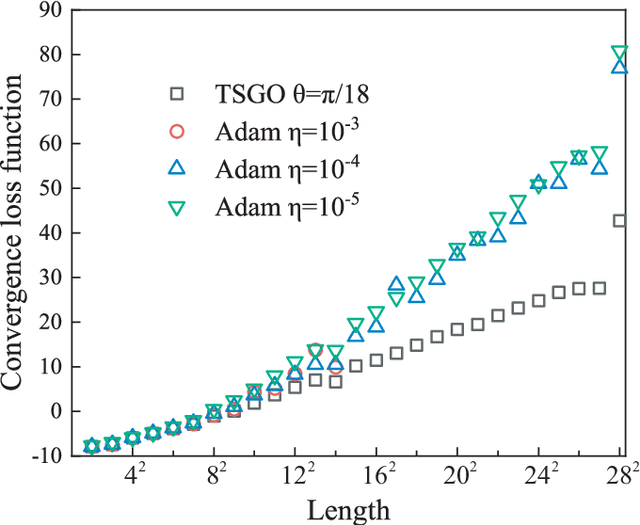
The gradient-based optimization method for deep machine learning models suffers from gradient vanishing and exploding problems, particularly when the computational graph becomes deep. In this work, we propose the tangent-space gradient optimization (TSGO) for the probabilistic models to keep the gradients from vanishing or exploding. The central idea is to guarantee the orthogonality between the variational parameters and the gradients. The optimization is then implemented by rotating parameter vector towards the direction of gradient. We explain and testify TSGO in tensor network (TN) machine learning, where the TN describes the joint probability distribution as a normalized state $\left| \psi \right\rangle $ in Hilbert space. We show that the gradient can be restricted in the tangent space of $\left\langle \psi \right.\left| \psi \right\rangle = 1$ hyper-sphere. Instead of additional adaptive methods to control the learning rate in deep learning, the learning rate of TSGO is naturally determined by the angle $\theta $ as $\eta = \tan \theta $. Our numerical results reveal better convergence of TSGO in comparison to the off-the-shelf Adam.

Quantum Compressed Sensing with Unsupervised Tensor Network Machine Learning

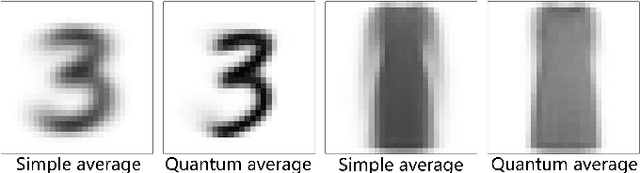
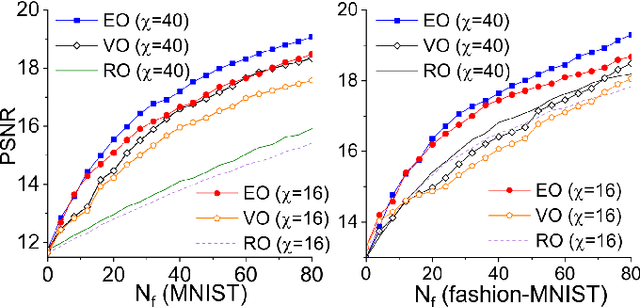
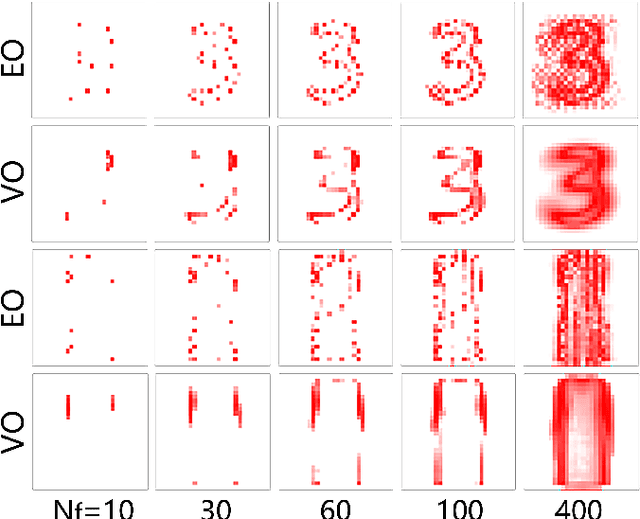
We propose tensor-network compressed sensing (TNCS) for compressing and communicating classical information via the quantum states trained by the unsupervised tensor network (TN) machine learning. The main task of TNCS is to reconstruct as accurately as possible the full classical information from a generative TN state, by knowing as small part of the classical information as possible. In the applications to the datasets of hand-written digits and fashion images, we train the generative TN (matrix product state) by the training set, and show that the images in the testing set can be reconstructed from a small number of pixels. Related issues including the applications of TNCS to quantum encrypted communication are discussed.

Generative Tensor Network Classification Model for Supervised Machine Learning

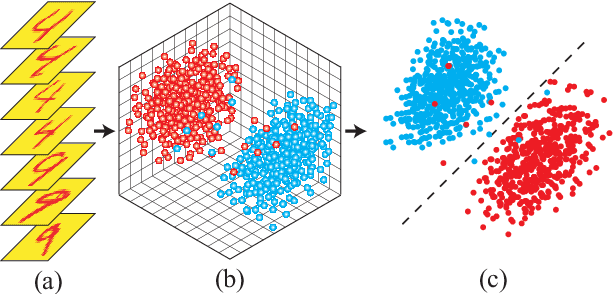
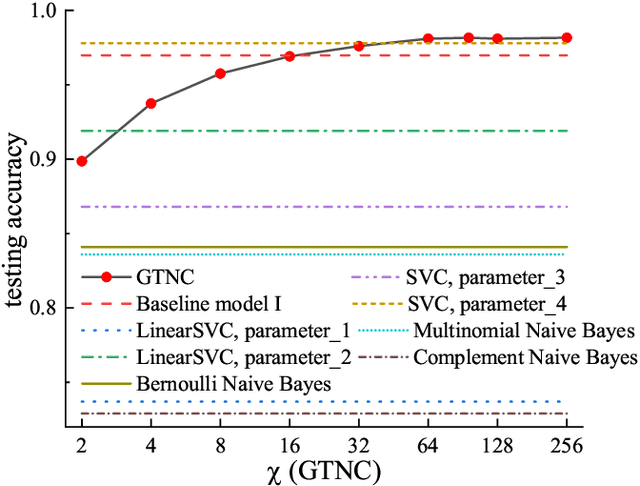
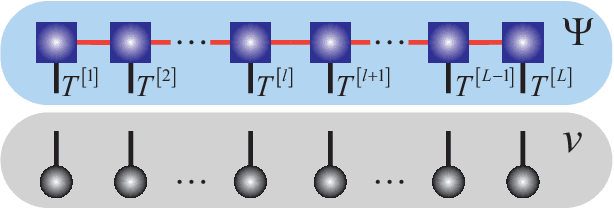
Tensor network (TN) has recently triggered extensive interests in developing machine-learning models in quantum many-body Hilbert space. Here we purpose a generative TN classification (GTNC) approach for supervised learning. The strategy is to train the generative TN for each class of the samples to construct the classifiers. The classification is implemented by comparing the distance in the many-body Hilbert space. The numerical experiments by GTNC show impressive performance on the MNIST and Fashion-MNIST dataset. The testing accuracy is competitive to the state-of-the-art convolutional neural network while higher than the naive Bayes classifier (a generative classifier) and support vector machine. Moreover, GTNC is more efficient than the existing TN models that are in general discriminative. By investigating the distances in the many-body Hilbert space, we find that (a) the samples are naturally clustering in such a space; and (b) bounding the bond dimensions of the TN's to finite values corresponds to removing redundant information in the image recognition. These two characters make GTNC an adaptive and universal model of excellent performance.

Machine Learning by Two-Dimensional Hierarchical Tensor Networks: A Quantum Information Theoretic Perspective on Deep Architectures

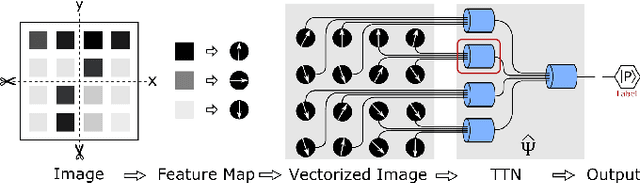
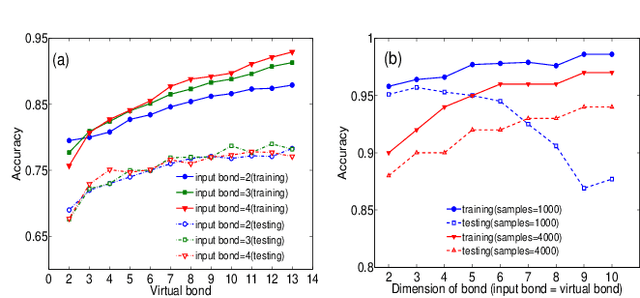
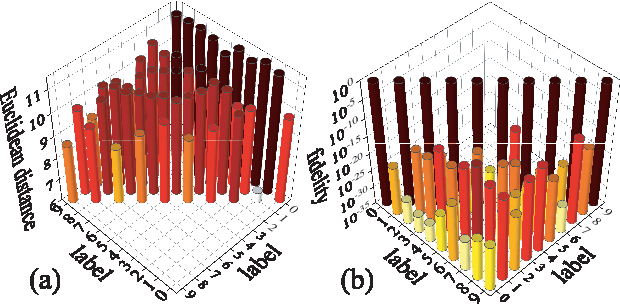
The resemblance between the methods used in quantum-many body physics and in machine learning has drawn considerable attention. In particular, tensor networks (TNs) and deep learning architectures bear striking similarities to the extent that TNs can be used for machine learning. Previous results used one-dimensional TNs in image recognition, showing limited scalability and flexibilities. In this work, we train two-dimensional hierarchical TNs to solve image recognition problems, using a training algorithm derived from the multipartite entanglement renormalization ansatz. This approach introduces novel mathematical connections among quantum many-body physics, quantum information theory, and machine learning. While keeping the TN unitary in the training phase, TN states are defined, which optimally encode classes of images into quantum many-body states. We study the quantum features of the TN states, including quantum entanglement and fidelity. We find these quantities could be novel properties that characterize the image classes, as well as the machine learning tasks. Our work could contribute to the research on identifying/modeling quantum artificial intelligences.