Universal scaling laws in quantum-probabilistic machine learning by tensor network towards interpreting representation and generalization powers

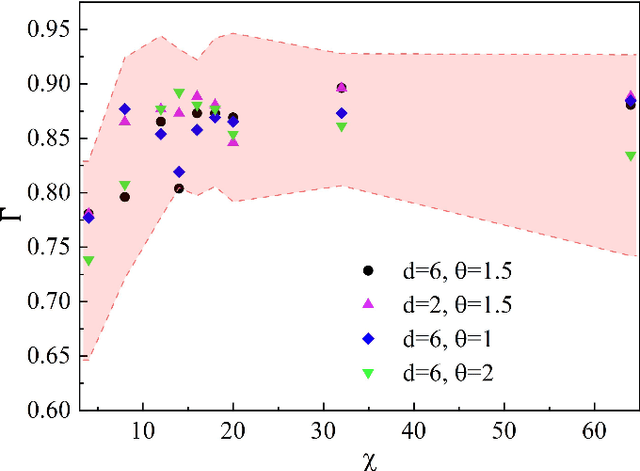
Interpreting the representation and generalization powers has been a long-standing issue in the field of machine learning (ML) and artificial intelligence. This work contributes to uncovering the emergence of universal scaling laws in quantum-probabilistic ML. We take the generative tensor network (GTN) in the form of a matrix product state as an example and show that with an untrained GTN (such as a random TN state), the negative logarithmic likelihood (NLL) $L$ generally increases linearly with the number of features $M$, i.e., $L \simeq k M + const$. This is a consequence of the so-called ``catastrophe of orthogonality,'' which states that quantum many-body states tend to become exponentially orthogonal to each other as $M$ increases. We reveal that while gaining information through training, the linear scaling law is suppressed by a negative quadratic correction, leading to $L \simeq \beta M - \alpha M^2 + const$. The scaling coefficients exhibit logarithmic relationships with the number of training samples and the number of quantum channels $\chi$. The emergence of the quadratic correction term in NLL for the testing (training) set can be regarded as evidence of the generalization (representation) power of GTN. Over-parameterization can be identified by the deviation in the values of $\alpha$ between training and testing sets while increasing $\chi$. We further investigate how orthogonality in the quantum feature map relates to the satisfaction of quantum probabilistic interpretation, as well as to the representation and generalization powers of GTN. The unveiling of universal scaling laws in quantum-probabilistic ML would be a valuable step toward establishing a white-box ML scheme interpreted within the quantum probabilistic framework.

Universal replication of chaotic characteristics by classical and quantum machine learning

Replicating chaotic characteristics of non-linear dynamics by machine learning (ML) has recently drawn wide attentions. In this work, we propose that a ML model, trained to predict the state one-step-ahead from several latest historic states, can accurately replicate the bifurcation diagram and the Lyapunov exponents of discrete dynamic systems. The characteristics for different values of the hyper-parameters are captured universally by a single ML model, while the previous works considered training the ML model independently by fixing the hyper-parameters to be specific values. Our benchmarks on the one- and two-dimensional Logistic maps show that variational quantum circuit can reproduce the long-term characteristics with higher accuracy than the long short-term memory (a well-recognized classical ML model). Our work reveals an essential difference between the ML for the chaotic characteristics and that for standard tasks, from the perspective of the relation between performance and model complexity. Our results suggest that quantum circuit model exhibits potential advantages on mitigating over-fitting, achieving higher accuracy and stability.

Intelligent diagnostic scheme for lung cancer screening with Raman spectra data by tensor network machine learning

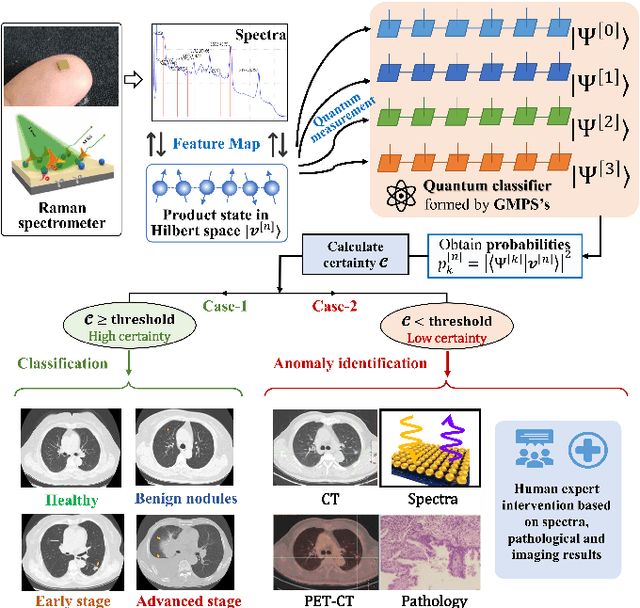
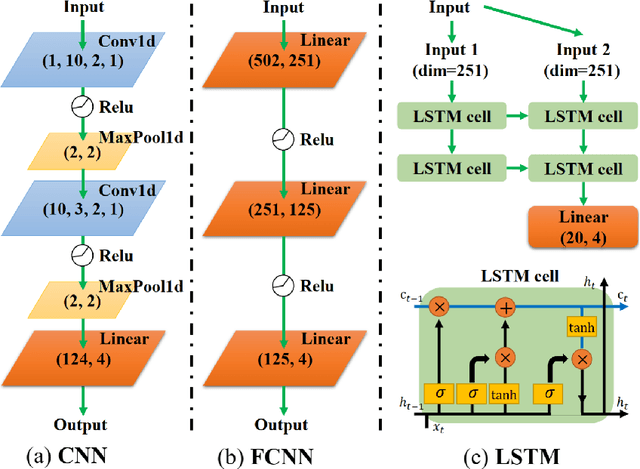
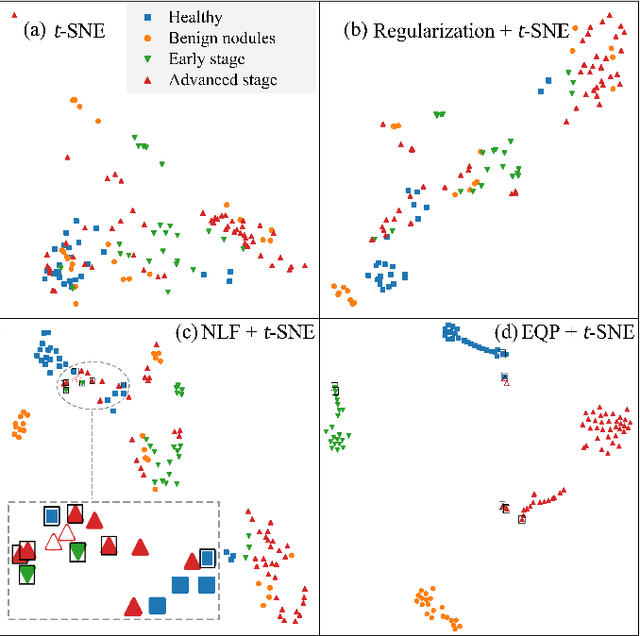
Artificial intelligence (AI) has brought tremendous impacts on biomedical sciences from academic researches to clinical applications, such as in biomarkers' detection and diagnosis, optimization of treatment, and identification of new therapeutic targets in drug discovery. However, the contemporary AI technologies, particularly deep machine learning (ML), severely suffer from non-interpretability, which might uncontrollably lead to incorrect predictions. Interpretability is particularly crucial to ML for clinical diagnosis as the consumers must gain necessary sense of security and trust from firm grounds or convincing interpretations. In this work, we propose a tensor-network (TN)-ML method to reliably predict lung cancer patients and their stages via screening Raman spectra data of Volatile organic compounds (VOCs) in exhaled breath, which are generally suitable as biomarkers and are considered to be an ideal way for non-invasive lung cancer screening. The prediction of TN-ML is based on the mutual distances of the breath samples mapped to the quantum Hilbert space. Thanks to the quantum probabilistic interpretation, the certainty of the predictions can be quantitatively characterized. The accuracy of the samples with high certainty is almost 100$\%$. The incorrectly-classified samples exhibit obviously lower certainty, and thus can be decipherably identified as anomalies, which will be handled by human experts to guarantee high reliability. Our work sheds light on shifting the ``AI for biomedical sciences'' from the conventional non-interpretable ML schemes to the interpretable human-ML interactive approaches, for the purpose of high accuracy and reliability.

Unsupervised Recognition of Informative Features via Tensor Network Machine Learning and Quantum Entanglement Variations

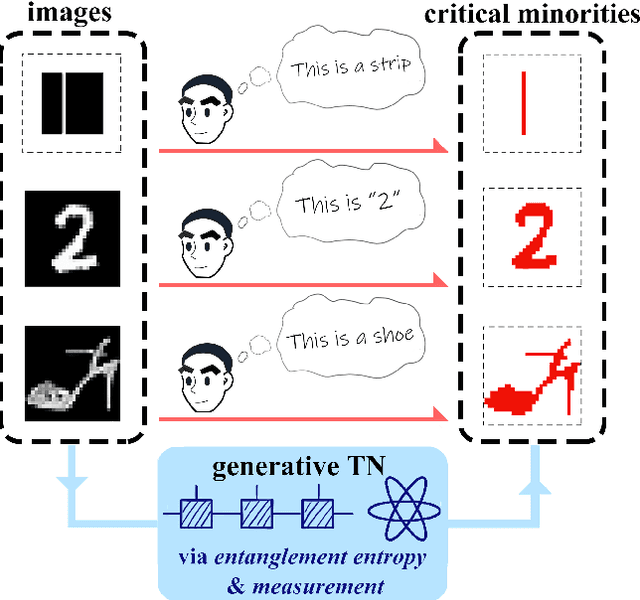
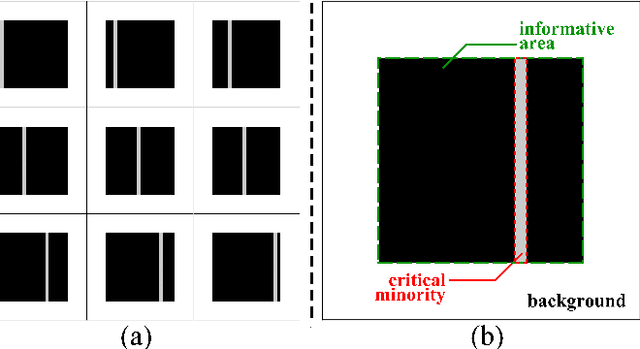
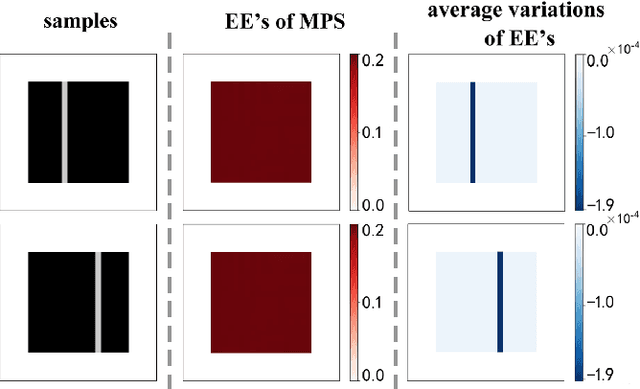
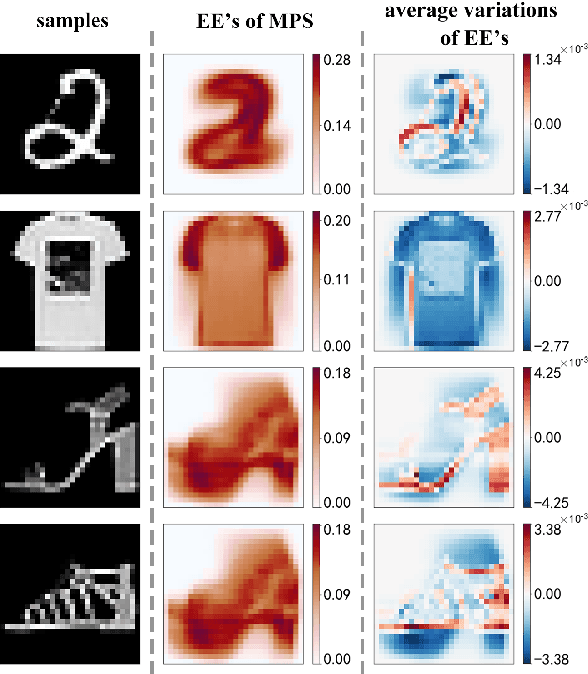
Given an image of a white shoe drawn on a blackboard, how are the white pixels deemed (say by human minds) to be informative for recognizing the shoe without any labeling information on the pixels? Here we investigate such a "white shoe" recognition problem from the perspective of tensor network (TN) machine learning and quantum entanglement. Utilizing a generative TN that captures the probability distribution of the features as quantum amplitudes, we propose an unsupervised recognition scheme of informative features with the variations of entanglement entropy (EE) caused by designed measurements. In this way, a given sample, where the values of its features are statistically meaningless, is mapped to the variations of EE that are statistically meaningful. We show that the EE variations identify the features that are critical to recognize this specific sample, and the EE itself reveals the information distribution from the TN model. The signs of the variations further reveal the entanglement structures among the features. We test the validity of our scheme on a toy dataset of strip images, the MNIST dataset of hand-drawn digits, and the fashion-MNIST dataset of the pictures of fashion articles. Our scheme opens the avenue to the quantum-inspired and interpreted unsupervised learning and could be applied to, e.g., image segmentation and object detection.