Universal scaling laws in quantum-probabilistic machine learning by tensor network towards interpreting representation and generalization powers

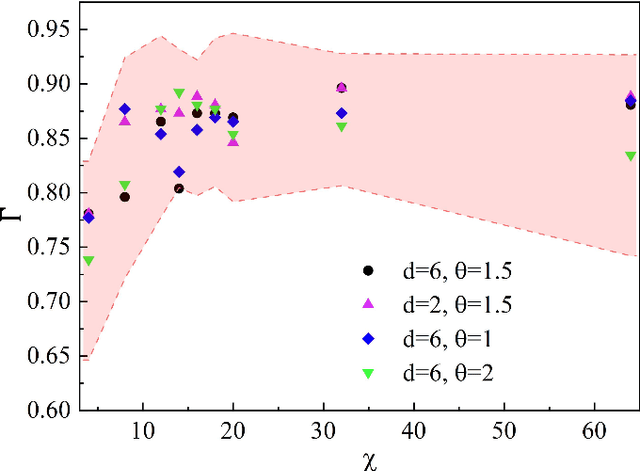
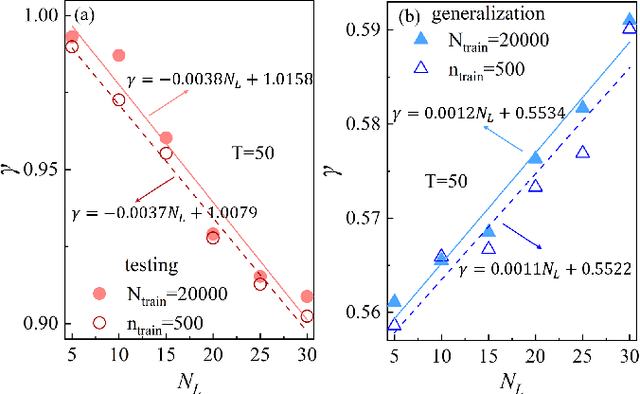
Interpreting the representation and generalization powers has been a long-standing issue in the field of machine learning (ML) and artificial intelligence. This work contributes to uncovering the emergence of universal scaling laws in quantum-probabilistic ML. We take the generative tensor network (GTN) in the form of a matrix product state as an example and show that with an untrained GTN (such as a random TN state), the negative logarithmic likelihood (NLL) $L$ generally increases linearly with the number of features $M$, i.e., $L \simeq k M + const$. This is a consequence of the so-called ``catastrophe of orthogonality,'' which states that quantum many-body states tend to become exponentially orthogonal to each other as $M$ increases. We reveal that while gaining information through training, the linear scaling law is suppressed by a negative quadratic correction, leading to $L \simeq \beta M - \alpha M^2 + const$. The scaling coefficients exhibit logarithmic relationships with the number of training samples and the number of quantum channels $\chi$. The emergence of the quadratic correction term in NLL for the testing (training) set can be regarded as evidence of the generalization (representation) power of GTN. Over-parameterization can be identified by the deviation in the values of $\alpha$ between training and testing sets while increasing $\chi$. We further investigate how orthogonality in the quantum feature map relates to the satisfaction of quantum probabilistic interpretation, as well as to the representation and generalization powers of GTN. The unveiling of universal scaling laws in quantum-probabilistic ML would be a valuable step toward establishing a white-box ML scheme interpreted within the quantum probabilistic framework.

Universal replication of chaotic characteristics by classical and quantum machine learning

Replicating chaotic characteristics of non-linear dynamics by machine learning (ML) has recently drawn wide attentions. In this work, we propose that a ML model, trained to predict the state one-step-ahead from several latest historic states, can accurately replicate the bifurcation diagram and the Lyapunov exponents of discrete dynamic systems. The characteristics for different values of the hyper-parameters are captured universally by a single ML model, while the previous works considered training the ML model independently by fixing the hyper-parameters to be specific values. Our benchmarks on the one- and two-dimensional Logistic maps show that variational quantum circuit can reproduce the long-term characteristics with higher accuracy than the long short-term memory (a well-recognized classical ML model). Our work reveals an essential difference between the ML for the chaotic characteristics and that for standard tasks, from the perspective of the relation between performance and model complexity. Our results suggest that quantum circuit model exhibits potential advantages on mitigating over-fitting, achieving higher accuracy and stability.

Tensor networks for interpretable and efficient quantum-inspired machine learning

It is a critical challenge to simultaneously gain high interpretability and efficiency with the current schemes of deep machine learning (ML). Tensor network (TN), which is a well-established mathematical tool originating from quantum mechanics, has shown its unique advantages on developing efficient ``white-box'' ML schemes. Here, we give a brief review on the inspiring progresses made in TN-based ML. On one hand, interpretability of TN ML is accommodated with the solid theoretical foundation based on quantum information and many-body physics. On the other hand, high efficiency can be rendered from the powerful TN representations and the advanced computational techniques developed in quantum many-body physics. With the fast development on quantum computers, TN is expected to conceive novel schemes runnable on quantum hardware, heading towards the ``quantum artificial intelligence'' in the forthcoming future.

Persistent Ballistic Entanglement Spreading with Optimal Control in Quantum Spin Chains

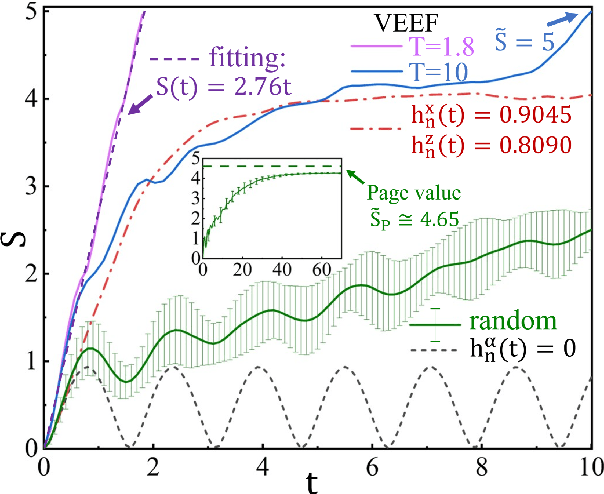
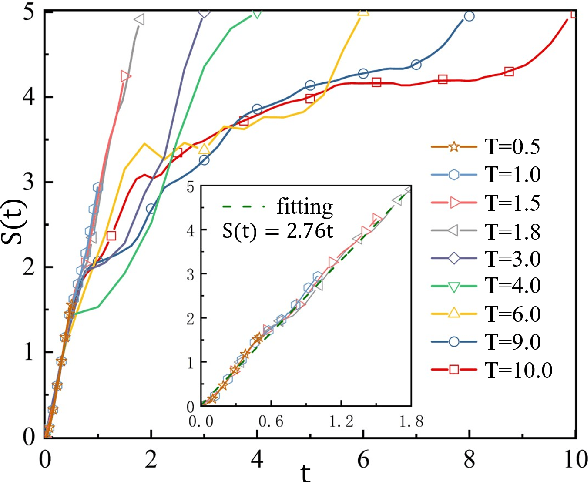
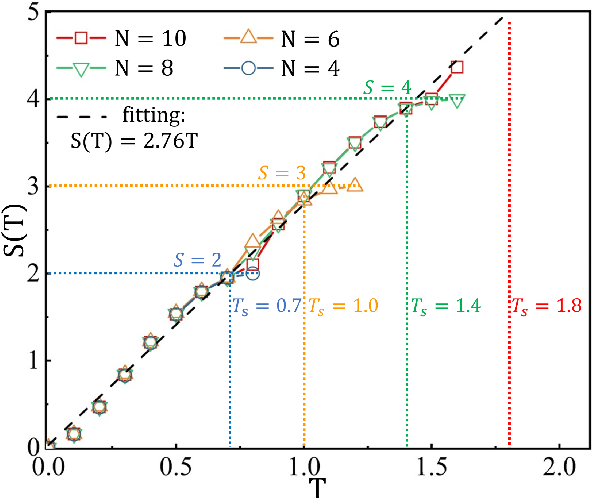
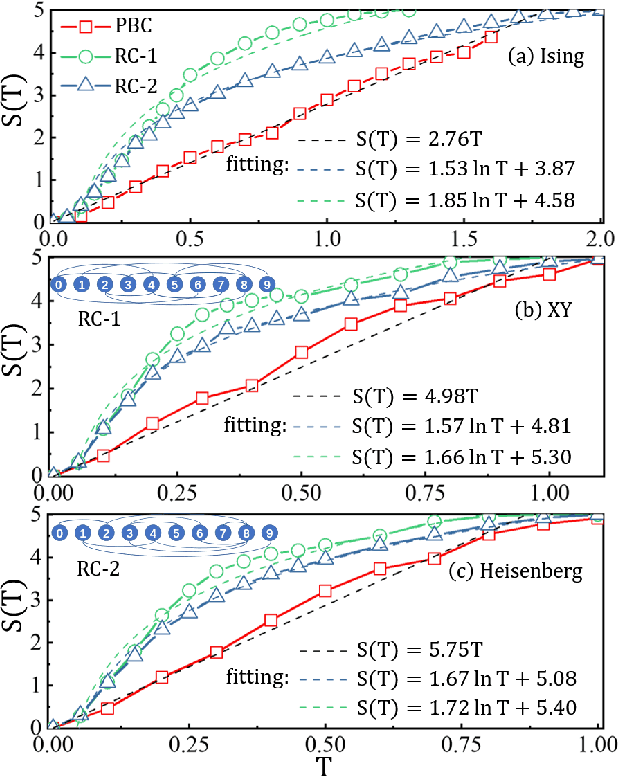
Entanglement propagation provides a key routine to understand quantum many-body dynamics in and out of equilibrium. In this work, we uncover that the ``variational entanglement-enhancing'' field (VEEF) robustly induces a persistent ballistic spreading of entanglement in quantum spin chains. The VEEF is time dependent, and is optimally controlled to maximize the bipartite entanglement entropy (EE) of the final state. Such a linear growth persists till the EE reaches the genuine saturation $\tilde{S} = - \log_{2} 2^{-\frac{N}{2}}=\frac{N}{2}$ with $N$ the total number of spins. The EE satisfies $S(t) = v t$ for the time $t \leq \frac{N}{2v}$, with $v$ the velocity. These results are in sharp contrast with the behaviors without VEEF, where the EE generally approaches a sub-saturation known as the Page value $\tilde{S}_{P} =\tilde{S} - \frac{1}{2\ln{2}}$ in the long-time limit, and the entanglement growth deviates from being linear before the Page value is reached. The dependence between the velocity and interactions is explored, with $v \simeq 2.76$, $4.98$, and $5.75$ for the spin chains with Ising, XY, and Heisenberg interactions, respectively. We further show that the nonlinear growth of EE emerges with the presence of long-range interactions.

Compressing neural network by tensor network with exponentially fewer variational parameters

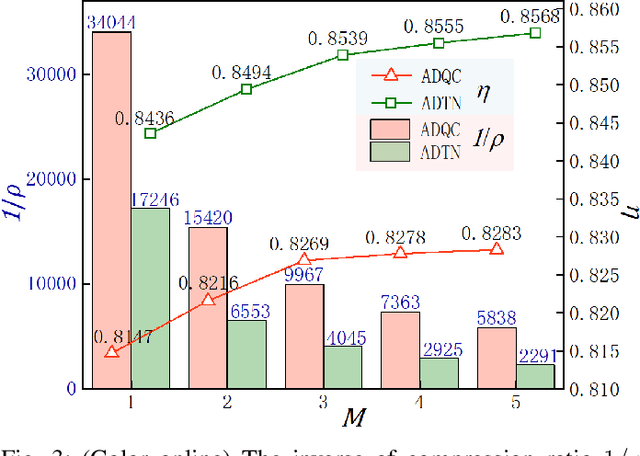
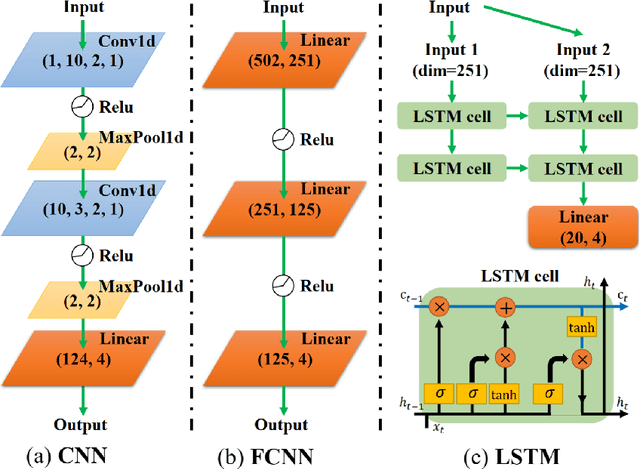
Neural network (NN) designed for challenging machine learning tasks is in general a highly nonlinear mapping that contains massive variational parameters. High complexity of NN, if unbounded or unconstrained, might unpredictably cause severe issues including over-fitting, loss of generalization power, and unbearable cost of hardware. In this work, we propose a general compression scheme that significantly reduces the variational parameters of NN by encoding them to multi-layer tensor networks (TN's) that contain exponentially-fewer free parameters. Superior compression performance of our scheme is demonstrated on several widely-recognized NN's (FC-2, LeNet-5, and VGG-16) and datasets (MNIST and CIFAR-10), surpassing the state-of-the-art method based on shallow tensor networks. For instance, about 10 million parameters in the three convolutional layers of VGG-16 are compressed in TN's with just $632$ parameters, while the testing accuracy on CIFAR-10 is surprisingly improved from $81.14\%$ by the original NN to $84.36\%$ after compression. Our work suggests TN as an exceptionally efficient mathematical structure for representing the variational parameters of NN's, which superiorly exploits the compressibility than the simple multi-way arrays.

Intelligent diagnostic scheme for lung cancer screening with Raman spectra data by tensor network machine learning

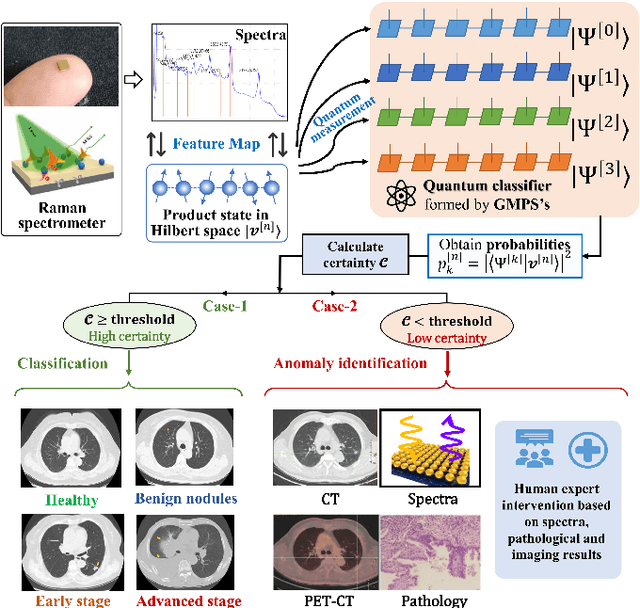
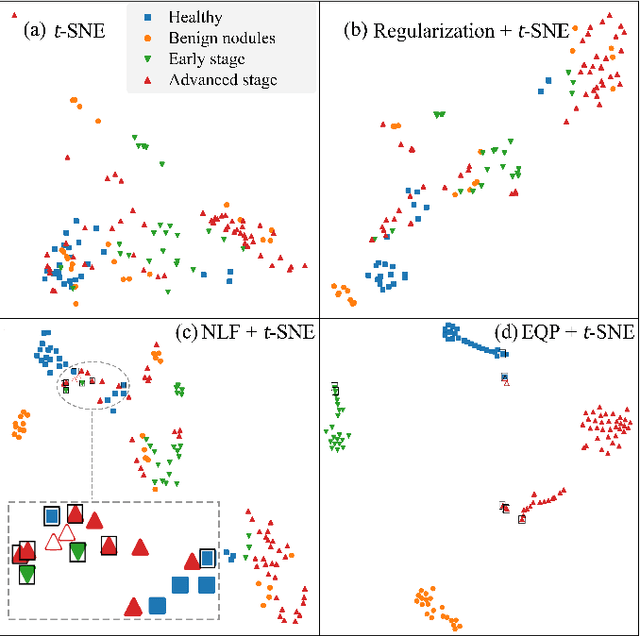
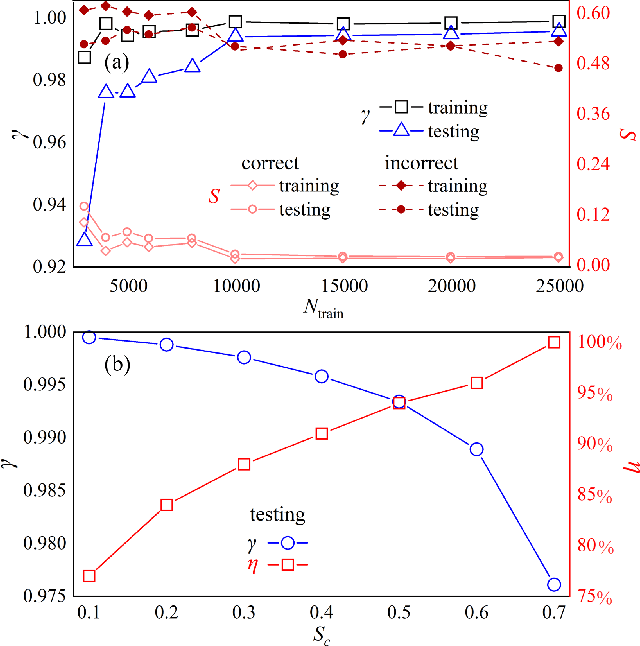
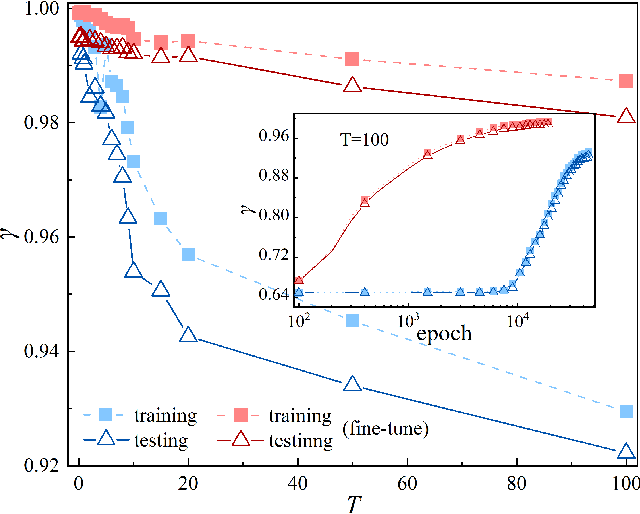
Artificial intelligence (AI) has brought tremendous impacts on biomedical sciences from academic researches to clinical applications, such as in biomarkers' detection and diagnosis, optimization of treatment, and identification of new therapeutic targets in drug discovery. However, the contemporary AI technologies, particularly deep machine learning (ML), severely suffer from non-interpretability, which might uncontrollably lead to incorrect predictions. Interpretability is particularly crucial to ML for clinical diagnosis as the consumers must gain necessary sense of security and trust from firm grounds or convincing interpretations. In this work, we propose a tensor-network (TN)-ML method to reliably predict lung cancer patients and their stages via screening Raman spectra data of Volatile organic compounds (VOCs) in exhaled breath, which are generally suitable as biomarkers and are considered to be an ideal way for non-invasive lung cancer screening. The prediction of TN-ML is based on the mutual distances of the breath samples mapped to the quantum Hilbert space. Thanks to the quantum probabilistic interpretation, the certainty of the predictions can be quantitatively characterized. The accuracy of the samples with high certainty is almost 100$\%$. The incorrectly-classified samples exhibit obviously lower certainty, and thus can be decipherably identified as anomalies, which will be handled by human experts to guarantee high reliability. Our work sheds light on shifting the ``AI for biomedical sciences'' from the conventional non-interpretable ML schemes to the interpretable human-ML interactive approaches, for the purpose of high accuracy and reliability.

Deep Machine Learning Reconstructing Lattice Topology with Strong Thermal Fluctuations

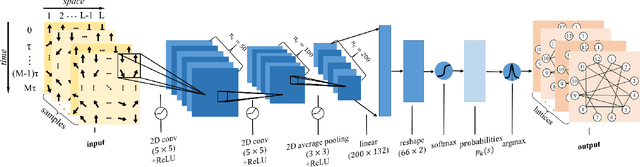
Applying artificial intelligence to scientific problems (namely AI for science) is currently under hot debate. However, the scientific problems differ much from the conventional ones with images, texts, and etc., where new challenges emerges with the unbalanced scientific data and complicated effects from the physical setups. In this work, we demonstrate the validity of the deep convolutional neural network (CNN) on reconstructing the lattice topology (i.e., spin connectivities) in the presence of strong thermal fluctuations and unbalanced data. Taking the kinetic Ising model with Glauber dynamics as an example, the CNN maps the time-dependent local magnetic momenta (a single-node feature) evolved from a specific initial configuration (dubbed as an evolution instance) to the probabilities of the presences of the possible couplings. Our scheme distinguishes from the previous ones that might require the knowledge on the node dynamics, the responses from perturbations, or the evaluations of statistic quantities such as correlations or transfer entropy from many evolution instances. The fine tuning avoids the "barren plateau" caused by the strong thermal fluctuations at high temperatures. Accurate reconstructions can be made where the thermal fluctuations dominate over the correlations and consequently the statistic methods in general fail. Meanwhile, we unveil the generalization of CNN on dealing with the instances evolved from the unlearnt initial spin configurations and those with the unlearnt lattices. We raise an open question on the learning with unbalanced data in the nearly "double-exponentially" large sample space.

Unsupervised Recognition of Informative Features via Tensor Network Machine Learning and Quantum Entanglement Variations

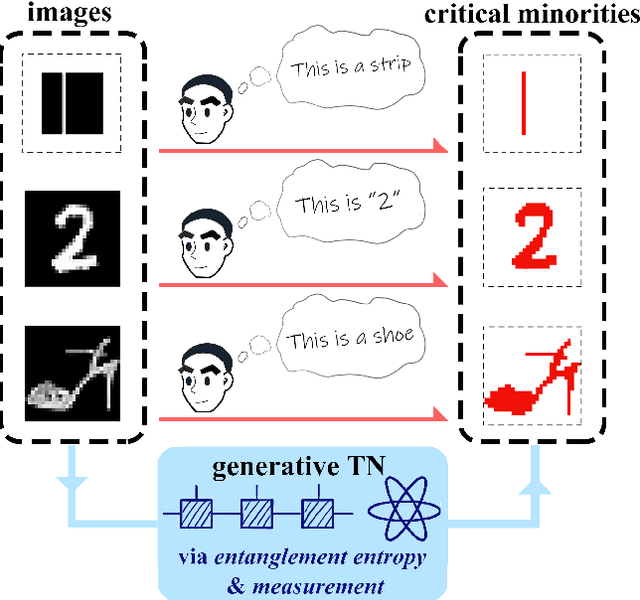
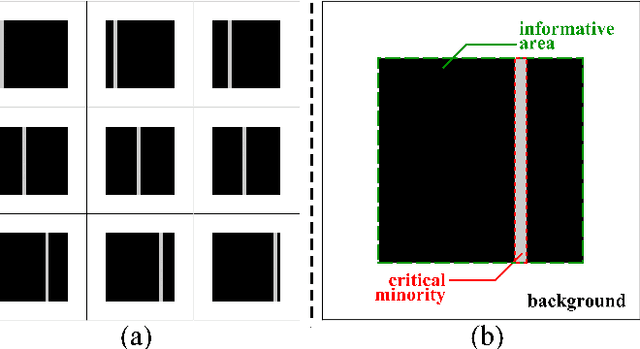
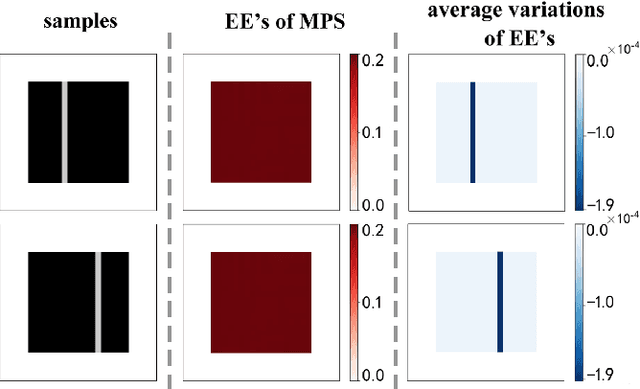
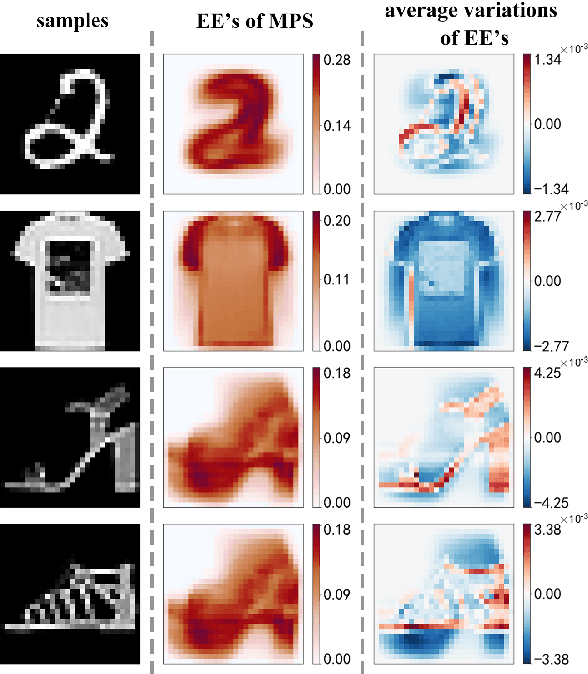
Given an image of a white shoe drawn on a blackboard, how are the white pixels deemed (say by human minds) to be informative for recognizing the shoe without any labeling information on the pixels? Here we investigate such a "white shoe" recognition problem from the perspective of tensor network (TN) machine learning and quantum entanglement. Utilizing a generative TN that captures the probability distribution of the features as quantum amplitudes, we propose an unsupervised recognition scheme of informative features with the variations of entanglement entropy (EE) caused by designed measurements. In this way, a given sample, where the values of its features are statistically meaningless, is mapped to the variations of EE that are statistically meaningful. We show that the EE variations identify the features that are critical to recognize this specific sample, and the EE itself reveals the information distribution from the TN model. The signs of the variations further reveal the entanglement structures among the features. We test the validity of our scheme on a toy dataset of strip images, the MNIST dataset of hand-drawn digits, and the fashion-MNIST dataset of the pictures of fashion articles. Our scheme opens the avenue to the quantum-inspired and interpreted unsupervised learning and could be applied to, e.g., image segmentation and object detection.

Circuit encapsulation for efficient quantum computing based on controlled many-body dynamics

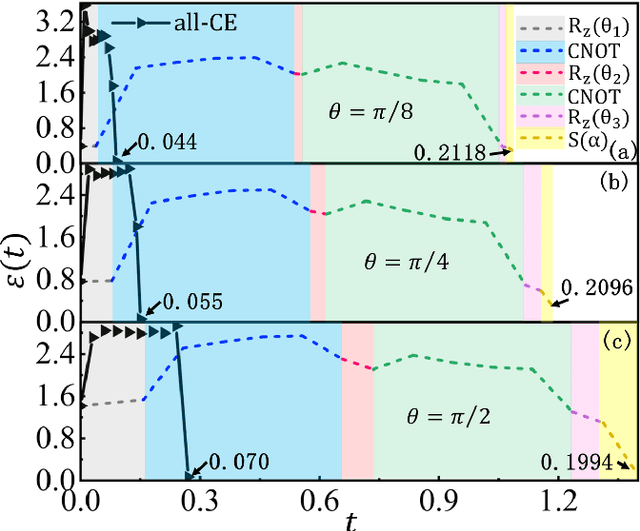
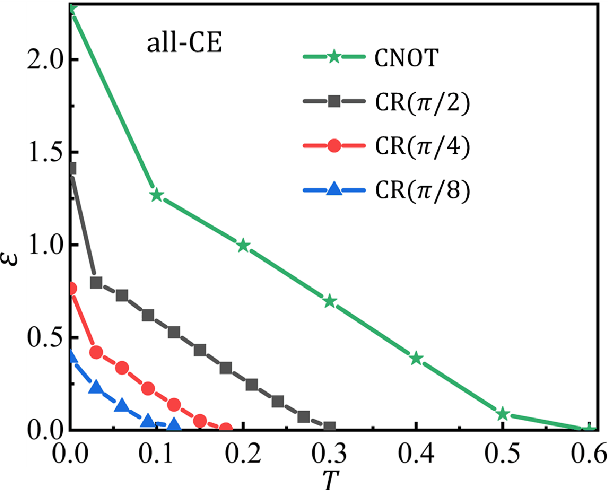
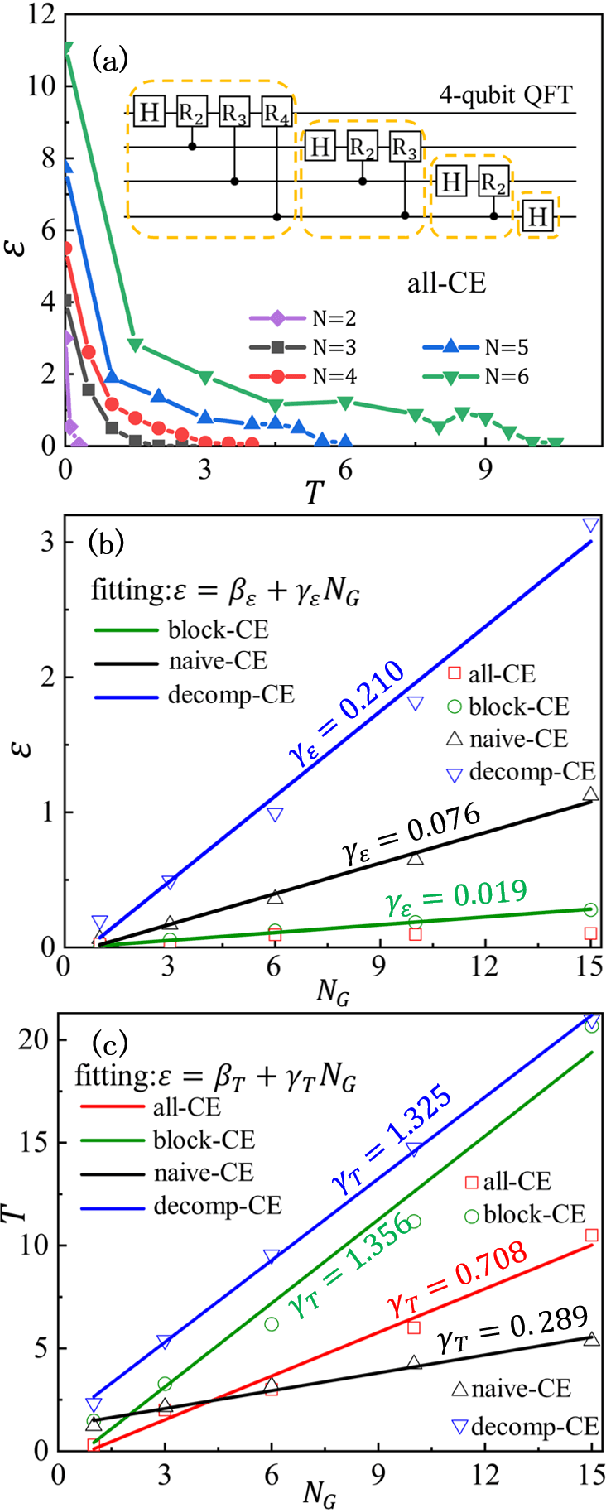
Controlling the time evolution of interacting spin systems is an important approach of implementing quantum computing. Different from the approaches by compiling the circuits into the product of multiple elementary gates, we here propose the quantum circuit encapsulation (QCE), where we encapsulate the circuits into different parts, and optimize the magnetic fields to realize the unitary transformation of each part by the time evolution. The QCE is demonstrated to possess well-controlled error and time cost, which avoids the error accumulations by aiming at finding the shortest path directly to the target unitary. We test four different encapsulation ways to realize the multi-qubit quantum Fourier transformations by controlling the time evolution of the quantum Ising chain. The scaling behaviors of the time costs and errors against the number of two-qubit controlled gates are demonstrated. The QCE provides an alternative compiling scheme that translates the circuits into a physically-executable form based on the quantum many-body dynamics, where the key issue becomes the encapsulation way to balance between the efficiency and flexibility.

Non-parametric Active Learning and Rate Reduction in Many-body Hilbert Space with Rescaled Logarithmic Fidelity

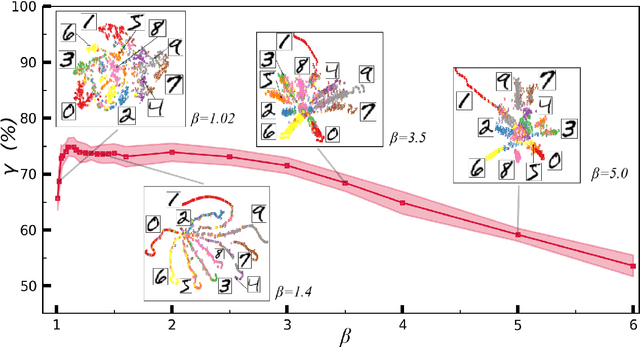
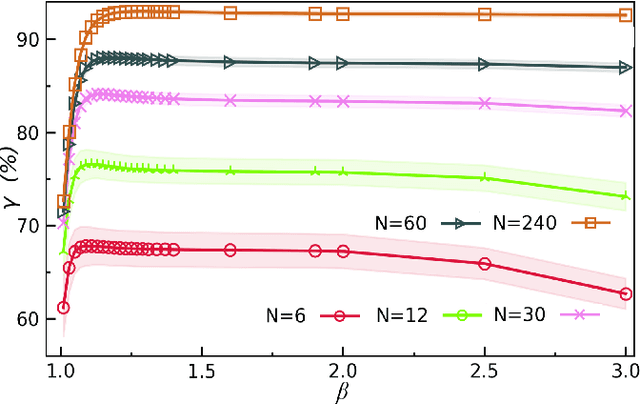
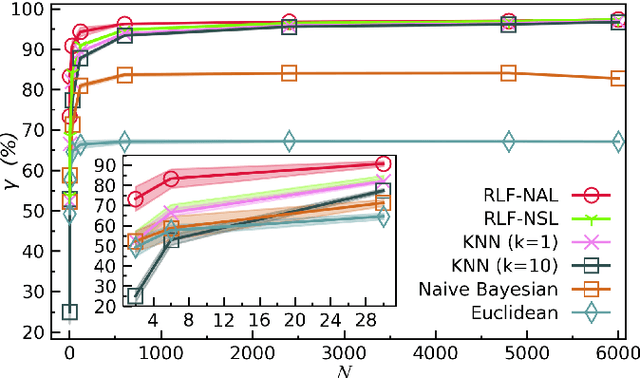
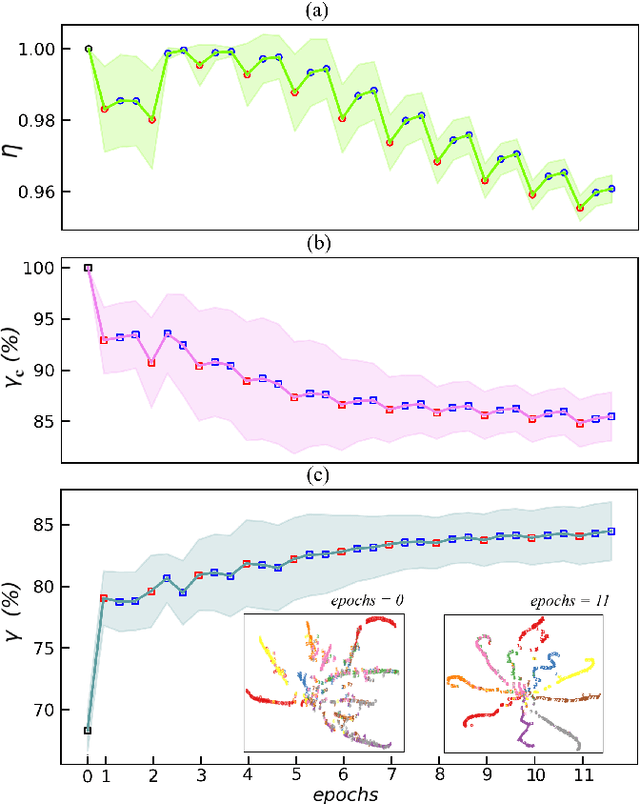
In quantum and quantum-inspired machine learning, the very first step is to embed the data in quantum space known as Hilbert space. Developing quantum kernel function (QKF), which defines the distances among the samples in the Hilbert space, belongs to the fundamental topics for machine learning. In this work, we propose the rescaled logarithmic fidelity (RLF) and a non-parametric active learning in the quantum space, which we name as RLF-NAL. The rescaling takes advantage of the non-linearity of the kernel to tune the mutual distances of samples in the Hilbert space, and meanwhile avoids the exponentially-small fidelities between quantum many-qubit states. We compare RLF-NAL with several well-known non-parametric algorithms including naive Bayes classifiers, $k$-nearest neighbors, and spectral clustering. Our method exhibits excellent accuracy particularly for the unsupervised case with no labeled samples and the few-shot cases with small numbers of labeled samples. With the visualizations by t-SNE, our results imply that the machine learning in the Hilbert space complies with the principles of maximal coding rate reduction, where the low-dimensional data exhibit within-class compressibility, between-class discrimination, and overall diversity. Our proposals can be applied to other quantum and quantum-inspired machine learning, including the methods using the parametric models such as tensor networks, quantum circuits, and quantum neural networks.