Circuit encapsulation for efficient quantum computing based on controlled many-body dynamics

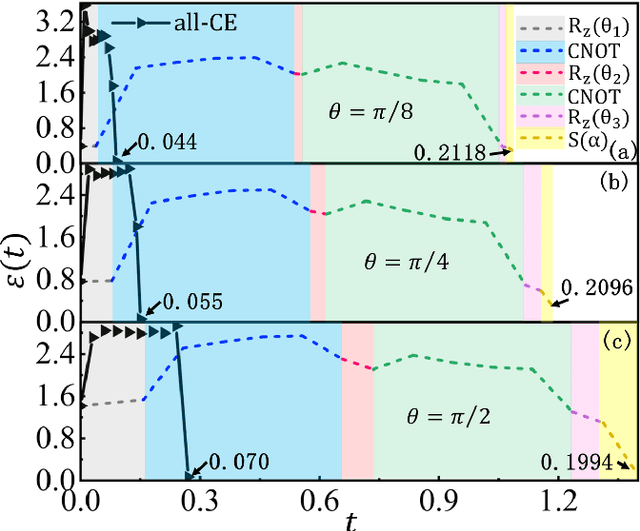
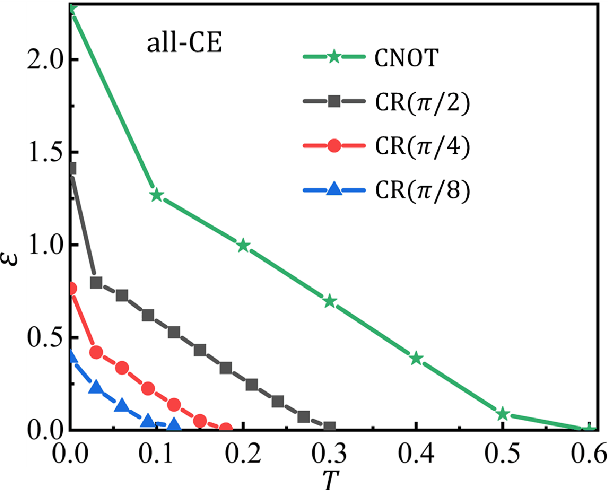
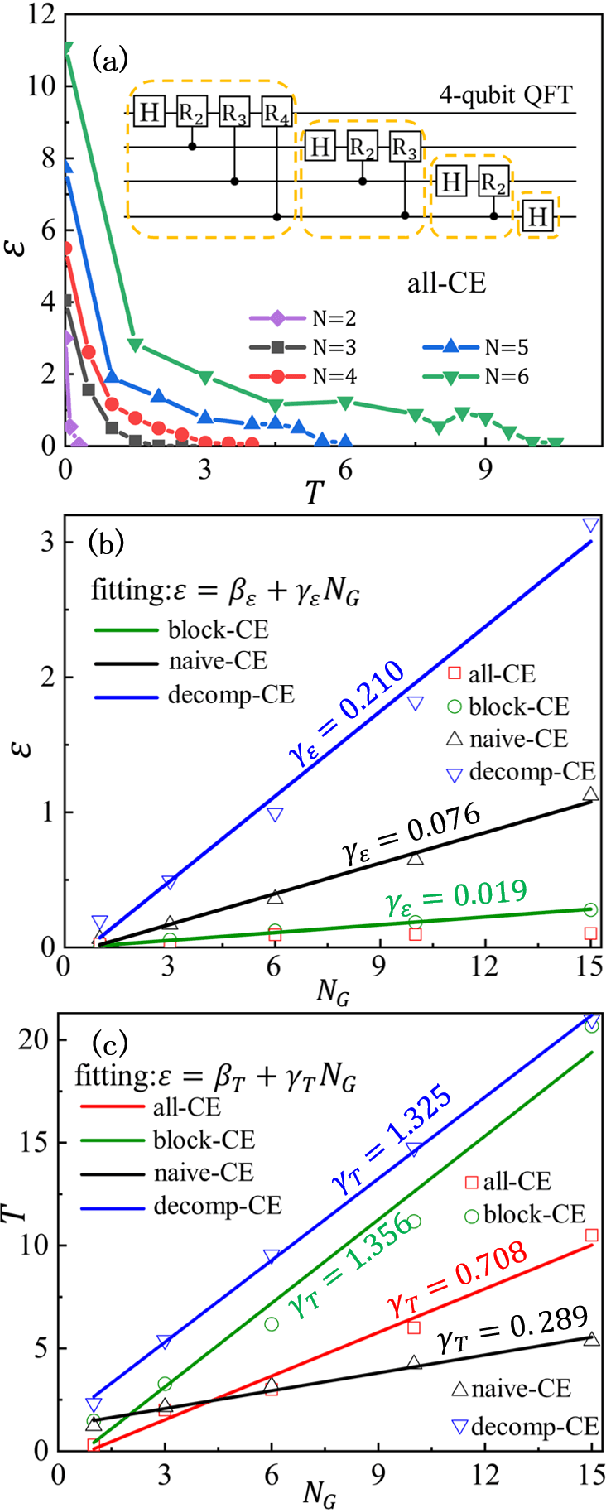
Controlling the time evolution of interacting spin systems is an important approach of implementing quantum computing. Different from the approaches by compiling the circuits into the product of multiple elementary gates, we here propose the quantum circuit encapsulation (QCE), where we encapsulate the circuits into different parts, and optimize the magnetic fields to realize the unitary transformation of each part by the time evolution. The QCE is demonstrated to possess well-controlled error and time cost, which avoids the error accumulations by aiming at finding the shortest path directly to the target unitary. We test four different encapsulation ways to realize the multi-qubit quantum Fourier transformations by controlling the time evolution of the quantum Ising chain. The scaling behaviors of the time costs and errors against the number of two-qubit controlled gates are demonstrated. The QCE provides an alternative compiling scheme that translates the circuits into a physically-executable form based on the quantum many-body dynamics, where the key issue becomes the encapsulation way to balance between the efficiency and flexibility.