Compressing neural network by tensor network with exponentially fewer variational parameters

Neural network (NN) designed for challenging machine learning tasks is in general a highly nonlinear mapping that contains massive variational parameters. High complexity of NN, if unbounded or unconstrained, might unpredictably cause severe issues including over-fitting, loss of generalization power, and unbearable cost of hardware. In this work, we propose a general compression scheme that significantly reduces the variational parameters of NN by encoding them to multi-layer tensor networks (TN's) that contain exponentially-fewer free parameters. Superior compression performance of our scheme is demonstrated on several widely-recognized NN's (FC-2, LeNet-5, and VGG-16) and datasets (MNIST and CIFAR-10), surpassing the state-of-the-art method based on shallow tensor networks. For instance, about 10 million parameters in the three convolutional layers of VGG-16 are compressed in TN's with just $632$ parameters, while the testing accuracy on CIFAR-10 is surprisingly improved from $81.14\%$ by the original NN to $84.36\%$ after compression. Our work suggests TN as an exceptionally efficient mathematical structure for representing the variational parameters of NN's, which superiorly exploits the compressibility than the simple multi-way arrays.

Circuit encapsulation for efficient quantum computing based on controlled many-body dynamics

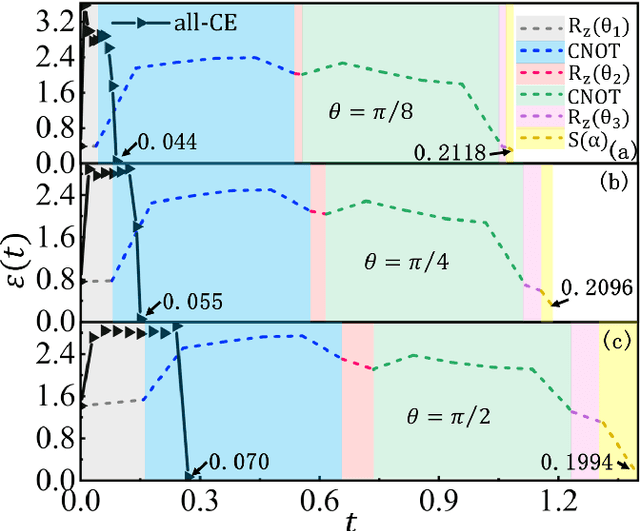
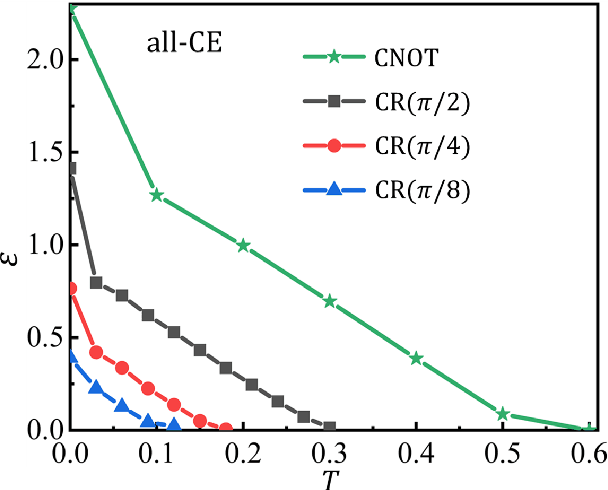
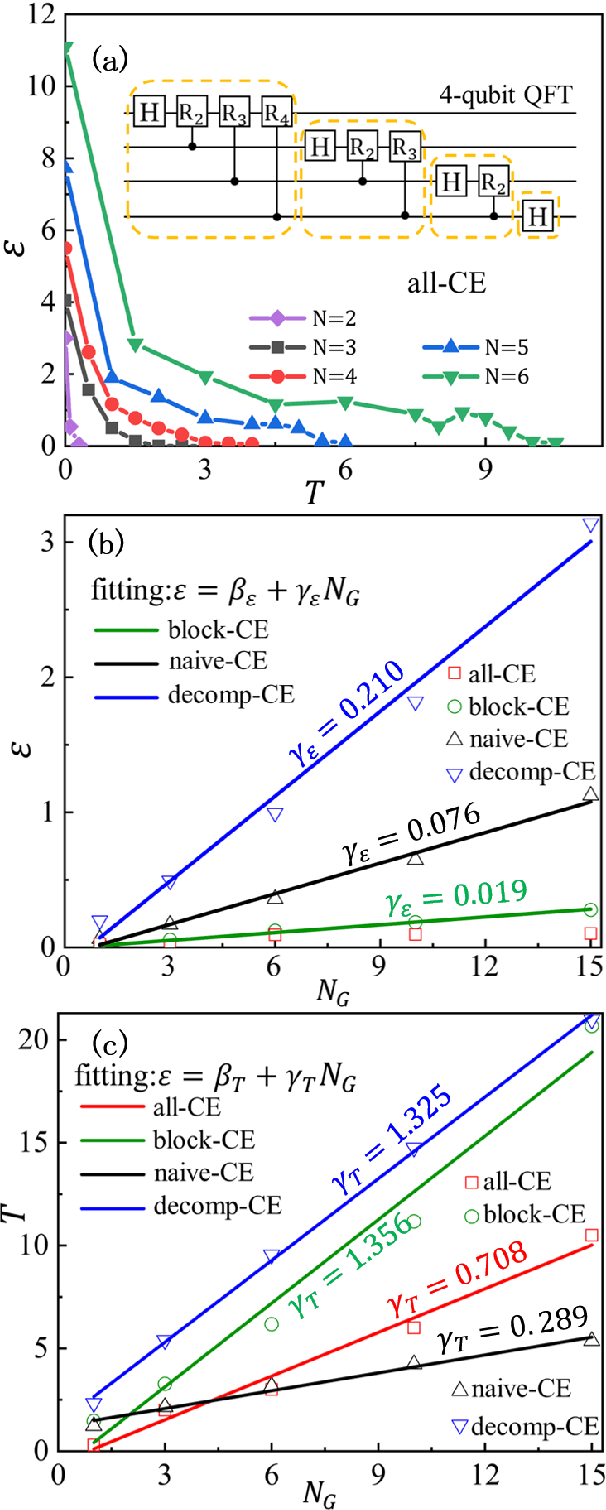
Controlling the time evolution of interacting spin systems is an important approach of implementing quantum computing. Different from the approaches by compiling the circuits into the product of multiple elementary gates, we here propose the quantum circuit encapsulation (QCE), where we encapsulate the circuits into different parts, and optimize the magnetic fields to realize the unitary transformation of each part by the time evolution. The QCE is demonstrated to possess well-controlled error and time cost, which avoids the error accumulations by aiming at finding the shortest path directly to the target unitary. We test four different encapsulation ways to realize the multi-qubit quantum Fourier transformations by controlling the time evolution of the quantum Ising chain. The scaling behaviors of the time costs and errors against the number of two-qubit controlled gates are demonstrated. The QCE provides an alternative compiling scheme that translates the circuits into a physically-executable form based on the quantum many-body dynamics, where the key issue becomes the encapsulation way to balance between the efficiency and flexibility.

Predicting Quantum Potentials by Deep Neural Network and Metropolis Sampling

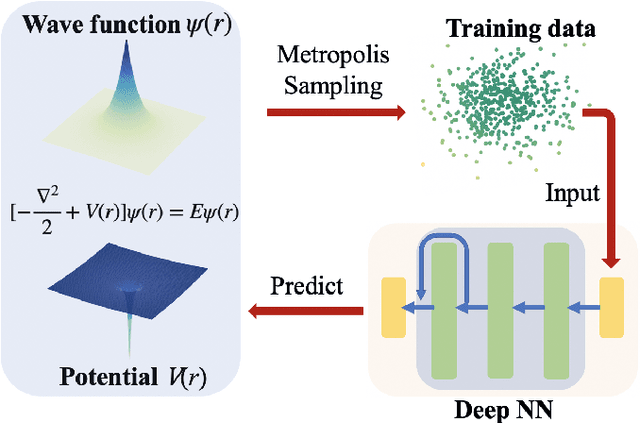
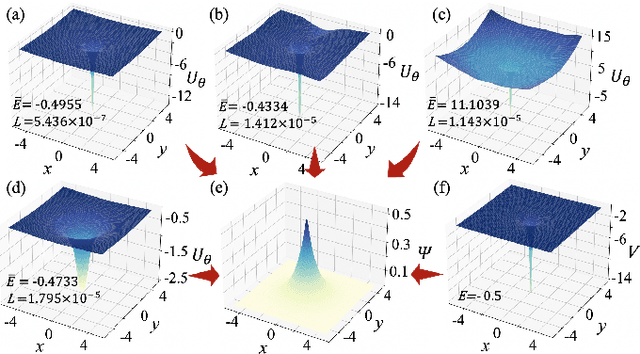
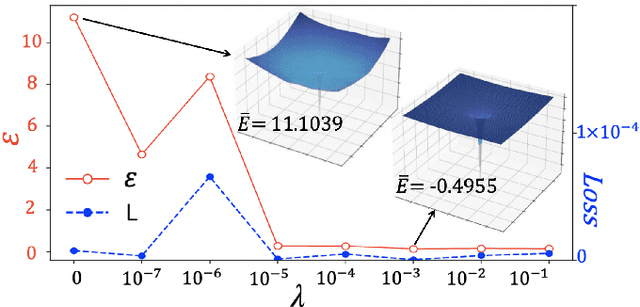
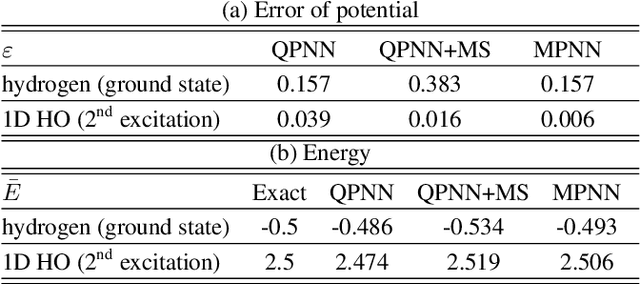
The hybridizations of machine learning and quantum physics have caused essential impacts to the methodology in both fields. Inspired by quantum potential neural network, we here propose to solve the potential in the Schrodinger equation provided the eigenstate, by combining Metropolis sampling with deep neural network, which we dub as Metropolis potential neural network (MPNN). A loss function is proposed to explicitly involve the energy in the optimization for its accurate evaluation. Benchmarking on the harmonic oscillator and hydrogen atom, MPNN shows excellent accuracy and stability on predicting not just the potential to satisfy the Schrodinger equation, but also the eigen-energy. Our proposal could be potentially applied to the ab-initio simulations, and to inversely solving other partial differential equations in physics and beyond.

Preparation of Many-body Ground States by Time Evolution with Variational Microscopic Magnetic Fields and Incomplete Interactions

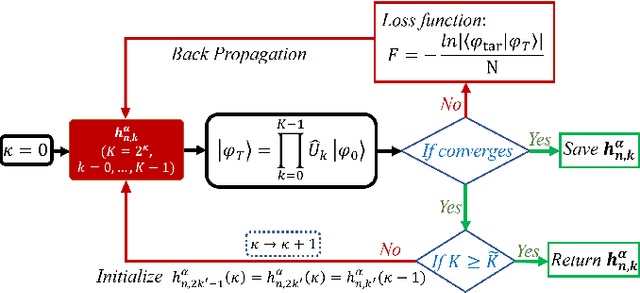
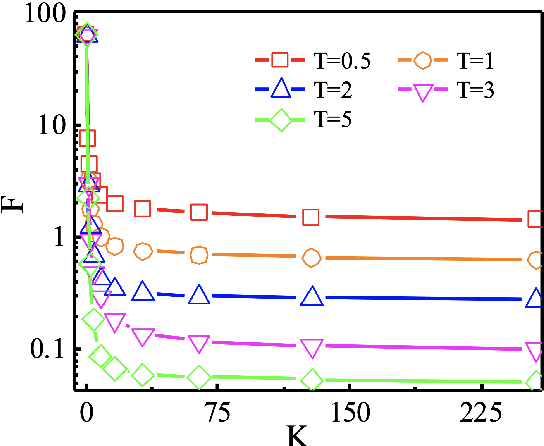
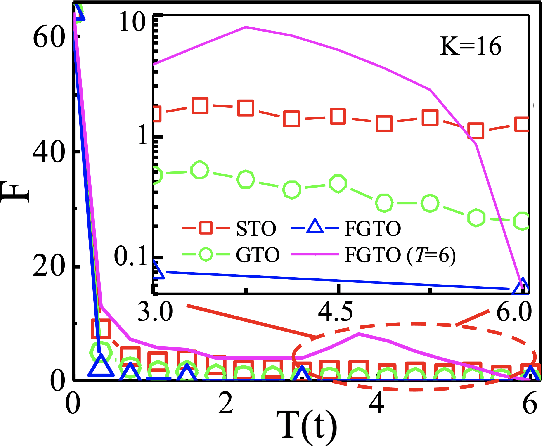
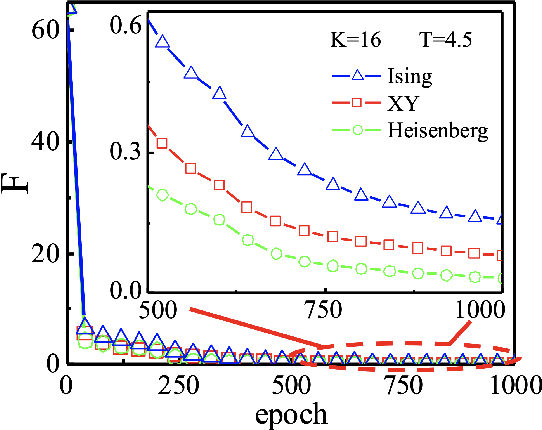
State preparation is of fundamental importance in quantum physics, which can be realized by constructing the quantum circuit as a unitary that transforms the initial state to the target, or implementing a quantum control protocol to evolve to the target state with a designed Hamiltonian. In this work, we study the latter on quantum many-body systems by the time evolution with fixed couplings and variational magnetic fields. In specific, we consider to prepare the ground states of the Hamiltonians containing certain interactions that are missing in the Hamiltonians for the time evolution. An optimization method is proposed to optimize the magnetic fields by "fine-graining" the discretization of time, in order to gain high precision and stability. The back propagation technique is utilized to obtain the gradients of the fields against the logarithmic fidelity. Our method is tested on preparing the ground state of Heisenberg chain with the time evolution by the XY and Ising interactions, and its performance surpasses two baseline methods that use local and global optimization strategies, respectively. Our work can be applied and generalized to other quantum models such as those defined on higher dimensional lattices. It enlightens to reduce the complexity of the required interactions for implementing quantum control or other tasks in quantum information and computation by means of optimizing the magnetic fields.

Automatically Differentiable Quantum Circuit for Many-qubit State Preparation

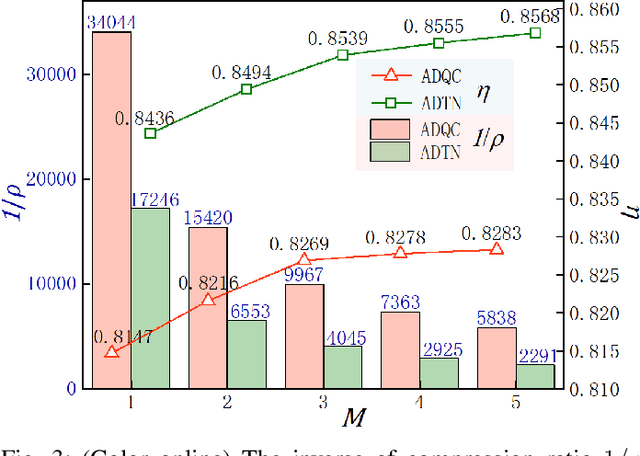
Constructing quantum circuits for efficient state preparation belongs to the central topics in the field of quantum information and computation. As the number of qubits grows fast, methods to derive large-scale quantum circuits are strongly desired. In this work, we propose the automatically differentiable quantum circuit (ADQC) approach to efficiently prepare arbitrary quantum many-qubit states. A key ingredient is to introduce the latent gates whose decompositions give the unitary gates that form the quantum circuit. The circuit is optimized by updating the latent gates using back propagation to minimize the distance between the evolved and target states. Taking the ground states of quantum lattice models and random matrix product states as examples, with the number of qubits where processing the full coefficients is unlikely, ADQC obtains high fidelities with small numbers of layers $N_L \sim O(1)$. Superior accuracy is reached compared with the existing state-preparation approach based on the matrix product disentangler. The parameter complexity of MPS can be significantly reduced by ADQC with the compression ratio $r \sim O(10^{-3})$. Our work sheds light on the "intelligent construction" of quantum circuits for many-qubit systems by combining with the machine learning methods.