Compressing neural network by tensor network with exponentially fewer variational parameters

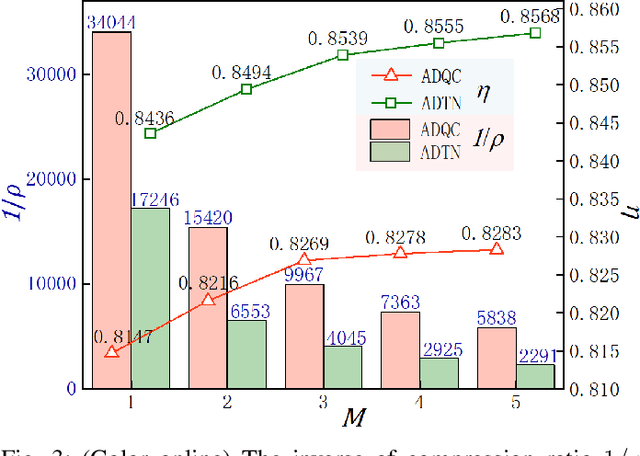
Neural network (NN) designed for challenging machine learning tasks is in general a highly nonlinear mapping that contains massive variational parameters. High complexity of NN, if unbounded or unconstrained, might unpredictably cause severe issues including over-fitting, loss of generalization power, and unbearable cost of hardware. In this work, we propose a general compression scheme that significantly reduces the variational parameters of NN by encoding them to multi-layer tensor networks (TN's) that contain exponentially-fewer free parameters. Superior compression performance of our scheme is demonstrated on several widely-recognized NN's (FC-2, LeNet-5, and VGG-16) and datasets (MNIST and CIFAR-10), surpassing the state-of-the-art method based on shallow tensor networks. For instance, about 10 million parameters in the three convolutional layers of VGG-16 are compressed in TN's with just $632$ parameters, while the testing accuracy on CIFAR-10 is surprisingly improved from $81.14\%$ by the original NN to $84.36\%$ after compression. Our work suggests TN as an exceptionally efficient mathematical structure for representing the variational parameters of NN's, which superiorly exploits the compressibility than the simple multi-way arrays.