Deep Machine Learning Reconstructing Lattice Topology with Strong Thermal Fluctuations

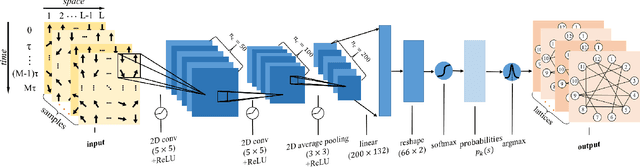
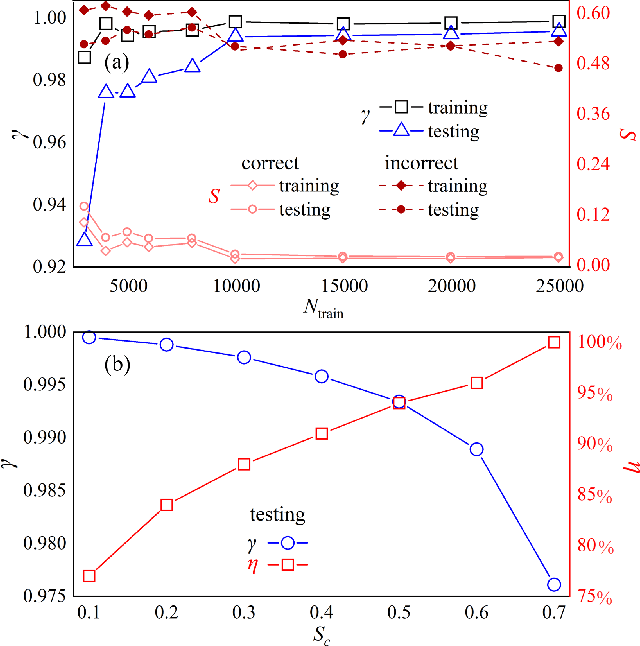
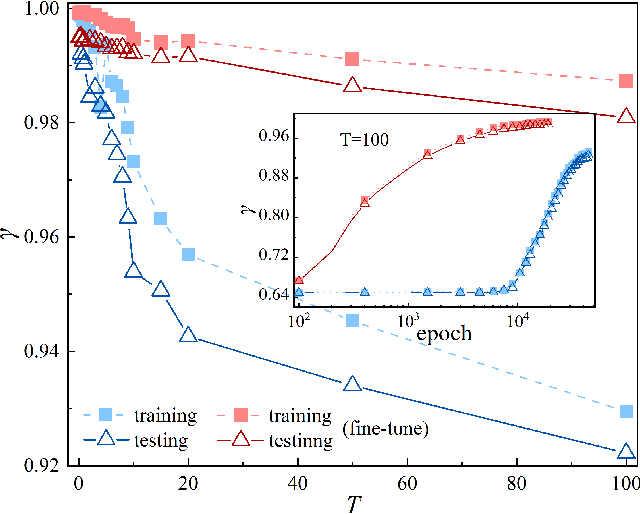
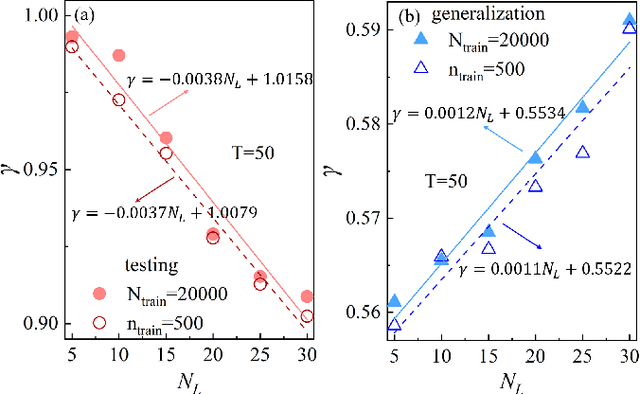
Applying artificial intelligence to scientific problems (namely AI for science) is currently under hot debate. However, the scientific problems differ much from the conventional ones with images, texts, and etc., where new challenges emerges with the unbalanced scientific data and complicated effects from the physical setups. In this work, we demonstrate the validity of the deep convolutional neural network (CNN) on reconstructing the lattice topology (i.e., spin connectivities) in the presence of strong thermal fluctuations and unbalanced data. Taking the kinetic Ising model with Glauber dynamics as an example, the CNN maps the time-dependent local magnetic momenta (a single-node feature) evolved from a specific initial configuration (dubbed as an evolution instance) to the probabilities of the presences of the possible couplings. Our scheme distinguishes from the previous ones that might require the knowledge on the node dynamics, the responses from perturbations, or the evaluations of statistic quantities such as correlations or transfer entropy from many evolution instances. The fine tuning avoids the "barren plateau" caused by the strong thermal fluctuations at high temperatures. Accurate reconstructions can be made where the thermal fluctuations dominate over the correlations and consequently the statistic methods in general fail. Meanwhile, we unveil the generalization of CNN on dealing with the instances evolved from the unlearnt initial spin configurations and those with the unlearnt lattices. We raise an open question on the learning with unbalanced data in the nearly "double-exponentially" large sample space.

Predicting Quantum Potentials by Deep Neural Network and Metropolis Sampling

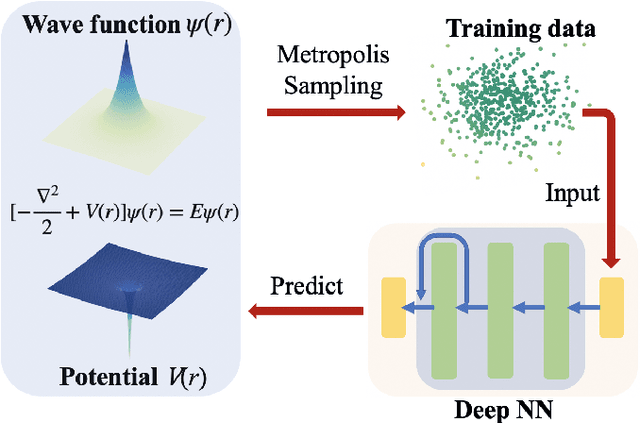
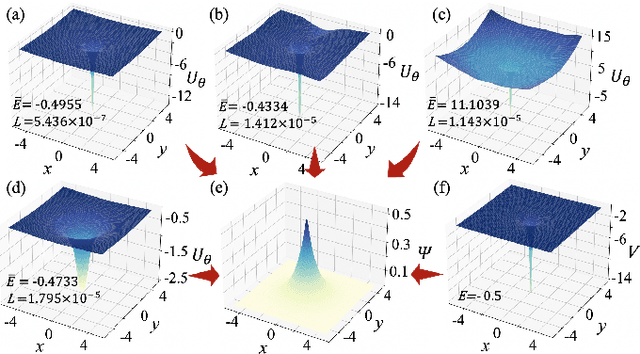
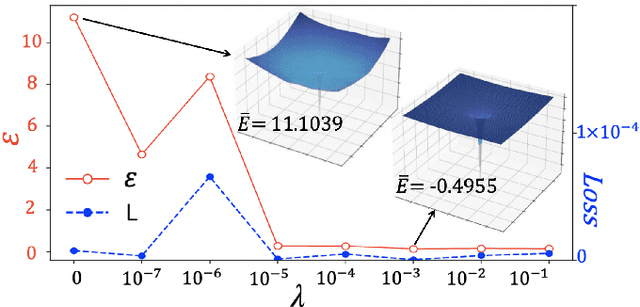
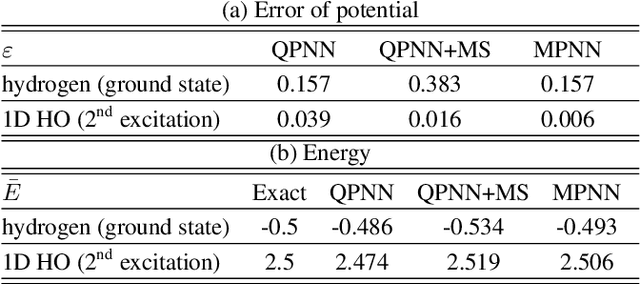
The hybridizations of machine learning and quantum physics have caused essential impacts to the methodology in both fields. Inspired by quantum potential neural network, we here propose to solve the potential in the Schrodinger equation provided the eigenstate, by combining Metropolis sampling with deep neural network, which we dub as Metropolis potential neural network (MPNN). A loss function is proposed to explicitly involve the energy in the optimization for its accurate evaluation. Benchmarking on the harmonic oscillator and hydrogen atom, MPNN shows excellent accuracy and stability on predicting not just the potential to satisfy the Schrodinger equation, but also the eigen-energy. Our proposal could be potentially applied to the ab-initio simulations, and to inversely solving other partial differential equations in physics and beyond.